Posición sobre a traxectoria
Até agora, para indicar a posición dun móbil, temos usado as coordenadas do punto que ocupa (que coinciden coas compoñentes do vector de posición). Pero imaxina que viaxas nun tren, indicarías a posición mediante coordenadas? Non te sería máis sinxelo indicar o punto quilométrico en que te encontras enriba da vía contado a partir dunha estación de tren determinada?
Efectivamente, por veces é máis sinxelo indicar a posición contando desde unha orixe sobre a traxectoria. A esta magnitude a chamamos posición sobre a traxectoria e a representamos mediante un "s" ou, por veces, mediante un "e". Cando se traballa con esta magnitude escalar a relacionamos con outras tamén escalares: a rapidez e a chamada aceleración tanxencial. O espazo percorrido sobre a traxectoria será a resta entre aposición que ocupa o móbil e a considerada inicial.
Na simulación tes un movemento que non é rectilíneo pero cuxa rapidez é constante. Decátate da representación da posición sobre a traxectoria e das coordenadas x e y.
A rapidez instantánea coincide co módulo do vector velocidade instantánea. Nun movemento uniforme, a rapidez instantánea a podemos calcular así:
![]()
MCU
Como o seu nome indica, un movemento circular é un movemento que ten unha traxectoria circular e, se é uniforme, a súa rapidez será constante.
Como indicamos no punto anterior, neste caso é máis sinxelo estudar o movemento escalarmente que con vectores. Podemos definir un punto coma orixe de posicións e, a partir del contar as distancias enriba da propia traxectoria.
Observa a simulación e as diferentes representacións da posición sobre a traxectoria, as X, as Y e o ángulo en función do tempo.
Un movemento circular e uniforme non ten aceleración na dirección do movemento (chamada aceleración tanxencial). Pero si que ten unha aceleración que obriga ao vector velocidade (que é sempre perpendicular á traxectoria e dirixida cara o centro da circunferencia) a cambiar continuamente de dirección; esta aceleración recibe o nome de aceleración centrípeta (ou normal) e se pode calcular dividindo a rapidez ao cadrado polo raio da circunferencia:
![]()
Magnitudes angulares
Terás visto na simulación anterior que tamén sería sinxelo estudar o movemento circular usando o ángulo α, xa que hay unha relación entre a posición sobre a traxectoria (mira que é o arco da cincunferencia), o raio e o ángulo:
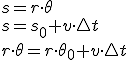
Tamén podemos definir a velocidade angular nun MCU como a variación do ángulo dividida polo tempo que tarda en darse esa variación, e recordando a expresión da rapidez en función do espazo percorrido:
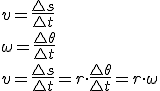
Podemos pois deixar unha ecuación angular:
![]()
No sistema internacional de unidades, o ángulo o mediremos en radiáns e a velocidade angular en radiáns por segundo (rad/s).
MCUA
Moitos autores prefiren chamar a este movemento Movemento Circular Uniformemente Variado (MCUV), debido a que nun Movemento Circular Uniforme existe aceleración (a aceleración centrípeta) e a denominación anterior pode levar a confusións.
Independentemente de como decidamos chamar a este movemento (MCUA ou MCUV) neste tipo de movemento a rapidez varía de forma lineal co tempo polo tanto, alén da correspondente aceleración centrípeta, teremos que falar doutra aceleración que chamaremos tanxencial. A aceleración tanxencial calcúlase dividindo a variación sufrida pola rapidez entre o tempo que se tarda en realizar esta variación:
![]()
Se o intervalo de medición do tempo é moi pequeno, falamos de aceleración tanxencial instantánea.
Magnitudes angulares
Podemos definir tamén a chamada aceleración angular como a variación producida na velocidade angular dividida polo tempo que tarda en producirse:
![]()
A súa unidade ni sistema internacional é o radián por segundo ao cadrado (rad/s2). Esta aceleración será instantánea se o intervalo temporal na medición é moi pequeno.
Existe unha relación entre a aceleración tanxencial, o raio da circunferencia e a aceleración angular:
![]()
Podemos, pois, escribir as ecuacións da posición sobre a traxectoria en función do tempo ou usar as magnitudes angulares:
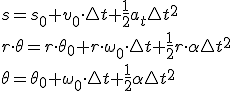
Na simulación podemos ver como varían as magnitudes angulares en función do tempo.