Como se viu no apartado anterior, as táboas da normal estándar dannos a probabilidade de que unha variable aleatoria con distribución N(0,1) tome un valor menor ou igual a un número "a" positivo, pero hai máis casos. Lembra que a probabilidade é a área dunha determinada rexión do plano.
Vexamos a continuación todos os posibles casos ao calcular a probabilidade dunha N(0, 1).
- P(Z ≥ a): Probabilidade de que Z sexa maior ou igual a "a"
- Se a > 0: P(Z ≥ a) = 1 - P(X ≤ a)
- Se a < 0: P(Z ≥ a) = P(X ≤ -a) (Obsérvese que si a<0 entón -a é un número positivo).
- Exemplo 1
-
Calcular P(Z > 1.28).
P(Z > 1.28) = 1 - P(Z ≤ 1.28) = 1 - 0.8997 = 0.1003
Gráficamente
Zona azul = P(Z > 1.28)
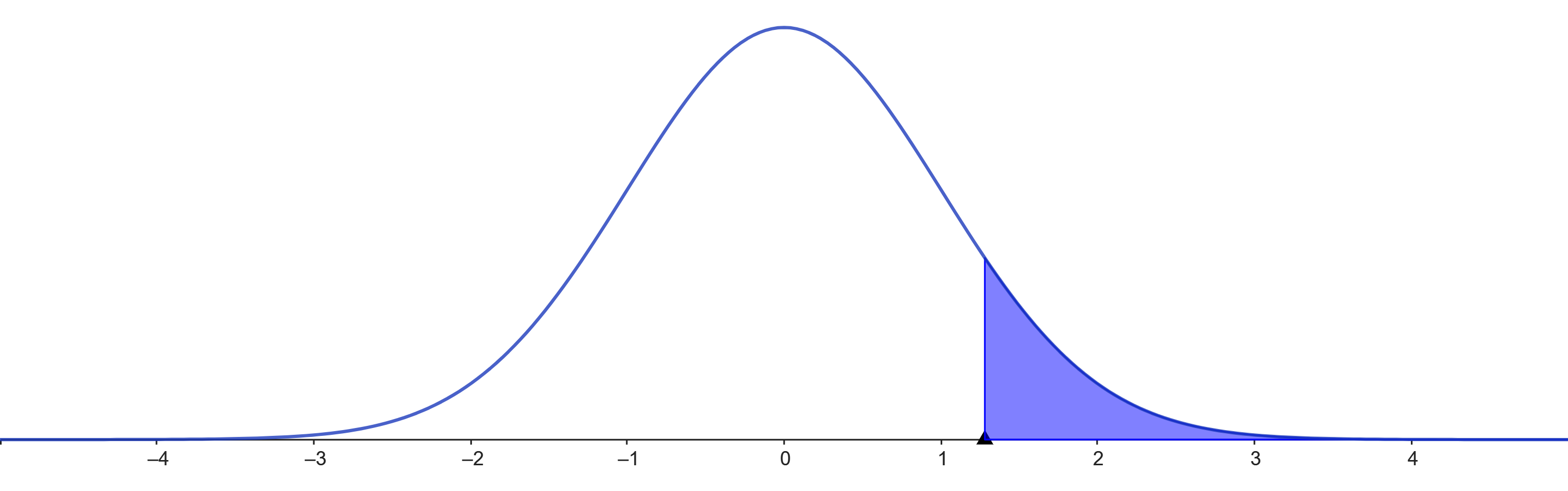
Zona azul = P(Z ≤ 1,28) 
- Exemplo 2
-
Calcular P(Z > -1.28).
Solución
P(Z > -1.28) = P( Z ≤ 1.28) = 0.8997
Gráficamente
Zona azul = P(Z > -1.28)
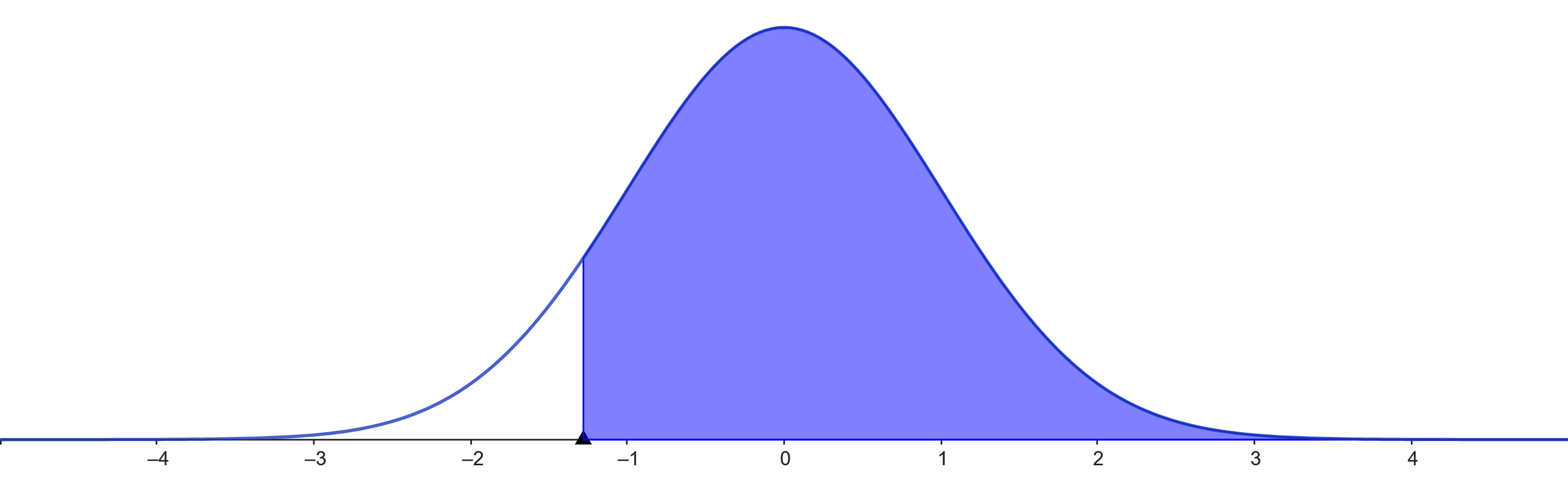
Zona azul = P( Z ≤ 1.28)

- P(Z ≤ a): Probabilidade de que Z sexa menor ou igual a "a"
- Se a > 0: Búscase directamente na táboa
- Se a < 0: P(Z ≤ a) = P(Z ≥ -a) = 1- P(Z ≤ -a)
- Exemplo 3
-
Calcular P(Z < -1.28).
Solución
P(Z < -1.28) = P(Z > 1.28) = 1- P(Z ≤ 1.28) = 1 - 0.8997 = 0.1003
Gráficamente
Zona azul = P(Z < -1.28)

Zona azul = P(Z > 1.28)

Zona azul = P(Z ≤ 1.28)

- P(a < Z < b): Probabilidade de que Z estea entre dous valores "a" e "b
- Se a e b positivos: P(Z ≤ b) - P(Z ≤ a)
- Se a e b negativos: P(Z ≤ -a) - P(Z ≤ -b)
- Se a é negativo e b positivo: P(Z ≤ b) - [1- P(Z ≤ -a)]
- Exemplo 4
-
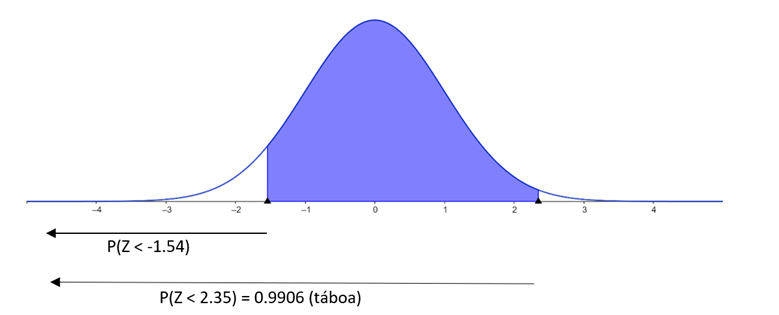
Calcular P(1.54 < Z < 2.35)
Solución
P(1.54 < Z < 2.35) = P(Z < 2.35) - P(Z < 1.54) = 0.9906 - 0.9382 = 0.0524
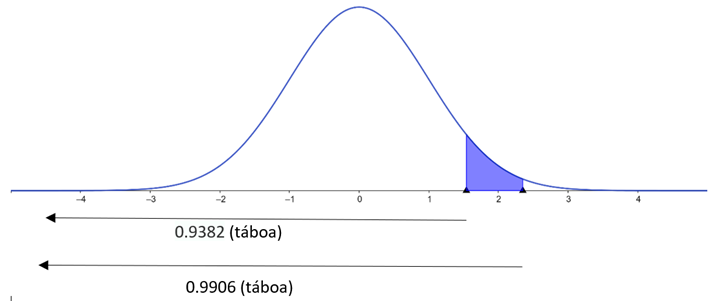
Gráficamente
Zona azul = P(Z < 2.35)

Zona azul = P(Z < 1.54)

Zona azul = P(1.54 < Z < 2.35)
- Exemplo 5
-
Calcular P(-2.35 < Z < -1.54 )
Solución
P(-2.35 < Z < -1.54 ) = P(1.54 < Z < 2.35) = 0.9906 - 0.9382 = 0.0524
Gráficamente
Zona azul = P(-2.35 < Z < -1.54 )
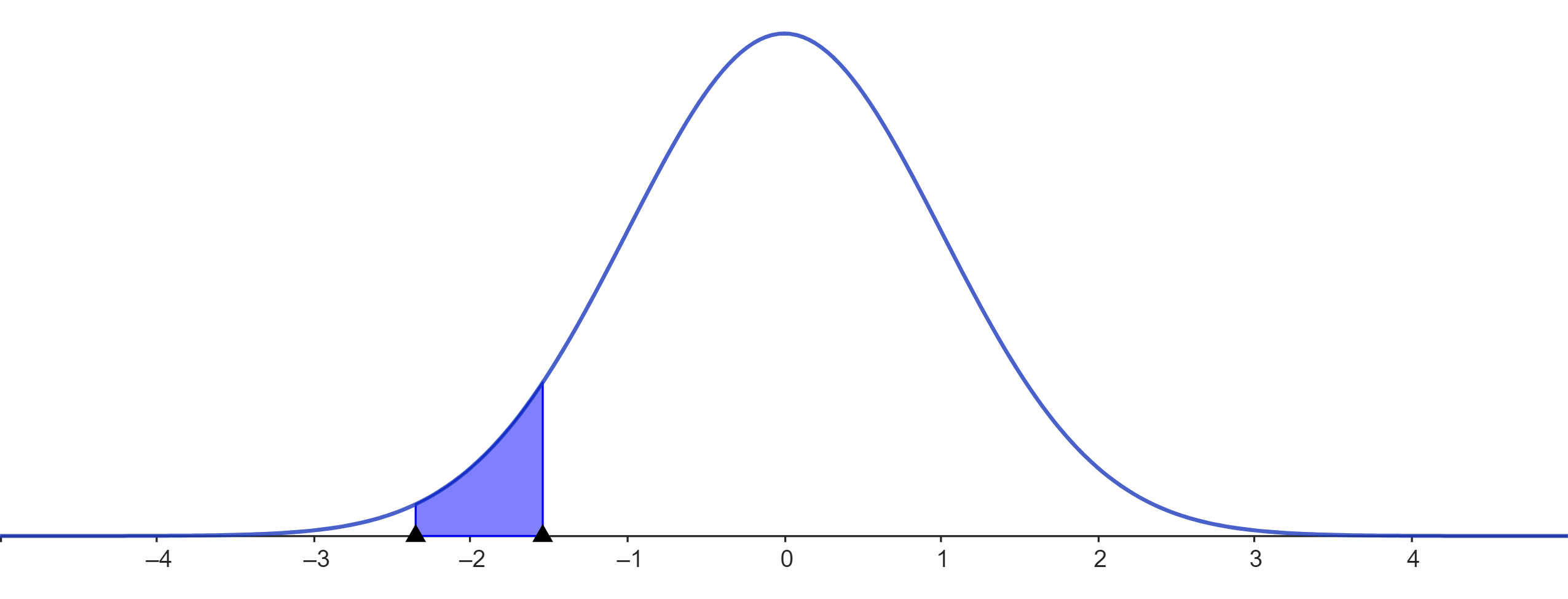
Zona azul = P(1.54 < Z < 2.35)
A partir de aquí, ver o exemplo 5
- Exemplo 6
-
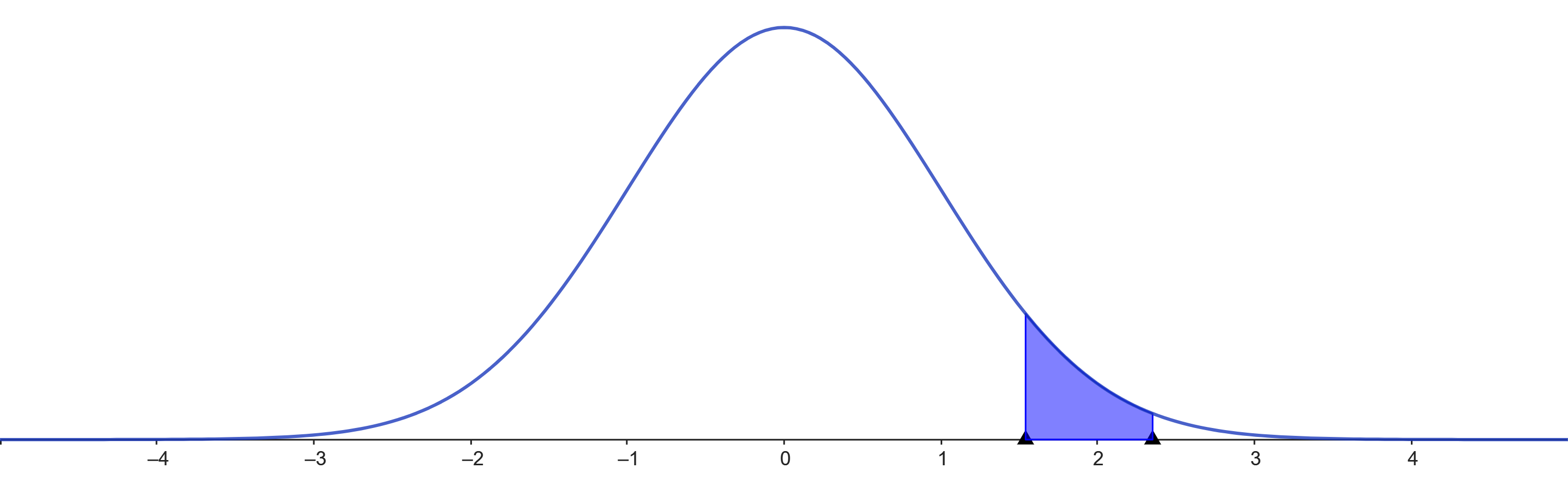
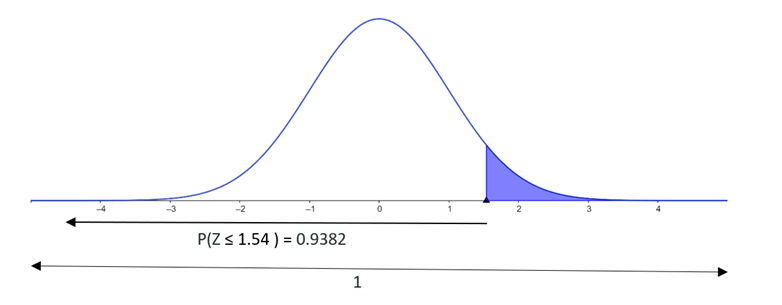
P(-1.54 < Z < 2.35)
Sendo ambos positivos:P(Z ≤ 2.35) - P(Z ≤ -1.54) = 0.9906 - [1 - P(Z < 1.54)] = 0.9906 - 0.0618 = 0.9288
Gráficamente
Zona azul P(-1.54 < Z < 2.35)
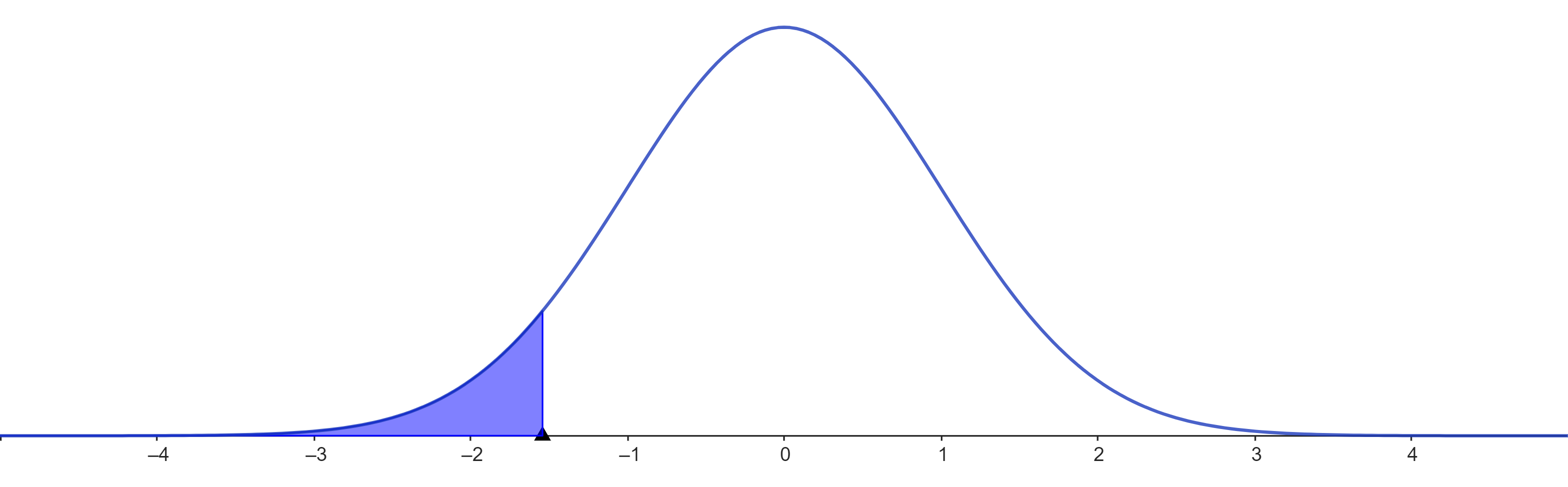
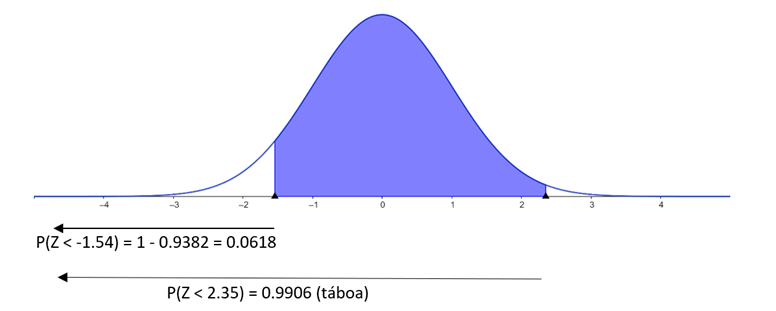
Queda calcular gráficamente P(Z < -1.54), como se fixo no exemplo 3:
Zona azul = P(Z < -1.54)
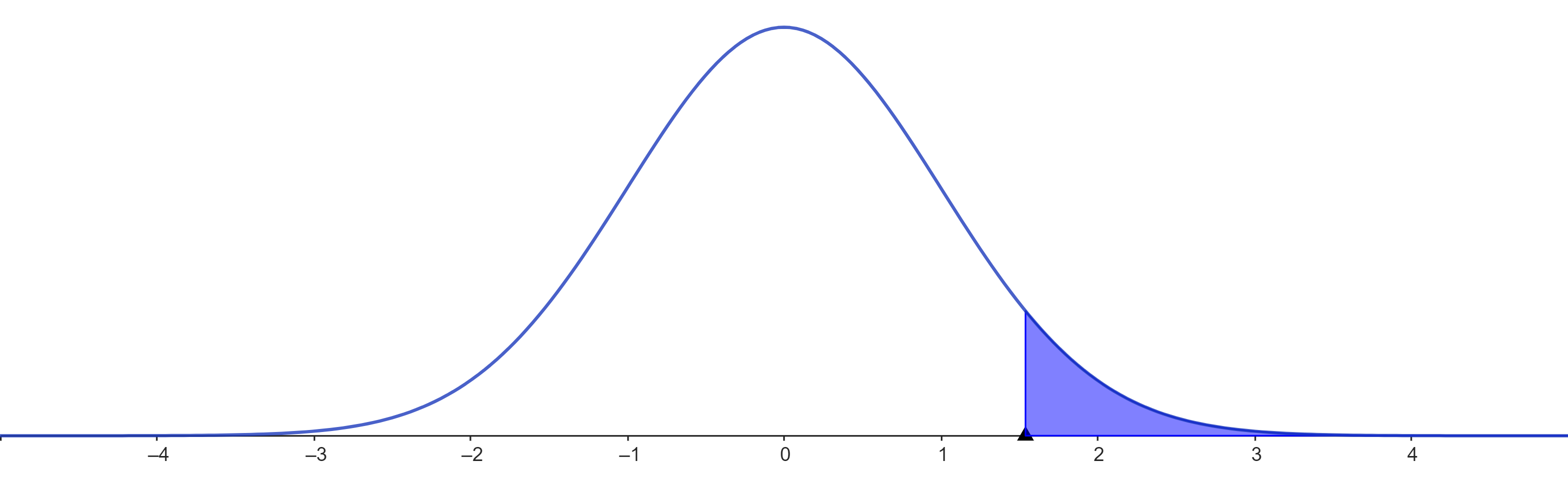
Zona azul = P(Z>1.54)
Polo tanto:
- P(Z = a) = 0. probabilidade de que Z tome un valor exacto "a"
Importante: A probabilidade de que Z tome un valor exacto sempre é 0, xa que a distribución é continua.
Observa que se a é negativo entón -a é un número positivo
Búscase directamente na táboa por ser -a un número positivo