 A distribución normal ten varias características e propiedades craves que a definen.
A distribución normal ten varias características e propiedades craves que a definen.
- En primeiro lugar, a media, a mediana e a moda son iguais entre si.
- Ademais, todos estes valores representan o pico ou punto máis alto da distribución.
- A distribución cae simétricamente ao redor da media, cuxa anchura vén definida pola desviación típica.
A distribución normal módelase con forma de campá e descríbese pola media e a desviación típica, denotándose por \(N(μ, σ)\).
A función de densidade é:
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \]
onde:
- \(x\) = valor da variable ou dos datos examinados e f(x) a función de probabilidade
- \(μ\) = a media
- \(σ\) = a desviación típica (ou desviación estándar)
Propiedades
- \(\int_{-\infty}^{\infty} f(x) dx = 1\)
- En todas as distribucións normais:
- O 68,2% das observacións aparecerán dentro de máis ou menos unha desviación típica da media. Noutras palabras, os valores do intervalo \([\mu-\sigma, \mu+\sigma]\) teñen unha probabilidade de aparecer dun 68,2%.
- O 95,4% das observacións caerán dentro de máis ou menos dúas desviacións típicas. É dicir, os valores do intervalo \([\mu-2\sigma, \mu+2\sigma]\) teñen unha probabilidade de aparecer dun 95,4%.
- O 99,7% dentro de máis ou menos tres desviacións típicas. Doutro xeito,vos valores do intervalo \([\mu-3\sigma, \mu+3\sigma]\) teñen unha probabilidade de aparecer dun 99,7%.
Isto significa que os datos que caen fóra das tres desviacións estándar ("\(\mu\pm 3\sigma\) ") significarían ocorrencias raras.
Gráficamente:
Distribución Normal Estándar
A Distribución Normal Estándar, \(N(0, 1)\), é un caso especial da distribución normal que adopta unha forma específica cunha media e unha desviación estándar dadas:
- Media, μ = 0
- Desviación típica, σ = 1
A súa función de densidade é: \[ f(x) = \frac{1}{ \sqrt{2\pi}} e^{-\frac{x^2}{2}}\]
Distribucións Normal e Normal Estándar
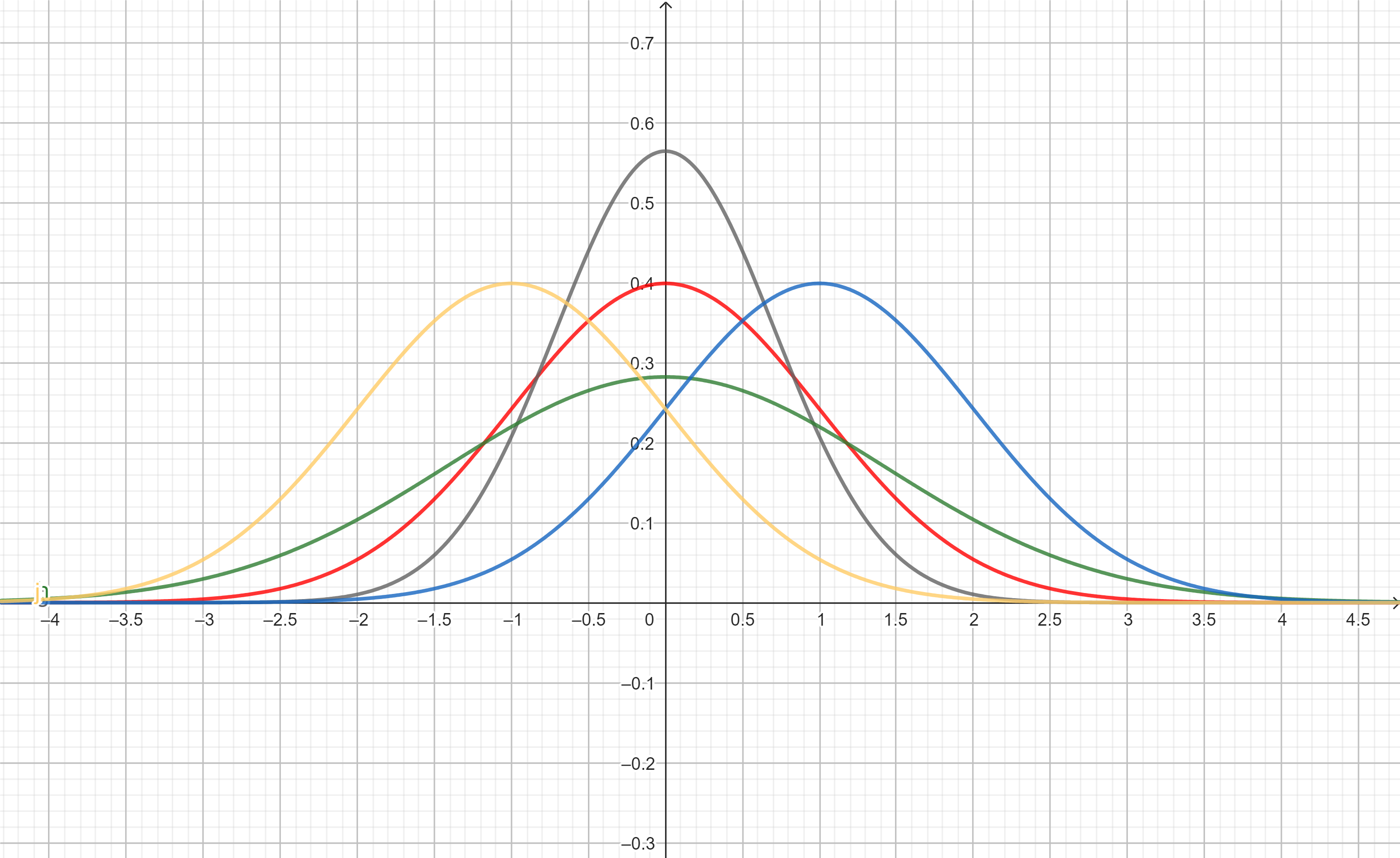
- A función vermella é a distribución normal estándar.
- A verde ten unha desviación típica, σ, menor a 1, polo que se verá "achatada".
- A gris ten unha desviación típica, σ, maior a 1, polo que se verá "estirada".
- A azul ten unha media μ = 1, polo que se desprazará 1 unidade á dereita.
- A laranxa ten unha media μ = -1, polo que se desprazará 1 unidade á esquerda.
Tipificar
A tipificación dunha variable aleatoria normal é un proceso que se utiliza para transformar unha variable aleatoria normal con media \(\mu\) e desviación típica \(\sigma\) nunha variable aleatoria normal estándar con media 0 e desviación típica 1. Este proceso coñécese como estandarización ou normalización.
A tipificación realízase mediante a seguinte transformación:
\[Z = \frac{X - \mu}{\sigma}\]
Onde:
- \(X\) é a variable aleatoria normal orixinal
- \(\mu\) é a media de \(X\)
- \(\sigma\) é a desviación típica de \(X\)
- \(Z\) é a variable aleatoria normal estándar ou tipificada.
- Exemplo
-
Se as alturas nunha poboación seguen unha normal de media 170 cm e desviación 5 cm, cal é a probabilidade de que un individuo mida entre 165 cm e 175 cm?
Trátase dunha \(N(170, 5)\) e pídesenos \(P(165 \le X \le 175)\).
Para poder utilizar a táboa da normal estándar, primeiro teremos que tipificar:
\[P(165 \le X \le 175)=P(\frac{165-170}{5} \le Z \le \frac{175-170}{5})=P({-1} \le Z \le 1)\]
Agora usamos a táboa e calculamos a probabilidade pedida:
\[P({-1} \le Z \le 1) = P(Z \le 1) - P(Z \le {-1}) = 0.8413 - (1-0.8413)= 0.6826 \]
É a suma de todos os datos dividido polo número total de datos
É o dato que ocupa a posición central cando temos os valores ordenados numericamente de menor a maior
É o dato que máis se repite