OPCIÓN A

Os videoxogos que se consumen en Galicia xóganse o 45% en consola e o resto no móbil. Dos que se xogan en consola, o 70% son de acción, o 10% de estratexia e o resto doutras categorías. Dos xogos para móbil, un 25% son de acción, outro 25% de estratexia e o resto doutras categorías.
a) Que porcentaxe dos videoxogos consumidos en Galicia son de acción? b) Elíxese ao azar un xogador que está xogando a un xogo de estratexia cal é a probabilidade de que o estea facendo a través do móbil?

Solución

OPCIÓN B

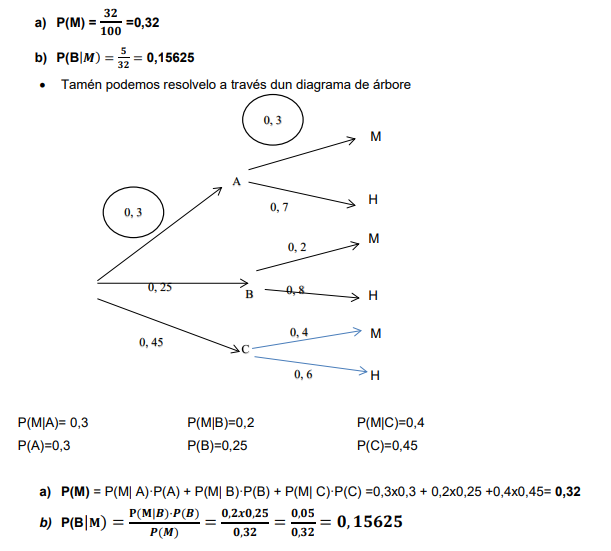
Nunha poboación de cada 100 consumidores de auga mineral, 30 consumen a marca A, 25 a marca B e o resto a marca C. Ademais, o 30% de consumidores de A, o 20% de consumidores de B e o 40% de consumidores de C son mulleres.

a) Selecciónase ao azar un consumidor de auga mineral desa poboación, cal é a probabilidade de que sexa muller? b) Se se seleccionou unha muller ao azar acha a probabilidade de que consuma a marca B

Solución

OPCIÓN A

Nunha cidade, o 20% das persoas que acceden a un centro comercial proceden do centro da cidade, o 45% de barrios periféricos e o resto de pobos próximos. Efectúan algunha compra o 60%, o 75% e o 50% de cada procedencia respectivamente.

a) Se un determinado día visitan o centro comercial 2000 persoas, cal é o número esperado de persoas que non realiza compras? b) Se eliximos unha persoa ao azar que realizou algunha compra nese centro comercial cal é a probabilidade de que proceda dun pobo próximo?

Solución

.

OPCIÓN B

Para a construción dun panel luminoso disponse dun contedor con 200 lámpadas brancas, 150 lámpadas azuis e 250 lámpadas vermellas. A probabilidade de que unha lámpada do contedor non funcione é 0,01 se é branca, 0,02 se é azul e 0,03 se é vermella. Elíxese ao azar unha lámpada do contedor

a) Calcula a probabilidade de que a lámpada non funcione. b) Sabendo que a lámpada elixida funciona, calcula a probabilidade de que dita lámpada non sexa vermella.

OPCIÓN A

Dá resposta aos apartados seguintes:
a) O 40% dos habitantes dunha certa comarca teñen camelias, o 35% teñen rosas e o 21% teñen camelias e rosas. Se se elixe ao azar a un habitante desa comarca, calcular as cinco probabilidades seguintes: de que teña camelias ou rosas; de que non teña nin camelias nin rosas; de que teña camelias, sabendo que ten rosas; de que teña rosas, sabendo que ten camelias; e de que soamente teña rosas ou soamente teña camelias.
b) Se nun auditorio hai 50 persoas, cal é a probabilidade de que polo menos 2 teñan nacido no mes de xaneiro?

Solución

OPCIÓN B

Dá resposta aos apartados seguintes:
a) Sexan 𝐴 e 𝐵 dous sucesos dun mesmo espazo mostral. Calcula 𝑃(𝐴) se 𝑃(𝐵) = 0.8, 𝑃(𝐴 ∩ 𝐵) = 0.2 e 𝑃(𝐴 ∪ 𝐵) é o
triplo de 𝑃(𝐴).
b) Nun determinado lugar, a temperatura máxima durante o mes de xullo segue unha distribución normal de media 25℃
e desviación típica 4℃. Calcula a probabilidade de que a temperatura máxima dun certo día estea comprendida entre
21℃ e 27.2℃. En cantos días do mes se espera que a temperatura máxima permaneza dentro dese rango?

Solución

OPCIÓN A

Dá resposta aos apartados seguintes:
a) A probabilidade de que un mozo recorde regar a súa roseira durante unha certa semana é de 23. Se se rega, a roseira sobrevive con probabilidade 0.7; se non, faino con probabilidade 0.2. Ao finalizar a semana, a roseira sobreviviu. Cal é a probabilidade de que o mozo non a regase?
b) Unha fábrica produce pezas cuxo grosor segue unha distribución normal de media 8 cm e desviación n típica 0.01 cm. Calcula a probabilidade de que unha peza teña un grosor comprendido entre 7.98 e 8.02 cm.

Solución

OPCIÓN B

Dá resposta aos apartados seguintes:
a) Sexan 𝐴 e 𝐵 dous sucesos dun mesmo espazo mostral tales que 𝑃(𝐴) = 0.2, 𝑃(𝐵) = 0.4 e 𝑃(𝐴 ∪ 𝐵) = 0.5. Calcula 𝑃(𝐴̅), 𝑃(𝐵), 𝑃(𝐴∩𝐵) e 𝑃(𝐴̅∪𝐵). Razoa se 𝐴 e 𝐵 son ou non sucesos independentes.
b) A probabilidade de que un determinado xogador de fútbol marque gol desde o punto de penalti é 𝑝 = 0.7. Se lanza 5 penaltis, calcula as seguintes tres probabilidades: de que non marque ningún gol; de que marque polo menos 2 goles; e de que marque 5 goles. Se lanza 2100 penaltis, calcula a probabilidade de que nos 1450 goles. Estase a asumir que os lanzamentos son sucesos independentes.

Solución