OPCIÓN A

Nunha empresa, o 20% dos traballadores son maiores de 30 anos, o 8% desempeña algún posto directivo e o 6% é maior de 30 anos e desempeña algún posto directivo.

a) Que porcentaxe dos traballadores ten máis de 30 anos e non desempeña ningún cargo directivo? b) Que porcentaxe dos traballadores non é directivo nin maior de 30 anos? c) Se a empresa ten 100 traballadores, cantos son directivos e non teñen máis de 30 anos?

Solución

OPCIÓN B

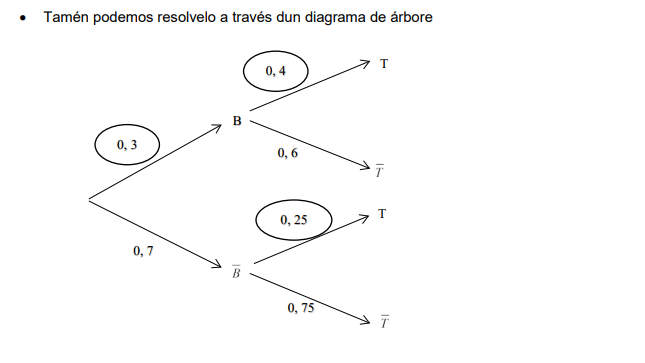
O 30% das estudantes dun instituto practica baloncesto. De entre as que practican baloncesto, o 40% practica ademais tenis. De entre as que non practican baloncesto, un cuarto practica tenis.

Elixida unha estudante dese instituto ao azar, a) Cal é a probabilidade de que practique ambos os deportes? b) Cal é a probabilidade de que practique tenis? c) Son independentes os sucesos “practicar tenis” e “practicar baloncesto”?

Solución

OPCIÓN A

Nunha empresa, o 30% dos empregados son mulleres e o 70% restante son homes. Das mulleres, o 80% teñen contrato indefinido, mentres que do grupo dos homes, só o 70% ten ese tipo de contrato.

a) Calcula a porcentaxe de persoas da devandita empresa que ten contrato indefinido. b) Se un empregado ten contrato indefinido obtén a probabilidade de que sexa muller. c) ¿Son independentes os sucesos “ser home” e “ter contrato indefinido”?

Solución

OPCIÓN B

Nunha poboación de cada 200 consumidores dunha bebida isotónica 60 consumen a marca A, 50 a marca B e o resto a marca C. Ademais, o 30% de consumidores de A, o 20% de consumidores de B e o 40% de consumidores de C son mozos.

a) Selecciónase ao azar un consumidor de dita bebida nesa poboación, cal é a probabilidade de que sexa mozo? b) Se se seleccionou un mozo acha a probabilidade de que consuma a marca B. c) Son independentes os sucesos “ser mozo” e “consumir a marca A”?

Solución

OPCIÓN A

Nas rebaixas duns grandes almacéns están mesturadas eávenda 200 bufandas da marca A, 150 da marca B e 50 da marca C. A probabilidade de que unha bufanda da marca A sexa defectuosa é 0,01; 0,02 seé da marca B e 0,04 se é da marca C. Unha persoa elixe unha bufanda ao azar
a) Calcula a probabilidade de que a bufanda elixida sexa da marca A ou defectuosa.
b) Calcula a probabilidade de que a bufanda elixida non sexa defectuosa nin da marca C.
c) Se a bufanda elixida non é defectuosa, cal é a probabilidade de que sexa da marca B?

Solución

OPCIÓN B

a) Un exame tipo test consta de 10 preguntas, cada unha con 4 respostas das cales só unha é correcta. Se se contesta ao azar, cal é a probabilidade de contestar ben polo menos dúas preguntas?
b) A duración dun certo tipo de pilas eléctricas é unha variable que segue unha distribución normal de media 50 horas e desviación típica 5 horas. Calcula a probabilidade de que unha pila eléctrica deste tipo, elixida ao azar, dure menos de 42 horas.

Solución

OPCIÓN A

Nun bombo temos 10 bolas idénticas numeradas do 0 ao 9 e cada vez que facemos una extracción devolvemos a bola ao bombo
a) Se facemos 5 extraccións, calcula a probabilidade de que o 7 saia menos de dúas veces.
b) Se facemos 100 extraccións, calcula a probabilidade de que o 7 saia menos de nove veces.

Solución

OPCIÓN B

Nunha fábrica hai tres máquinas A, B e C que producen a mesma cantidade de pezas. A máquina A produce un 2% de pezas defectuosas, a B un 4% e a C un 5%.
a) Calcula a probabilidade de que unha peza elixida ao azar sexa defectuosa.
b) Se se elixe unha peza ao azar e resulta que non é defectuosa, cal é a probabilidade de que fora fabricada pola máquina A?

Solución