A función de distribución dunha variable aleatoria discreta \(X\) é unha función que asigna a cada valor \(x\) no rango de \(X\) a probabilidade acumulada de que \(X\) tome un valor menor ou igual a \(x\).
Formalmente, defínese como:
\[F(x) = P(X \leq x) = \sum_{k \leq x} P(X = k)\]
Onde \(P(X = k)\) é a función de masa de probabilidade de \(X\), que asigna a probabilidade de que \(X\) tome cada valor \(k\) no seu rango.
Propiedades
A función de distribución dunha variable discreta ten varias propiedades importantes:
- 0 ≤ F(x) ≤ 1 para todo x
-
F(x) é crecente
-
Límites:
- \(\lim\limits_{x \to -∞}\) F(x) = 0
- \(\lim\limits_{x \to ∞}\) F(x) = 1
-
F(x) é continua pola dereita
-
Propiedades de probabilidade:
- P(a < X ≤ b) = F(b) - F(a)
- P(X > a) = 1 - F(a)
- P(X ≤ a) = F(a)
- Exemplo
-
Consideramos o experimento aleatorio que consiste en lanzar unha moeda e definimos a variable aleatoria que conta o número de cruces.
Espazo mostral: \[Ω=\{\text{0, 1}\}\]
Función de distribución:
\[ F(x) = P(X \leq x) =\begin{cases} 0 & \text{se } x< 0 \\ \frac{1}{2} & \text{se } 0 \leq x<1 \\ 1 & \text{se } x \geq1 \end{cases} \]
Representación da función de distribución: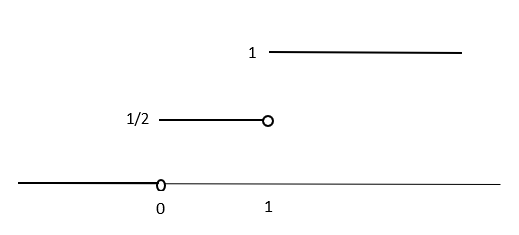
Conxunto dos valores que toma a variable