Diagramas de Árbore
Os diagramas de árbore son unha ferramenta gráfica moi útil na probabilidade para representar todos os posibles resultados dunha serie de experimentos, especialmente cando estes son secuenciais. A través dun diagrama de árbore, pódese visualizar facilmente como os sucesos se ramifican e como as probabilidade se distribúen entre os distintos camiños posibles.
Un diagrama de árbore constrúese comezando coa raíz, que representa o punto inicial antes de que se realice calquera experimento. A partir de aí, as ramas saen da raíz representando todos os posibles resultados do primeiro evento. Cada rama divídese novamente para amosar os posibles resultados do seguinte evento, e así sucesivamente.
As regras principais para traballar con diagramas de árbore son:
-
Multiplicación ao longo das ramas: A probabilidade dun camiño específico no diagrama de árbore obtense multiplicando as probabilidade ao longo das ramas do camiño.
-
Adición entre ramas: A probabilidade dun evento que pode ocorrer en varios camiños diferentes é a suma das probabilidade de todos eses camiños.
Os puntos finais de cada camiño no diagrama de árbore representan os resultados finais do experimento.
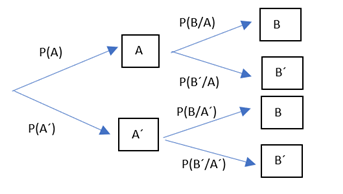
O aspecto dun diagrama de árbore correspondente a un experimento con dúas fases é o seguinte: