Intervalo de confianza para a proporción

Consideramos X unha variable aleatoria B (n, p)

Para tamaños grandes de n, n> 30, a distribución binomial aproxímase a unha distribución normal: 

\(X \to {N(np,} \sqrt{npq}{)}\)

Sabemos de estatística puntual, que a distribución da proporción mostral:

\(\hat p\to N\left ({p,} \sqrt{\dfrac{pq}{n}}\right )\)

Polo tanto, tipificando:

\(Z=\dfrac{\hat p-p}{\sqrt {\dfrac {pq}{n}}}\to N(0, 1)\)

Fixando un nivel de confianza, 1 - α, podemos calcular:

\(P\left(-z<\dfrac{\hat p-p}{\sqrt {\dfrac {pq}{n}}}<z\right)=1-α\)

Operando:

 \(P\left ({\hat p}-z{\sqrt {\dfrac {pq}{n}}}<p<{\hat p}+z{\sqrt {\dfrac {pq}{n}}}\right )=1-\alpha\)

que corresponde ao que queremos:

 \(P\left ({\hat p_1}<p<\hat p_2 \right)=1-α\)

Temos así calculado o intervalo de confianza (p̂₁, p̂₂), onde:

\({\hat p_1}={\hat p}-z{\sqrt {\dfrac {pq}{n}}}\)

\({\hat p_2}={\hat p}+z{\sqrt {\dfrac {pq}{n}}}\)

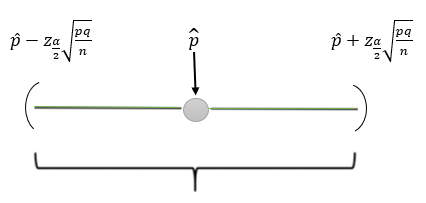
Polo tanto, chamando IC ao intervalo de confianza, queda do seguinte xeito:  \[IC =\left ({\hat p}-z{\sqrt {\dfrac {pq}{n}}}, {\hat p}+z{\sqrt {\dfrac {pq}{n}}}\right )=\left ({\hat p}{\pm}z{\sqrt {\dfrac {pq}{n}}}\right)\]

Para o seu cálculo teremos que atopar o valor z que se chama valor crítico e normalmente se denota por \(z_\dfrac{\alpha}{2}\) xa que o seu valor depende do nivel de significación, α.

Gráficamente:

IMPORTANTE

• Na práctica, o intervalo anterior non é calculable (depende do valor descoñecido p). Para resolver o problema substitúese p polo seu estimador, \( \hat p \). O intervalo resultante é:
   \[IC =\left ({\hat p}-z_\frac {α} {2}{\sqrt {\dfrac {\hat{p} \hat{q}}{n}}}, {\hat p}+z_\frac {α} {2}{\sqrt {\dfrac {\hat{p} \hat{q}}{n}}}\right )=\left ({\hat p}{\pm}z_\frac {α} {2}{\sqrt {\dfrac {\hat{p} \hat{q}}{n}}}\right)\]
• No caso dunha resposta dicotómica onde se descoñece p, só hai que especificar dous parámetros: o nivel de confianza (1 - α) e a semilonxitude do intervalo. Isto débese a que se asume a situación de máxima incerteza, onde p = 0,5. Entón \(p q = \frac 1 4 \) e o intervalo de confianza, na situación de máxima incerteza, é:
   \[IC =\left ({\hat p}-z_\frac {α} {2} {\sqrt {\dfrac {1}{4n}}}, {\hat p}+z_\frac {α} {2}{\sqrt {\dfrac {1}{4n}}}\right )=\left ({\hat p}{\pm}z_\frac {α} {2}{\sqrt {\dfrac {1}{4n}}}\right)\]