Cando a distribución da poboación é normal, a distribución da media mostral tamén é normal.

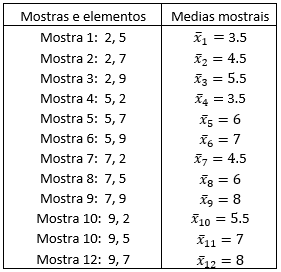
Se dunha poboación se extraen todas as mostras posibles dun determinado tamaño e se calcula a media para cada unha delas, a media destas medias mostrais coincide coa media de toda a poboación.

Para unha distribución normal da poboación con media μ e desviación estándar σ, a distribución da media mostral é normal, con media μ e desviación estándar \(\dfrac {\sigma}{\sqrt{n}}\), é dicir:

\(\overline X\to N\left ({\mu,}\dfrac{\sigma}{\sqrt{n}}\right )\)

Polo tanto, se tipificamos:

\(Z=\dfrac{\overline X-\mu}{\dfrac {\sigma}{\sqrt {n}}}\to N(0, 1)\)

O resultado máis importante sobre as medias mostrais é o Teorema Central do Límite.

Este teorema di que para un tamaño de mostra n suficientemente grande, a distribución da media mostral, aproximarase a unha distribución normal.

Isto é certo para unha mostra de variables aleatorias independentes de calquera distribución poboacional, sempre que a poboación teña unha desviación estándar finita.

Exemplo

As notas de catro estudantes en matemáticas son 2, 5, 7 e 9. A media da poboación é:

Imos extraer todas as mostras de tamaño dous sen repetición, e imos calcular a media de cada unha das mostras:

As medias das mostras (cada unha delas denótase por x̄) non coinciden coa media da poboación, pero si calculamos a media das medias das mostras o resultado é precisamente a media da poboación:

Esta é unha das razóns polas que a media mostral é un bo estimador para a media da poboación.