Na estimación puntual o noso obxectivo era calcular un estimador, \(\widehat{θ} \), tal que \(\theta \) ≈ \(\widehat{θ} \), pero \(\widehat{θ} \) é unha variable aleatoria e raramente coincide co valor do parámetro a estimar.
A alternativa á estimación puntual é construír un intervalo da forma (\(\widehat{θ} \)1, \(\widehat{θ} \)2), tal que:
\(\widehat{θ} \)1 < \(\theta \) < \(\widehat{θ} \)2
cuantificando a probabilidade (nivel de confianza) de que o verdadeiro valor do parámetro estea entre os dous extremos do intervalo:
P( \(\widehat{θ} \)1 < \(\theta \) < \(\widehat{θ} \)2) = 1 - α
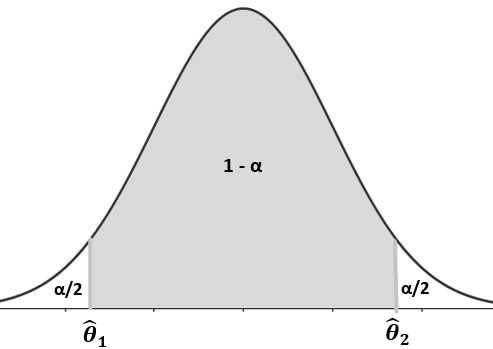
Canto maior sexa o ancho do intervalo, máis probable é que o valor do parámetro caia dentro do intervalo, pero canto maior sexa o ancho do intervalo, menos útil será. Polo tanto, haberá que buscar un equilibrio entre o ancho do intervalo, \(\widehat{θ} \)2 - \(\widehat{θ} \)1, e o nivel de confianza, 1 - α.
1 - α chámase nivel de confianza e α, nivel de significación.
Aproximadamente igual a
Parámetro poboacional que queremos estimar