Elaboración e presentación | Licenza_Mostraxe

Deseño do estudo

Identificar a pregunta.
O primeiro paso do estudo é formular unha pregunta de investigación. Esta é a pregunta á que quere responder o estudo.
Identificar a poboación de interese.
Identificar as variables.
Determinar cales son as variables que se deben medir para responder á pregunta de investigación.
Identificar os tipos de variables (cualitativas, cuantitativas).
Elaborar a enquisa.
Obter unha mostra representativa da poboación (mostraxe).
Determinar as análises estatísticas que se van realizar.

Resumindo, nesta etapa indícase o que se vai medir, como se vai a medir, como se recollerá a mostra, o tamaño da mostra e como se van analizar os datos.

Presentación

Para analizar e interpretar adecuadamente os datos dun estudo é necesario presentalos de maneira ordenada. Para iso:

Elabóranse táboas onde se agrupan os datos
- Táboas de frecuencias
- Táboas de dobre entrada
Represéntanse os datos gráficamente. Os gráficos permiten ver as características dos datos de forma rápida e clara, facer comparacións destes, etc. O tipo de gráfico dependerá do tipo de variable a estudo. En xeral:
- Para variables cualitativas e cuantitativas discretas
- Para variables cuantitativas continuas
  - Histograma
  - Polígono de frecuencias
- Outros tipos de gráficos

Os datos represéntanse mediante barras dunha lonxitude proporcional á frecuencia (absoluta, relativa ou acumulada).

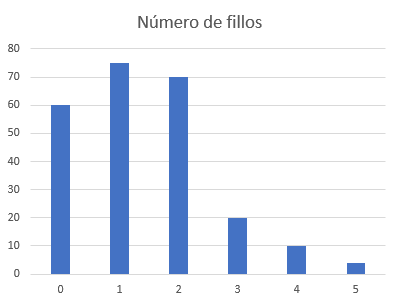
Barras verticais

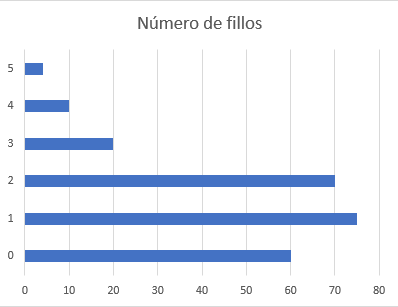
Barras horizontais

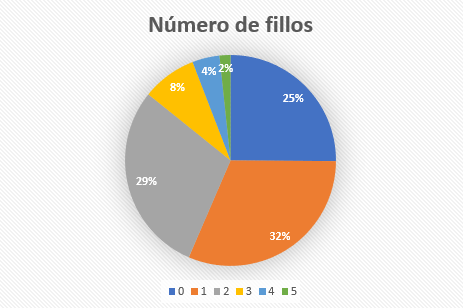
Cada sector representa a porcentaxe dun valor da variable con respecto ao total dos datos, sendo o seu ángulo proporcional á frecuencia correspondente.

A fórmula para calcular o ángulo de cada sector é:

\[α=f_i \frac {360º}{N}\]

sendo f_i a frecuencia de cada dato e N o número total de datos.

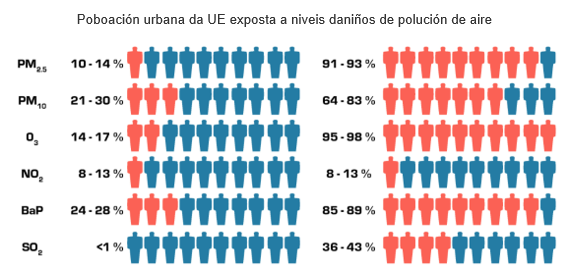
Representa mediante debuxos a característica estudada. Cantos máis debuxos en cada categoría ou canto maior sexa o debuxo, maior será a frecuencia.

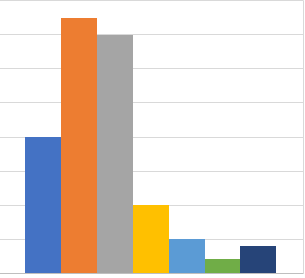
É semellante a un gráfico de barras, pero un histograma agrupa os resultados en intervalos. A altura de cada barra indica cantos resultados caen en cada intervalo.

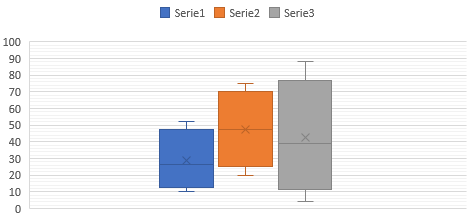
Mostra o resumo de cinco números dun conxunto de datos: o mínimo, o primeiro cuartil, a mediana (segundo cuartil), o terceiro cuartil e o máximo.

Constrúese organizando os valores de datos recollidos en orde ascendente de magnitude coas súas correspondentes frecuencias.

x_i	f_i	F_i	h_i	H_i	%
0	53	53	0.42	0.42	42.06
1	47	100	0.37	0.79	37.30
2	26	126	0.21	1	20.63
	126		1		100

x_i: os distintos datos recollidos
f_i: frecuencia absoluta de cada dato
F_i: frecuencia absoluta acumulada
h_i: frecuencia relativa
H_i: frecuencia relativa acumulada
%: porcentaxe

Formada polas frecuencias absolutas de todos os posibles pares de valores da variable estatística bidimensional (X, Y)

	x₁= 2	x₂= 4	x₃= 7	Totais
y₁=3	f₁₁= 3	f₂₁ = 2	f₃₁ = 1	6
y₂=5	f₁₂ = 1	f₂₂ = 4	f₃₂ = 2	7
Totais	4	6	3	13

f_ij = frecuencia absoluta do par (x_i, y_j)

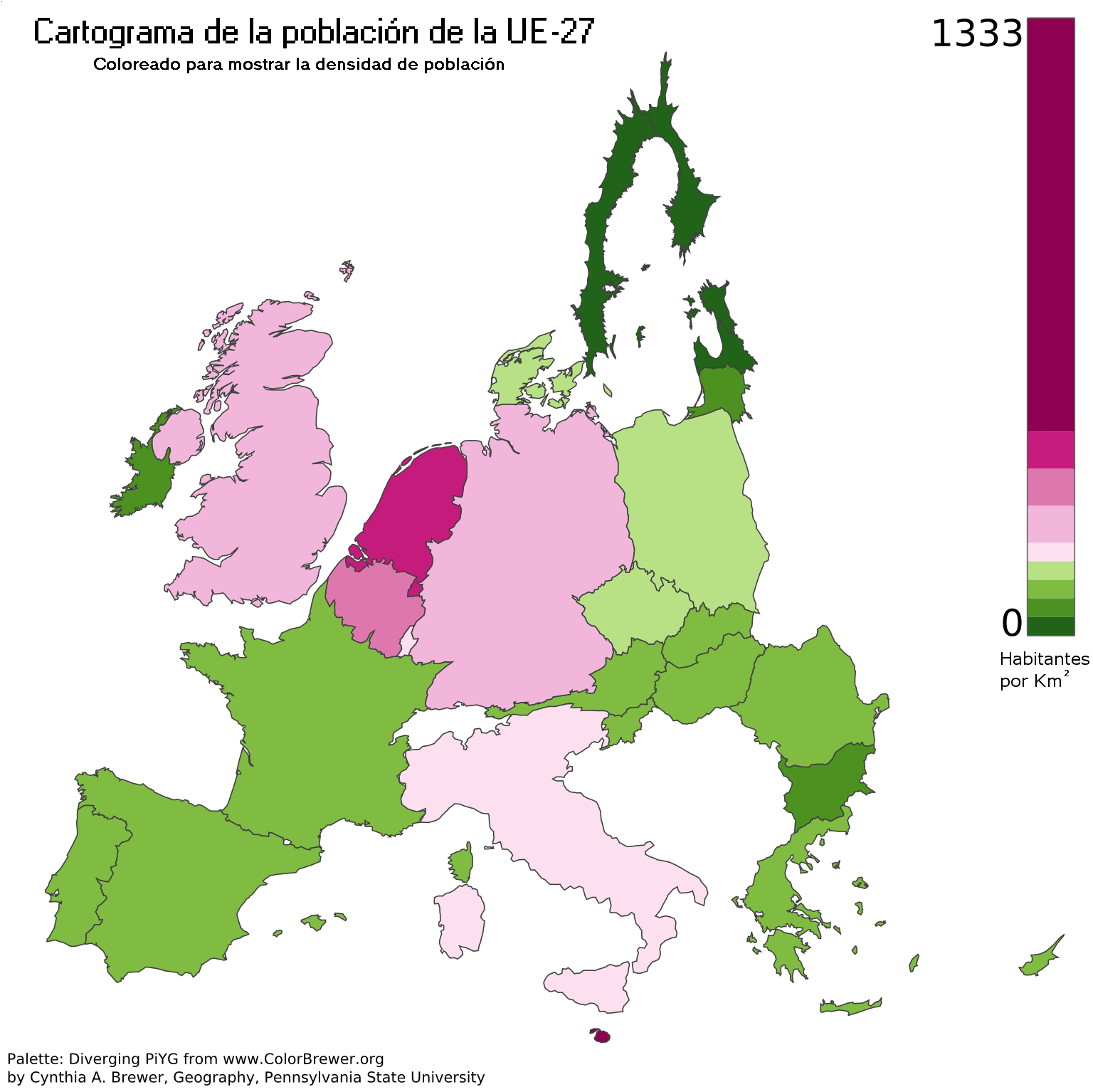
É un gráfico tipo mapa no que se presentan os datos estatísticos.

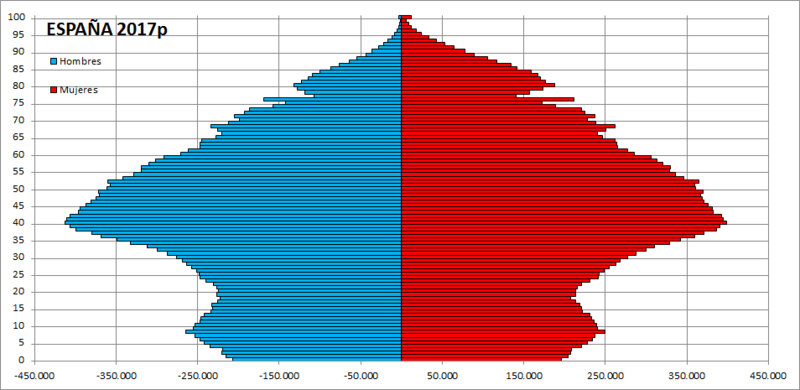
É un gráfico de barras horizontais que serve para coñecer a porcentaxe da poboación por sexo e por idade.

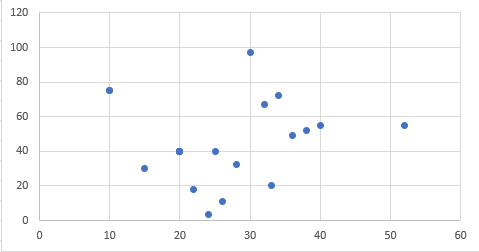
Utilízase en estudos de dúas variables (bidimensionais). No diagrama represéntanse os pares de valores recollidos no estudo (X, Y), para analizar se existe algún tipo de relación entre as dúas variables.

Únense mediante unha liña os puntos medios das columnas do histograma.