O erro de estimación depende do tipo de intervalo de confianza que imos utilizar.
Erro na proporción mostral
Tendo en conta que:
\[IC =\left ({\hat p}-z_\frac {α} {2}{\sqrt {\dfrac {\hat{p} \hat{q}}{n}}}, {\hat p}+z_\frac {α} {2}{\sqrt {\dfrac {\hat{p} \hat{q}}{n}}}\right )=\left ({\hat p}{\pm}z_\frac {α} {2}{\sqrt {\dfrac {\hat{p} \hat{q}}{n}}}\right)\]
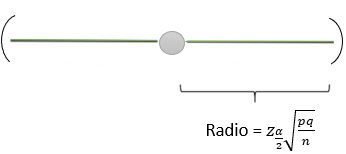
Como o intervalo é simétrico, o erro (E) é o radio do intervalo, é dicir:
\[E =z_\frac {α} {2}{\sqrt {\dfrac {\hat{p} \hat{q}}{n}}}\]
Importante:
- Recorda que zα/2 chámase valor crítico e hai que atopalo na táboa da distribución N(0, 1).
- O erro no caso da proporción ven expresado en tanto por un.
Erro na media mostral
Tendo en conta que:
\[IC =\left ({\overline x}-z\dfrac{\sigma}{\sqrt{n}}, {\overline x}+z\dfrac{\sigma}{\sqrt{n}}\right )=\left ({\overline x}{\pm}z\dfrac{\sigma}{\sqrt{n}}\right)\]
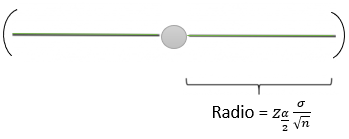
Como o intervalo é simétrico, o erro (E) é o radio do intervalo, é dicir:
\[E=z\dfrac{\sigma}{\sqrt{n}}\]
Importante:
- Recorda que zα/2 chámase valor crítico e hai que atopalo na táboa da distribución N(0, 1).
É a distancia dende o estatístico utilizado ata cada extremo do intervalo de confianza. Se o intervalo é simétrico, a marxe de erro é a metade do ancho do intervalo de confianza, ou noutras palabras, é o raio do intervalo.
α/2 é a cola da campana de Gauss cando o nivel de significación é α
α/2 é a cola da campana de Gauss cando o nivel de significación é α