Intervalo de confianza para a media | Licenza_Mostraxe

Consideramos X unha distribución que segue unha normal de parámetros μ e σ, con σ coñecida, pero μ descoñecida.

\(X\to N\left ({\mu,}\hspace{0,25cm}{ \sigma}\right)\)

Consideramos unha mostra de tamaño n e calculamos a media mostral X̄.

Sabemos de estatística puntual, que a distribución da media mostral:

\(\bar{X}\to N\left ({\mu,}\dfrac{\sigma}{\sqrt{n}}\right )\)

Polo tanto, tipificando:

\(Z=\dfrac{\bar{x}-\mu}{\dfrac {\sigma}{\sqrt {n}}}\to N(0, 1)\)

Fixando un nivel de confianza, 1 - α, podemos calcular:

\(P\left(-z<\dfrac{\bar{x}-\mu}{\dfrac {\sigma}{\sqrt {n}}}<z\right)=1-α\)

Operando:

\(P\left ({\bar{x}}-z\dfrac{\sigma}{\sqrt{n}}<\mu<{\bar{x}}+z\dfrac{\sigma}{\sqrt{n}}\right )=1-\alpha\)

que corresponde ao que queremos:

\(P\left(\bar{x}_1<μ<\bar{x}_2\right)=1-α\)

Queda así calculado o intervalo de confianza (x̄₁, x̄₂), onde:

\({\bar{x}_1}={\bar{x}}-z\dfrac{\sigma}{\sqrt{n}}\)

\({\bar{x}_2}={\bar{x}}+z\dfrac{\sigma}{\sqrt{n}}\)

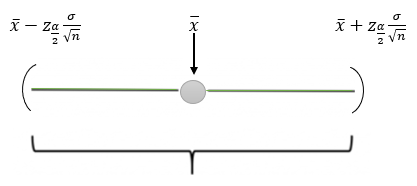
Polo tanto, chamando IC ao intervalo de confianza, temos: \[IC =\left ({\bar{x}}-z\dfrac{\sigma}{\sqrt{n}}, {\bar{x}}+z\dfrac{\sigma}{\sqrt{n}}\right )=\left ({\bar{x}}{\pm}z\dfrac{\sigma}{\sqrt{n}}\right)\]

Para o seu cálculo teremos que atopar o valor z, que se chama valor crítico e normalmente se denota por \(z_\dfrac{\alpha}{2}\) xa que o seu valor depende do nivel de significación, α.

Gráficamente:

Exemplo

O peso das vacas leiteiras dunha granxa distribúese normalmente, con desviación típica de 5 quilogramos. Tómase ao azar unha mostra de 16 delas para o seu transporte. Sabendo que o peso medio resulta ser de 503.75 quilogramos, determinar un intervalo de confianza para o peso medio das vacas cun nivel de significación do 8%.

Do enunciado obtemos que:

n = 16
σ = 5
\(\bar{x}\) =503.75
α = 0.08 \(\Rightarrow\) \(\frac {α} {2}\) = 0.04

Sabemos que \[IC =\left ({\bar{x}}-z_\frac {α} {2}\dfrac{\sigma}{\sqrt{n}}, {\bar{x}}+z_\frac {α} {2}\dfrac{\sigma}{\sqrt{n}}\right )\]

Polo tanto, cos datos do enunciado:

\[IC =\left (503.75-z_\frac {α} {2}\dfrac{5}{\sqrt{16}}, 503.75+z_\frac {α} {2}\dfrac{5}{\sqrt{16}}\right )\]

Agora só nos queda calcular o valor crítico, \(z_\frac {α} {2}\), nas táboas da N(0, 1):

Como \(z_\frac {α} {2}\) = 1.40, teremos:
\[IC =\left (503.75-1.40\dfrac{5}{\sqrt{16}}, 503.75+1.40\dfrac{5}{\sqrt{16}}\right )= (547.75, 531.71)\]

Temos unha confianza do 92% de que o peso medio das vacas estea entre 547.75 e 531.71 quilogramos.

Ampliación

Cando se descoñece o valor de σ ou se quere estimar a varianza, débense utilizar distribucións distintas á normal, como a t de Student ou a Ji-cadrado (χ₂). Nas seguintes páxinas pódese ver, non só o manexo das súas táboas, senón tamén o seu uso para o cálculo de intervalos de confianza.

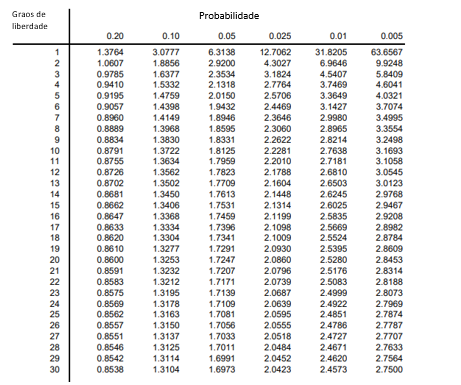
Táboa t-Student

Contén os valores de a tales que \(P(t_{n-1}\geq a)=p\), onde n-1 son os Graos de Libertade, con n o tamaño da mostra.

Intervalo de confianza para a media da poboación con σ descoñecida

Neste caso utilizamos como estimador da varianza a cuasivarianza, \(s^2_{n-1}\). Entón se temos un nivel de confianza de 1- α, o intervalo de confianza para a media poboacional é:

\[IC=\left(\overline{x}-t_{\frac{α}{2}, (n-1)}\cdot \frac{s_{n-1}}{\sqrt{n}}, \overline{x}+t_{\frac{α}{2}, (n-1)}\cdot\frac{s_{n-1}}{\sqrt{n}}\right)=\left(\overline{x}\pm t_{\frac{α}{2}, (n-1)}\cdot\frac{s_{n-1}}{\sqrt{n}}\right)\]

EXEMPLO:

Sábese que as vendas semanais dun determinado produto en supermercados segue unha distribución normal. Para estimar o número medio de vendas semanais, recóllese unha mostra de 9 supermercados, obtendo unha media de 16.2 e unha cuasivarianza igual a 22.9. Determine un intervalo ao 95% de confianza para o número medio das devanditas vendas.

Os datos do problema son:

X = número de vendas dun determinado produto en supermercados \(\to N\left ({\mu,}\hspace{0,25cm}{ \sigma}\right)\)
n = 9
\(\overline x\) = 16.2
\(s^2_{n-1}\) = 22.9 \(\Rightarrow\) \(s_{n-1}=\sqrt{22.9}= 4.785\)
1 - α = 0.95 \(\Rightarrow\) \(\frac {α} {2}\) = 0.0025 \(\Rightarrow\) t_{0.025, 8} = 2.3060

Substituíndo:

\[IC=\left(16.2-2.3060\frac{4.785}{\sqrt{9}}, 16.2+2.3060\frac{4.785}{\sqrt{9}}\right)=(12.5, 19.9)\]

Temos unha confianza do 95% de que o número medio de vendas estea entre 12.5 e 19.9.

Táboa Ji-cadrado, χ²

A táboa da distribución Ji-cadrado (tamén chamada Chi-cadrado), contén os valores de a tales que \(P(χ_{n-1}\geq a)=p\), onde n-1 son os Graos de Libertade, con n o tamaño da mostra.

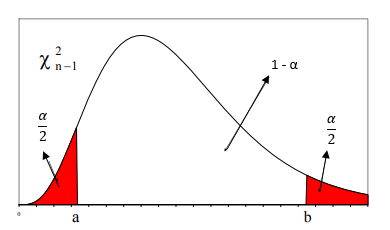
Intervalo de confianza para a varianza

Se o nivel de confianza é 1- α, s²a cuasivarianza e n o tamaño mostral, o intervalo de confianza para a varianza poboacional virá dado por:

\[IC=\left(\frac{(n-1)s^2_{n-1}}{b},\frac{(n-1)s^2_{n-1}}{a}\right)\]

onde a e b son os seguintes valores da distribución \(χ^2_{n-1}\), que hai que buscar na táboa:

EXEMPLO:

O número de visitantes á Torre de Hércules durante o mes de xullo segue unha distribución normal con parámetros descoñecidos. Obtívose unha mostra aleatoria de 10 días en xullo, na que a cuasidesviación tipica é igual a 60,07.

Calcula un intervalo de confianza para a varianza da poboación cun nivel de confianza do 90%.
Calcula un intervalo de confianza para a desviación típica da poboación co nivel de confianza anterior.