7.1 Solucións das actividades complementarias

S19.             

A temperatura da auga é maior ás 12 horas, xa que se moven con maior velocidade.

S20.         

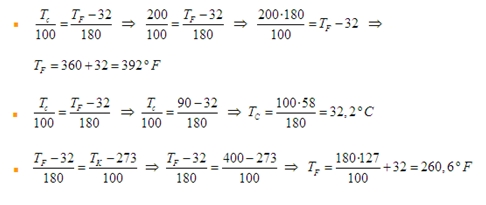
S21.             

• Na primeira frase está mal utilizado. Cando a temperatura é elevada, o noso cerebro interprétao así, e vulgarmente dicimos que temos calor. Falando correctamente deberiamos dicir que notamos unha temperatura demasiado alta.
• A segunda frase tamén é incorrecta. As mantas, e a roupa en xeral, nin dá calor nin o quita. As mantas dificultan que o noso corpo lle ceda calor ao aire.
• A terceira frase é correcta: se un edificio está mal illado, a calor pode pasar do seu interior (quente) ao exterior (frío).       

S22.             

O metal é bo condutor da calor, polo que grande cantidade de calor pasa con facilidade da nosa man ao ferro; o noso cerebro interpreta esta perda de calor como “frío”. Iso non ocorre cos illantes térmicos como a madeira.

S23.             

Porque o aire que rodea o radiador quece e sobe cara ao teito. Se o radiador estivese preto do teito o aire quente quedaría alí arriba e o aire frío abaixo e non se formarían correntes de convección: o aire quente quedaría arriba e o frío abaixo.

S24.             

As reixas serven para evacuar os gases tóxicos ou molestos da cociña. Pola reixa inferior escapan os gases máis densos que o aire, como o butano sen queimar ou o dióxido de carbono. Pola reixa superior escapan os gases menos densos que o aire (como o gas natural, metano) e os que están quentes, como o vapor de auga e os fumes.

S25.             

Para que o termómetro chegue a estar en equilibrio térmico co noso corpo e estea a igual temperatura que el.

S26.             

Porque se o líquido ocupa todo o recipiente e dilata, rebentará o recipiente, aínda que sexa metálico.

S27.             

Se o líquido ten auga e conxela, a auga aumenta de volume e rebentará o frasco

S28.             

A calor só existe entanto que estea a pasar dun corpo a outro. Tránsito significa desprazamento dun sitio a outro

S29.             

A auga líquida está a maior temperatura que o xeo; daquela pasa calor do líquido ao xeo chegando este a fundir.

S30.         

A calor é unha forma da enerxía que pasa duns corpos a outros cando están a diferente temperatura. A calor pode propagarse de tres xeitos distintos: por condución, por convección e por radiación. Os corpos que conducen ben a calor chámanse condutores, e os que a conducen mal, illantes.

S31.         

Porque uns conducen a calor mellor e outros peor; canto menos condutores da calor máis abrigo dan.

S32.         

A temperatura final ten que ser maior que 10 ºC e menor que 60 ºC; ademais, o vaso de 60 ºC ten máis líquido, daquela a temperatura final estará máis próxima a 60 ºC que a 10 ºC. Por tanto, a resposta correcta é 45 ºC.

S33.         

Énchese o oco entre as dúas paredes cun illante térmico para diminuír o paso de calor por condución entre o interior e o exterior da vivenda.

S34.         

• a) Falsa, a temperatura mide a velocidade media do movemento caótico das moléculas.
• b) Falsa, están en equilibrio térmico cando teñen todos igual temperatura.
• c) Verdadeira.

    

S36.             

Non; se o fixese morreriamos. As reaccións químicas que ocorren no noso organismo liberan a calor suficiente para mantérmonos a unha temperatura bastante máis elevada que a do noso contorno, xeralmente.

S37.             

Cando o vapor de auga das nubes condensa a líquido antes de chover, a auga desprende calor que aumenta a temperatura do aire.

S38.             

A densidade é , así que cando dilata o volume aumenta, daquela na fracción  aumenta o denominador e a fracción (densidade), diminúe de valor.

S39.             

Os vasos termo teñen dúas paredes, normalmente de vidro (illante térmico que dificulta a condución da calor), unha interior e outra exterior. Entre elas hai outro illante ou, mellor, faise o baleiro, para impedir a transmisión de calor por condución e por convección. Por último, as paredes de vidro son espellos, para que a calor emitida por radiación reflicta neles e volva ao interior do termo. O vaso termo impide o paso de calor tanto do interior ao exterior por ao revés, daquela tamén serve para conservar frío un líquido.

S40.             

Non, co aumento da temperatura dilata e medirá máis de un metro de longo.

S41.             

Non. Os termómetros clínicos poden medir ata 42 ºC aproximadamente. A auga ferve a 100ºC; daquela, se vostede introduce un termómetro clínico de mercurio en auga demasiado quente, o termómetro rachará, e o mercurio espallarase, o cal é perigoso, xa que o mercurio é moi tóxico.

S42.             

Temperatura ºC	Temperatura ºF	Temperatura K
50	122	323
-100	- 148	173
727	1340,6	1000
0	32	273
-17,8	0	255,2
-273	-459,4	0

S43.             

Si, xa que usamos as mans para tocar, e deste xeito o noso organismo decátase rapidamente se un corpo está demasiado frío ou quente para nós.

S44.             

Un aumento de temperatura de 1 ºC equivale a un aumento de 1 K. Por exemplo, se un corpo está a 20 ºC e aumenta a 21 ºC, na escala Kelvin a súa temperatura pasa de 293 K a 294 K, así que tamén sobe un grao.

A razón disto é que nas escalas celsius e kelvin o intervalo que vai da temperatura de fusión ao de ebulición da auga divídese nas dúas en 100 graos. Non ocorre o mesmo coa escala fahrenheit, na que ese intervalo está dividido en 180 graos; daquela un aumento de 1 ºC equivale a un aumento de 1,8 ºF.

S45.         

Póndoo nunha mestura de auga e xeo: así marcamos no termómetro o 0 ºC. Logo metémolo en auga destilada fervendo para debuxar a marca de 100 ºC. Por último, dividimos o intervalo entre as dúas marcas en cen partes iguais.

S46.         

Só pode estar nas escalas celsius e fahrenheit, xa que na kelvin non hai temperaturas negativas.

 

S50.             

Monomio	- 6x4	4x4y3z	-5x3y2	3x	6
Coeficiente	-6	4	-5	3	6
Grao	4	8	5	1	0

 

S51.             

• 2x + x = 3x
• 3x-5x = -2x
• x² + 3x² +4x² – 5x^{2 =} 3x²
• x²y+3yx^{2 =} 4x²y

S52.             

• 8x-5x = 3x
• 5a² -2a² = 3a²
• 8x³-2x³-4x³ = 2x³
• 5a²-9a² = -4a²

S53.             

• 6x +4 +2x – 9 = 6x+2x+4-9 = 8x-5
• 4a + 3a² -5a + 2a² = 3a²+2a²+4a-5a = 5a²-a
• 4x²+5-x²+2x-8 = 4x²-x²+2x-8+5 = 3x²+2x-3
• 20-6x+2x²-14-8x = 2x²-6x-8x+20-14 = 2x²-14x+6

S54.             

• (10x + 4) - (4x -6) = 10x + 4 - 4x +6 = 10x - 4x +6+ 4 = 6x + 10
• (6x² -8 ) – ( 2x² -3x + 12 ) = 6x² -8 – 2x² +3x - 12 = 6x²– 2x² +3x -12-8 = 4x²+3x-20
• (7x²-x +3) – (2x²-4x +7 ) = 7x²-x +3 – 2x²+4x -7 = 7x²– 2x²+4x -x +3 -7 = 5x²+3x-4
• (3x² +x -6 ) – (8 -2x² -2x ) = 3x² +x -6 – 8 +2x² +2x = 3x² +2x² +2x+x-6 -8 = 5x²+3x-14

S57.             

O grao de un polinomio é o maior dos graos dos monomios que forman o polinomio.Polo tanto:

• x²+3x-5x³+9      Grao 3
• x⁴-9 +3x                        Grao 4
• 6x³-3x²              Grao 3
• 3x-8                   Grao 1

S58.             

• P(x) = x⁴+x²-3x²-2x+6  para x = 2

P(2) = 2⁴+2²-3·2²-2·2+6 = 16+2 – 12 -4 +6 = 8

• P(x) = x⁴ – 9x² + 5        para x = - 3

P(-3) = (-3)⁴ – 9(-3² )+ 5 = 81-81+5 = 5

S59.             

P(x)+Q(x) = (3x³-5x²-4x+4 ) + ( 2x³-x²-7x-1) = 3x³-5x²-4x+4 + 2x³-x²-7x-1 = 3x³+ 2x³-5x²-x²

- 4x-7x+4-1 = 5x³-6x² -11x+3

S60.             

P(x)-Q(x) = (3x³-5x²-4x+4)-(2x³-x²-7x-1) = (sacamos as parénteses lembrando que se hai un signo menos diante de paréntese ao sacalo temos que cambiar os signos, onde hai máis pomos menos e onde hai menos pomos máis)

 = (3x³-5x²-4x+4) - (2x³-x²-7x-1) = 3x³-5x²-4x+4-2x³+x²+7x+1 = 3x³-2x³-5x²+x²-4x+7x+4 +1 = x³-4x²+3x+5

S61.             

• 3·(2x-5) = 3.2x-3·5 = 6x-15
• 8 · (x³-2) = 8·x³-16                              
• x²·(4x-3) = x²·4x -3x² = 4x³-3x²
• 3x · (2x²-3x+2) = 3x·2x²-3x·3x+3x·2 = 6x³-9x²+6x               
• (-2)·(5x-3) = -2·5x-2·(-3) = -10x+6                             
• 3x²·(x-2) = 3x²·x-3x²·2 = 3x³-6x²

S62.             

• ( x+4)² = (x)² + 2·(x)·(4) + (4)^{2 =} x²+8x+16
• (a-1)² = (a)² – (2)·(a)·(1) +(1)² = a² – 2a +1
• (x +6) · (x-6) = (x)²-(6)² = x²-36

S63.             

• 8x + 8y = 8 (x+y)
• x²+xy = x·(x+y)
• 3a +3b = 3·(a+b)
• 2a²+6a = 2a·(a+3)

S65.             

• 2
• 1
• 2
• 5
• 6
• 6

S66.             

• (x – 1) – (x – 5) = x – 1 – x + 5 = 4
• 2x + (1 + x) = 2x + 1 + x = 3x + 1

• 5x – (3x – 2) = 5x – 3x + 2 = 2x + 2
• (3x – 4) + (3x + 4) = 3x – 4 + 3x + 4 = 6x
• (1 – x) – (1 – 2x) = 1 – x – 1 + 2x = x
• (2 – 5x) – (3 – 7x) = 2 – 5x – 3 + 7x = 2x – 1

S67.             

• 2x² – 2x + 8
• x + 2
• 3x² – 8x + 2
• x² + 2x – 18

S68.             

• (2x² – 5x + 6) – 2(x² – 3x + 3) = 2x² – 5x + 6 – 2x² + 6x – 6 = x
• 2 (5x² – 4x + 2) – (8x² – 7x + 4) = 10x² – 8x + 4 – 8x² + 7x – 4 = 2x² – x
• 3 (x – 2) – 2 (x – 1) – (x + 1) = 3x – 6 – 2x + 2 – x – 1 = –5
• 2 (x² – 1) + 4 (2x – 1) – 11x = 2x² – 2 + 8x – 4 – 11x = 2x² – 3x – 6

S69.             

• A + B = x3 + 3x2 – 3x + 10
• A – B = x3 – 3x2 – 7x – 2
• A – C = –x + 12
• B + C = x3 + 3x2 – 2x – 2
• A + B + C = 2x3 + 3x2 – 7x + 2
• A – B – C = –3x2 – 3x + 6

S70.             

• 3x · (x³ – 2x + 5) = 3x⁴ – 6x² + 15x
• (x + 2) · (x – 5) = x² – 5x + 2x – 10 = x² – 3x – 10
• (x² – 2) · (x² + 2x – 3) = x⁴ + 2x³ – 3x² – 2x² – 4x + 6 = x⁴ + 2x³ – 5x² – 4x + 6
• (x³ – 5x² + 1) · (x² – 3x + 1) = x⁵ – 3x⁴ + x³ – 5x⁴ + 15x³ – 5x² + x² – 3x + 1 =

 = x⁵ – 8x⁴ + 16x³ – 4x² – 3x + 1

S71.             

• x² + 12x + 36
• 64 + 16a + a2
• 9 – 6x + x²
• (ba)² – 6ba + 9

• x² – 16
• y ² – a²
• 4x² – 12x + 9
• 9a² – 30ab + 25b²

S72.             

• 5 (a + b – c)
• a (3 – 4b + 2c )
• x (x + 2)
• 2 (x – 2y)
• 3 (x + 2y + 3)
• 3x² (2 – 1 + 3x)

S73.             

• x² + 2xy + y^{2 =} (x + y)²
• 4a²b⁴ – 4ab² + 1 = (2ab² – 1)²
• 4x² – 4x + 1 = (2x – 1)²
• 3x³ – 3x = 3x (x² – 1) = 3x· (x + 1)· (x – 1)
• 6x² – 9x³ = 3x²·(2 – 3x)
• 5x² + 10x + 5 = 5· (x + 1)²
• 4x² – 25 = (2x + 5)· (2x – 5)
• 16x⁶ – 64x⁵ + 64x⁴ = 16x⁴ (x² – 4x + 4) = 16x⁴ ·(x – 2)²