3.1.4 Polinomios
- Polinomio é a suma ou resta de varios monomios. Cada un dos monomios é un termo, e se hai un termo que non teña parte literal (letras) é o termo independente.
- Grao dun polinomio é o grao do monomio de maior grao.
- Coeficientes dun polinomio son os coeficientes dos monomios que o forman.
- Termo independente dun polinomio é o monomio que non ten parte literal (letras).
Exemplo: sexa o polinomio x5-4x3+5x2+8x-9
|
Termos |
Grao |
Coeficientes |
Termo independente |
|
x5, -4x3 ,5x2 ,8x, -9 |
5 |
1 , -4 , 5 , 8 , -9 |
-9 |
Valor numérico dun polinomio
O valor numérico dun polinomio é o valor que se obtén ao substituír a variable por un número e efectuar as operacións.
Exemplo: calcular o valor numérico do polinomio x5-4x3+5x2+8x-9 para un valor de x = 2. O que facemos é substituír no polinomio a variable x polo valor 2.
25-4·23+5·22+8·2-9 = 32-4·8+5·4+8·2-9 = 32-32+20+16-9 = 27
Operacións con polinomios
- Sumar polinomios: para sumar polinomios temos que seguir este procedemento:
– Colócanse os polinomios, ordenados un debaixo do outro, de xeito que coincidan os monomios semellantes.
– Súmanse os coeficientes dos monomios semellantes e ponse a mesma parte literal.
Exemplo:
sumar os polinomios P(x) = 10x5-18x3+14x2+16; Q(x) = -6x4+8x3-6x2+12x-4
Colocamos os polinomios: 10x5 -18x3 +14x2 +16
-6x4 +8x3 -6x2 +12x -4
10x5-6x4-10x3+ 8x2+ 12x-10
- Restar polinomios: para restar polinomios o que se fai é sumar ao primeiro o oposto do segundo.
Exemplo: dados P(x) = 10x5-18x3+14x2+16 ; Q(x) = -6x4+8x3-6x2+12x-4.
Calcular P(x)-Q(x)
10x5 -18-6x4 +14x2 +16
+6x4 - 8x3 + 6x2 -12x +4
10x5 +6x4 - 26 x3 +20 x2-12x +20
- Multiplicar polinomios: o procedemento para multiplicar dous polinomios é o seguinte:
– Colócanse os polinomios, ordenados un debaixo do outro, de xeito que coincidan os monomios semellantes. Se falta algún grao, déixase un oco para que nos sexa máis doado colocar os produtos parciais.
– Para multiplicar polinomios comézase pola esquerda e multiplícase o primeiro monomio do segundo polinomio por todos os monomios do primeiro polinomio; os coeficientes multiplícanse e os expoñentes súmanse. Se falta o termo dalgún grao déixase un oco.
– Continúase multiplicando os demais monomios do segundo polinomio.
– Súmanse todos os polinomios obtidos.
Exemplo: multiplicar os polinomios P(x) · Q(x)
P(x) = 4x3-6x2 +5 Q(x) = 2x2-8x+6
Débese comezar a multiplicar pola esquerda. Primeiro multiplícanse os signos, a continuación os coeficientes e por último súmanse os expoñentes.
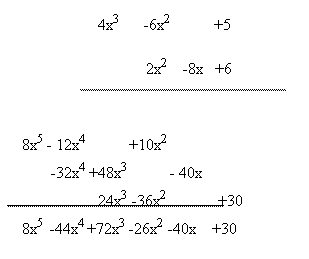
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0