3.1.3 Monomio
Un monomio é o produto indicado dun valor coñecido, representado por un número (coeficiente) por un ou varios valores descoñecidos, representado por letras (parte literal). A parte literal pode ter expoñentes naturais.
Exemplos:

Grao dun monomio
O grao dun monomio é o expoñente da variable que forma a parte literal. Se ten máis dunha variable súmanse os expoñentes.
Exemplos:
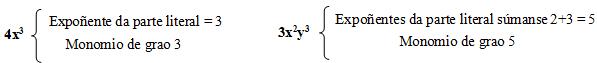
Monomios semellantes
Chamamos monomios semellantes a aqueles que teñen a mesma parte literal.
Exemplos:
2x ; -3x ; x. Son monomios semellantes, xa que a parte literal é idéntica.
3 x2 y3 ; x2 y3. Son monomios semellantes, xa que a parte literal é idéntica.
Valor numérico dun monomio
O valor numérico dun monomio é o valor que se obtén ao substituír a variable ou as variables por un número e efectuar as operacións.
Exemplo: o valor numérico do monomio 3x2y para os valores de x = 2 e y = 3 será:
3x2y ð 3·22·3 = 3·4·3 = 36
Operacións con monomios
- Suma e resta de monomios. Podemos atopar dous casos: se os monomios son semellantes ou se os monomios non son semellantes.
– Monomios semellantes: Súmanse ou réstanse os coeficientes e ponse a mesma parte literal.
Exemplo:
4x4 + 2x4+5x4 – 3x4 = (4+2+5-3) x4 = 8x4
– Monomios non semellantes: a suma ou resta déixase indicada, tal como está sen simplificala, quedando un polinomio cuxos termos son os monomios dados.
Exemplo: sumar os monomios 5x5, 3x4, 4x3, e restarlle os monomios 3x2, 6x.
Como os monomios non son semellantes non se poden sumar nin restar e, polo tanto, deixamos indicadas as operacións das que fala o exercicio, quedando 5x5 + 3x4 + 4x3 -3x2 - 6x.
- Multiplicación de monomios. Pódense multiplicar todos os monomios sexan ou non sexan semellantes.
O produto de dous ou máis monomios dá como resultado outro monomio que vai ter como coeficiente o produto dos coeficientes, e como parte literal a mesma, con expoñente a suma dos expoñentes.
Exemplo:
2x4·3x3·2x·(- 4x2) = [2·3·2·(-4)] x4+3+1+2 = -48 x10
- División de monomios. Pódense dividir todos os monomios sexan ou non sexan semellantes.
A división de dous monomios dá como resultado outro monomio que vai ter como coeficiente o cociente entre os coeficientes, e como parte literal a mesma, con expoñente a diferenza ou resta dos expoñentes. Para que o resultado sexa un monomio, o grao do numerador ten que ser maior ou igual que o grao do denominador.
Exemplo:
12 x6 : 4 x2 = = (12:4) x6-2 = 3 x4, é un monomio.
12 x2 : 4 x6 = = (12:4) x2-6 = 3 x - 4 = , non é un monomio, xa que o expoñente da parte literal non é un número natural
Actividade resolta
Fíxese nos resultados de facer as sumas, restas multiplicacións e divisións de monomios
| 2a -3b = 6 ab | 5a. 6 a2 = 30 a . a 2 = 30 a 3 |
| 5 x 2 y . ( -2 xy) = -10 x2 x y y= -10 x3 y 2 | 12 x5 : 4 x = 3 x5 : x = 3 x4 |
| 6x3 y2 _ 2 x y2 = 3 x3 y2 : xy2 = 3 x2 | -7x2 y3 : ( -2 xy) = 7/2 x y2 |
| 2 x y + 5x y = 7 x y | 2x2+9x2 = 11x2 |
| 3a - 8a = -5 a |
3x - 6 x2 queda como está, non son semellantes |
| 3/2 x2 y + 7/2 x 2 y = 10/2 x2 y = 5 x2 y |
2a b 2 - 4 a2 b queda como está, non son semellantes |
| 6 x 2 + 5 x2 + 2 x2 = 13 x2 |
2 ab + 5 a b + 4 b a - 2 a b - 3 b a = 6 a b |
| 5 c d2 + 5 c2 d - 3 c d2 = 2 c d2 - 5 c2 d |
2/3 x4 . 3/5 x2= 2/3 . 3/5 x4+2 = 6/15 x6 |
| 2x2. 3 x4 : 2 x3 = 6 x6 : 2 x3 = 3 x3 |
21x8 : 7 x5 = ( 21: 7) x8-5 = 3 x 3 |
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0