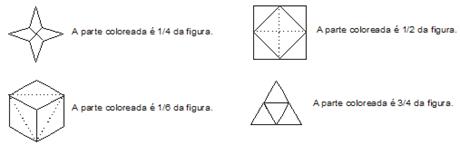
6.2 Solucións das actividades complementarias

Fraccións e números decimais

S24.

S25.

a) Hai ¾ do total, daquela falta ¼ para enchelo; a metade de ¼ é ¼ : 2 = 1/8. Por tanto hai no encoro

 b) Gastamos 1/5 de 7/8, isto é,

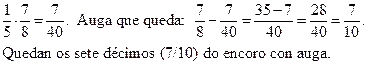
S26.

O luns vendéronse 1/3 de 300: multiplicamos 1/3 por 300 e dá 100 paquetes, daquela quedan 200 paquetes sen vender. O martes vendéronse a metade de 200, que son 100 paquetes, logo quedan outros 100 sen vender aínda. O mércores vendéronse 2/5 ·100 = 40 paquetes. Quedan finalmente sen vender 60 paquetes.

S27.

S28.

• 84/24 é redutible, pódese simplificar por 12, resultando 7/2.
• 47/49 non é redutible.
• 3003/1300 é redutible, pódese simplificar por 13, resultando a fracción 231/100.

S29.

Dividimos o intervalo de 0 a 1 en cinco partes, e sinalamos a terceira división (3 de 5):

S30.

Amplificamos as fraccións de xeito que teñan igual denominador, que é o mínimo común múltiplo de 3, 4, 5 e 2, que é 60. Daquela:

Agora ordenámolas segundo o valor dos numeradores:

   [O símbolo > significa “maior que”].

S31.

 S32.

2,07565656...	Decimal periódico mixto. O período é 56.
897,432155555...	Decimal periódico mixto. Período = 5.
120,9	Decimal exacto.
-4,102102102...	Decimal periódico puro. Período = 102.

 S33.

S34.

Sexa x o soldo mensual; os 2/3 de x son 600 euros, polo tanto:

S35.

Sexa x o número de lambetadas que hai na bolsa ao principio. Se comemos 2/3 das lambetadas, quedará aínda 1/3 delas. Daquela, 1/3 de x son 20, e:

S36.

Os alumnos do colexio son x; 3/8 de x son 192; daquela:

S37.

Na primeira hora camiñan 1/3 de 1050 metros. Multiplicamos 1/3 por 1050 e dá 350 metros. Para a segunda hora multiplicamos 4/15 por 1050 resultando 280 metros; e na terceira hora camiñan o que falta: 1050 m – 350 m – 280 m = 420 metros.

S38.

2/3 de 300 litros son 200 litros, que vendemos a 2 €, cobramos 400 euros. Dos 100 litros que sobran vendemos a quinta parte; 1/5·100 = 20 litros, a 3 € son 60 euros. Quedan aínda 80 litros, que vendemos a 1 €, así que cobramos 80 euros. Sumamos todos os euros: 400 € + 60 € + 80 € = 540 euros.

S39.

 

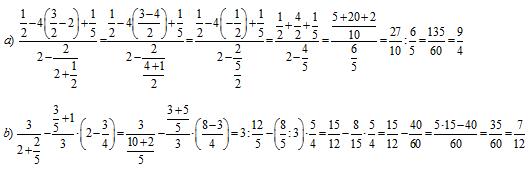
Mesturas

S40.         

Poden separarse por decantación as mesturas de auga e aceite e as de aceite con vinagre, xa que os líquidos son inmiscibles nos dous casos.

S41.

Utilizar un imán potente para atraer os obxectos de ferro; ou ben botar o lixo nun tanque de auga: o ferro afundirá e o papel máis o plástico aboiarán na superficie da auga.

S42.

Primeiro decantamos o aceite nun funil de decantación. Así separamos o aceite da auga salgada. Logo quentamos a auga salgada para evaporar a auga e no fondo do recipiente quedará o sal sólido.

S43.

Disolucións	Soluto	Disolvente
Mestura combustible para motos (gasolina + aceite)	Aceite (está en pouca cantidade)	Gasolina
Aceiro (ferro + carbono)	Carbono (compoñente minoritario)	Ferro
Alcohol de farmacia	Auga (ten un 4% nada máis)	Alcohol
Aire húmido	Auga	Aire

S44.

É unha substancia pura. En tanto que unha substancia está a ferver a temperatura non cambia; se fose unha mestura a temperatura aumentaría durante a ebulición.

S45.

Deterxente: é unha mestura; refresco: mestura; diamante: é carbono puro, é unha substancia pura; auga da billa: mestura (ten auga e sales minerais); ouro: substancia pura; augardente: mestura (alcohol, auga e outras moléculas).

S46.

O sulfato de cobre é máis soluble na auga quente que na fría. Se arrefriamos unha disolución saturada de sulfato de cobre, a cantidade de sal que pode estar disolvida diminúe e parte deste sal irá ao fondo do recipiente en forma de sólido insoluble.

S47.

Aceite, auga e sal	Primeiro decantar o aceite, logo evaporar a auga e quedará o sal no fondo do vaso.
Etanol, auga e azucre	Primeiro destilar o líquido, así separamos o alcohol xa que ferve a temperatura máis baixa que a auga; logo evaporamos a auga, quedará azucre sólido no recipiente.
Area, vinagre e sal	Primeiro filtramos a disolución, a area queda retida no filtro; logo quecemos para evaporar a auga e o vinagre, quedará o sal no fondo.

S48.

Afirmación	V / F
Non se pode disolver un gas en auga.	Falso.
Nunha disolución acuosa o disolvente ten que ser auga.	Falso; a auga pode ser tamén o soluto
Todas as disolucións conteñen auga.	Falso.
O soluto disólvese, o disolvente non.	Falso. Mestúranse entre si os dous compoñentes da disolución.

Concentración das disolucións

S49.

S50.

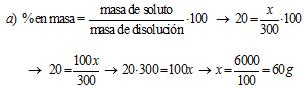
b) 300 g de xarope – 60 g de azucre= 240 g de auga.

S51.

Afirmación	V / F	Razoamento
200 g da disolución teñen 200 g de auga	Falso	200 g de disolución teñen 200.20% = 40 g de soluto e 160 g de auga.
En 500 g da disolución hai 100 g de soluto	Verdadeiro	En 500 g da disolución hai 500.20% = 100 g de soluto. Pódese calcular tamén por regra de tres:
Nun quilogramo da disolución hai 800 g de auga.	Verdadeiro	En 1000 g de disolución hai 1000.20% = 200 g de soluto e o resto, 800 g, de auga.

S52.

S53.

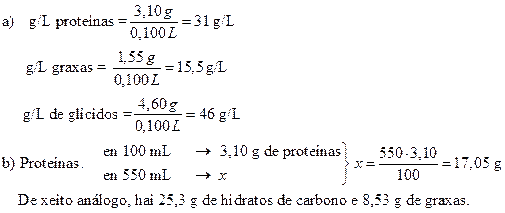
S54.

Cambiamos as unidades de miligramos a gramos, e de mililitros a litros:

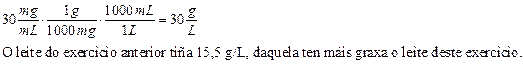
S55.

• En miligramos de soluto por cada litro de disolución.
• Porque teñen pouco fluoruro.
• Se nun litro hai 0,5 mg de calcio, en 1,5 litros (regra de tres) hai 0,75 mg. De bicarbonato hai 6,9 gramos.
• É a masa sólida que queda logo de evaporar toda a auga.
• 

S56.

a) Unha disolución; supoñemos que o leite é totalmente soluble na auga.

b) O biberón contén 180 g de auga + 6·3,6 g de leite = 180 g de auga + 21,6 g de leite = 201,6 g de disolución. Se en 201,6 g de biberón hai 21,6 gramos de leite, en 160 g de biberón (regra de tres) hai 17,1 gramos de leite.

S57.