6.1 Solucións das actividades propostas

S1.

Mediante puntos	As esquinas dun obxecto, o punto onde pendura un cadro, unha lámpada, etc
Mediante rectas	As arestas dun obxecto, dun edificio ou dun cuarto, os bordos dunha porta, dunha ventá, dunha mesa, dun folio, etc
Mediante planos	A superficie das paredes ou do chan dun cuarto, a superficie dunha mesa, o cristal dunha ventá, etc

S2.

Puntos: as esquinas do moble e dos caixóns, os buratos dos parafusos que suxeitan os tiradores, etc
Rectas: as arestas dos taboleiros que forman o moble, dos caixóns, etc
Planos: as superficies dos taboleiros que forman o moble, do taboleiro do fondo, etc.

S3.

Trace algunhas rectas que pasen polo punto P e que corten a recta r. Cantas se poden trazar?	Pódense trazar infinitas rectas que pasen polo punto P e corten a recta r.
Trace agora rectas paralelas a r que pasen polo punto P. Cantas se poden trazar? E rectas paralelas a r que pasen por P?	Polo punto P soamente se poden trazar unha recta paralela e unha recta perpendicular á recta r.

S4.

Nome das dúas rúas paralelas máis próximas á rúa Corcubión	Avenida das Conchiñas e a rúa Alcalde Lens.
As rúas Barcelona e Alcalde Lens son perpendiculares?	Si, sono.
As rúas Gramela e Andrés Gaos son secantes?	Si, sono.
As rúas Gramela e Andrés Gaos son perpendiculares?	Non, son secantes.

S5.

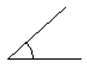
	Aproximadamente 42º
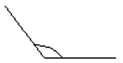
	Aproximadamente 127º
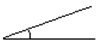
	Aproximadamente 20º
	Aproximadamente 158º
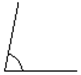
	Aproximadamente 80º

S6.

a	25º 40’ 35’’ + 70º 8’ 30’’ =	95º 49´ 5”
	15º 25’ 40’’ + 24º 50’ 30’’ =	40º 16´10”
	10º 20’ 40’’ + 42º 50’ 52’’ + 28º 45’’ =	81º 12´17”
b	130º 40’ 25’’ - 75º 30’ 40’’ =	55º 9´ 45”
b	85º 18’ 30’’ - 60º 50’ 22’’ =	24º 28´8”
c	15º 25’ 30’’ x 3 =	46º 16´30”
c	40º 35’ 50’’ x 4 =	162º 23´20”

S7.

Recto.
180º
Obtuso.
180º
Complementarios.
Consecutivos.
Consecutivos / 180º
Iguais.

S8.

Cantos graos miden tres ángulos rectos?

90º x 3 = 270º

E medio ángulo recto?

90º : 2 = 45º

Cantos ángulos rectos son 360º?

360º : 90º = 4 ángulos rectos.

S9.

Dor de cabeza	Inmaterial	Aire	Material
Roupa	Material	Sede	Inmaterial
Auga	Material	Area	Material
Envexa	Inmaterial	Alegría	Inmaterial
Libro	Material	Sur	Inmaterial
Beleza	Inmaterial	Osíxeno	Material

S10.

Que instrumento utilizaría ?	Unha regra ou unha cinta métrica.
Que propiedade xeral está a medir?	A lonxitude
En que unidades tería que expresar a medida se no SI?	Metro
Que outras unidades de medida podería utilizar?	Centímetros, milímetros

S11.

Magnitude	Fundamental / Derivada	Escalar / Vectorial
Masa	Fundamental	Escalar
Lonxitude	Fundamental	Escalar
Tempo	Fundamental	Escalar
Superficie	Derivada	Escalar
Volumen	Derivada	Escalar
Densidade	Derivada	Escalar

S12.

km	m	dm	cm	mm
0, 000325	0, 325	3, 25	32, 5	325
0, 00127	1, 27	12, 7	127	1270
0, 013	13	130	1300	13000
0, 009	0, 9	9	90	900
5 000	5 000 000	50 000 000	500 000 000	5 000 000 000

S13.

	Múltiplo e submúltiplo		Múltiplo e submúltiplo
Balea (30 m)	3 dam	Bacteria (0, 00005 m)	0, 05 mm
Mesa (0, 75 m)	75 cm	Lapis (0, 15 m)	15 cm
Montaña (3500 m)	3, 5 km	Home (1, 80 m)	180 cm

S14.

A superficie é unha magnitude derivada por que se obtén de multiplicar dúas lonxitudes

S15.

Para calcular a superficie do campo hai que multiplicar o longo e largo do cuarto; S = 20m x 65 m = 1 300 m²;
O campo de deportes terá unha superficie de 1 300m².

S16.

2 500 mg

0, 25 dag

0, 0025 kg

S17.

Para pasar a masa de 2,5 a quilogramos debemos multiplicar por 1000, xa que unha tonelada ten 1.000 kg;
2,5 · 1.000 = 2.500 kg.
Daquela, 2,5 toneladas corresponden a 2.500 quilogramos

S18.

285 K

T_c=T_k– 273

Tc = 285- 273 = 12 ºC

254 K

T_c=T_k– 273

Tc = 254 - 273 = - 19 ºC

S19.

Para sabermos os segundos que ten unha hora primeiro debemos indicar os minutos que ten unha hora e a continuación multiplicar polos segundos que ten cada minuto; 60 minutos. 60 segundos = 3.600 segundos.
Así un día terá 3.600 segundos.
Para sabermos os segundos que ten un día, temos que multiplicar o número de horas dun día polo número de segundos dunha hora; 3.600 segundos. 24 horas = 86.400.
Polo tanto un día terá 86.400 segundos.

S20.

O volume da rocha será a diferenza entre o volume da probeta coa rocha mergullada e o volume da probeta sen a rocha; é dicir V= 7 ml – 5 ml = 2 ml
O volume da rocha será de 2 ml.

S21.

Para calcularmos o volume de aire temos que multiplicar o longo, largo e alto do cuarto;
V= 4m x 3 m x 2, 5 m = 30 m³
O volume de aire do cuarto é de 30 m³

S22.

É máis doado flotar no mar, porque a auga salgada é de maior densidade.

S23.

A densidade é a relación entre a masa dun corpo e o volume que ocupa;

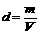
A densidade é inversamente proporcional ao volume.
Ten unha maior densidade o chumbo, xa que 1 kg de chumbo ocupa menos volume ca mesma masa de palla.

S24.

Afirmación	V / F
Os líquidos teñen forma definida	F
As partículas dos gases non se moven	F
Os gases non ocupan espazo	F
As partículas dos líquidos gozan de grande mobilidade	V
Os líquidos e os gases móvense con dificultade polo interior das tubaxes	F

S25.

As partículas que forman o fume, ao estaren en estado gasoso, móvense independentemente unhas das outras, e expándense, é dicir, ocupan todo o espazo que poden, repartíndose na habitación de xeito uniforme.

S26.

As frechas vermellas representan cambios por quecemento, entanto que as azuis por arrefriamento.

S27.

A roupa seca, ao sol	Vaporización
Cando a lava arrefría, pasa a rocha sólida	Solidificación
Un vaso con auga que sacamos do frigorífico, ao cabo dun rato está mollado por fóra	Condensación
Ao abrir un frasco de perfume apréciase o aroma en todo o cuarto	Vaporización
O vapor de auga das nubes que produce as choivas	Condensación
O desxeo das montañas	Fusión
Un espello que se empapa ao botarlle o alento	Condensación

S28.

Sangue

Mestura

Limoada

Mestura

Aire

Mestura

Osíxeno

Pura

S29.

Mestura homoxénea

tortilla

Mestura heteroxénea

leite

Mestura homoxénea

S30.

Materia prima	madeira, arxila, calcaria, cuarzo, la de ovella, pirita (mineral de ferro), látex
Material elaborado	taboleiro aglomerado, pasta de porcelana, cemento, vidro, fío de la, bloque de ferro, caucho
Produto	moble, obxecto decorativo, formigón, lente, prenda de vestir, ferramenta, pneumático

S31.

As fibras artificiais sintéticas (poliamida, poliéster, poliuretano, etc.) obtéñense quimicamente a partir de materias primas moi variadas (carbón, alcatrán, amoníaco, petróleo, etc.) mediante un proceso chamado polimerización. Os produtos obtidos por este procedemento reciben o nome de polímeros e utilízanse, ademais de para a fabricación de tecidos, na elaboración de plásticos, produtos estruturais para resistir esforzos (parachoques de automóbiles, tubaxes...), illantes, filtros, etc.

Se observa a etiqueta dalgunhas prendas de vestir pode comprobar que a maioría delas utiliza fibras artificiais na súa composición.

Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0

« Anterior | Seguinte »