2.8.5 Aplicacións: resolución de problemas cotiáns
Os triángulos semellantes permiten a resolución dunha enorme cantidade de problemas relacionados coa vida cotiá. A clave da súa resolución está na identificación dos propios triángulos semellantes.
Actividade resolta
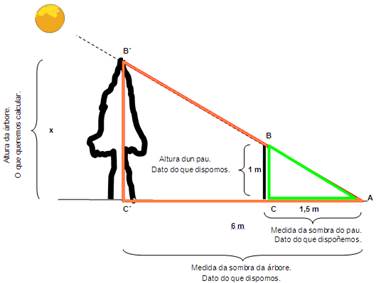
Podemos calcular a altura dunha árbore medindo a lonxitude da súa sombra e comparándoa coa lonxitude da sombra dun obxecto coñecido.
Actividades propostas
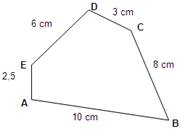
S30.Comprobe que nas figuras seguintes o cociente entre os lados correspondentes é o mesmo e, aínda así, as figuras non son semellantes. Por que?

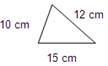
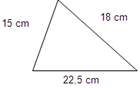
S31. Comprobe se son semellantes os seguintes triángulos.
S32. A medida de dous lados dun triángulo é de 12 cm e 15 cm. O ángulo formado por eles é de 40º. Outro triángulo ten un lado de 8 cm e un ángulo de 40º nun dos seus extremos. Cal ten que ser a medida do outro lado do ángulo para que o triángulo sexa semellante ao primeiro?
S33. Constesta as seguintes cuesitons
1. Nas tuas propias palabras como describirías aos triángulos que se te presentan na figura.
2. Como relacionarías os lados correspondientes coñecendo os ángulos.
3. Como relacionarías os ángulos coñecendo os ángulos.
4. Como describirías unha simboloxía que axude a representar dous triángulos semellantes.
5. Para que dous triángulos sexan congruentes, como debe ser a razón de semellanza.
6. Realiza varios cambios nas figuras e determina a razón de semellanza, explica coas tuas palabras que e a razón de semellanza.
7. Como son os ángulos en triángulos semellantes.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0