2.7 Teorema de Pitágoras

O teorema de Pitágoras establece una relación entre certos tipos de triángulos e os seus lados. Este tipo de triángulos chámase rectángulo, por medir un dos seus ángulos 90º, o que significa que é un ángulo recto.

Antes de enunciar este teorema imos lembrar os tipos de triángulos que existen segundo sexan os seus lados e os seus ángulos.

Clasificación segundo os seus lados
Equilátero	Tres lados iguais
Isóscele	Dous os lados iguais.
Escaleno	Tres lados desiguais.

Clasificación segundo os seus ángulos
Acutángulo	Ten todos os seus ángulos menores a 90°
Rectángulo	Ten un ángulo recto, mide 90°
Obtusángulo	Ten un ángulo maior de 90°

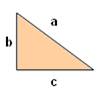
Nun triángulo rectángulo o lado de maior lonxitude chámase hipotenusa, e os outros dous, de menor lonxitude e perpendiculares entre si, catetos.

Lembre que en calquera triángulo, a suma das medidas dos tres ángulos vale 180º. Polo tanto, en calquera triángulo rectángulo, a suma dos dous ángulos agudos é 90º.

Pitágoras foi un filósofo e matemático grego que viviu cara ao ano 500 antes de Cristo. El e os seus discípulos demostraron a relación entre os catetos e a hipotenusa dun triángulo rectángulo. É dicir:

Nun triángulo rectángulo, o cadrado da hipotenusa é igual a suma dos cadrados dos catetos.

Hipotenusa = a              catetos = b, c

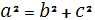Para vermos que é certo, e sempre nun triángulo rectángulo, analizamos este curioso quebracabezas:

Observe que os dous cadrados grandes son iguais. Se a cada un deles lle suprimimos catro triángulos iguais de lados a, b e c, queda a² no primeiro, b² + c² no segundo. Daquela, ha ser a² = b² + c²