3.4 Proporcionalidade composta

Unha proporcionalidade é composta se interveñen máis de dúas magnitudes proporcionais. Para resolver problemas de regra de tres composta aplícase o seguinte procedemento:

• Identifícanse as magnitudes que interveñen, colócanse os datos e a incógnita, e determínase a relación de proporcionalidade entre cada magnitude e a da incógnita.

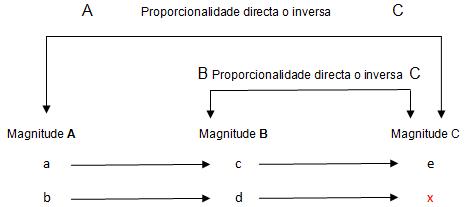
• Formúlase a proporción, coa razón directa ou inversa segundo as magnitudes sexan directa ou inversamente proporcionais, e resólvese.

Actividade resolta

Un gandeiro necesita 600 kg de penso para alimentar corenta vacas durante oito días. Durante cantos días poderá alimentar vinte vacas con 1.500 kg de penso ?

• a) Colócanse os datos e determínase a relación de proporcionalidade

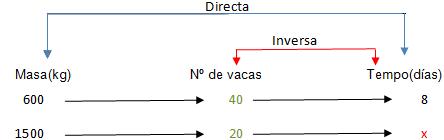
• b) Fórmase a proporción:

Multiplícanse as razóns das cantidades da mesma magnitude, pondo a razón inversa se a proporcionalidade é inversa,e iguálanse coa razón das cantidades da incógnita.

Magnitudes que non son proporcionais

Non sempre as magnitudes son directa ou inversamente proporcionais entre si; hai moitas outras relacións de dependencia. Así, a forza coa que se atraen gravitacionalmente dous corpos (a Terra e o Sol, por exemplo) diminúe coa distancia, pero se a distancia aumenta ao dobre a forza non diminúe á metade, logo non son inversamente proporcionais (de feito a forza faise catro veces menor).

Outro exemplo témolo nos impostos que pagamos á Facenda: se unha persoa gaña 1.000 euros ao mes e outra gaña 4.000 euros, o imposto do IRPF que paga esta última non é catro veces maior.

Un derradeiro exemplo é o crecemento exponencial de bacterias e mesmo, ás veces, da poboación humana: se nun tempo dado a poboación aumenta unha certa cantidade, nun tempo dobre a poboación aumenta sete veces máis aproximadamente: non son proporcionais.