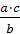3.3 Magnitudes inversamente proporcionais.

Dúas magnitudes son inversamente proporcionais se un aumento ou unha diminución nunha das magnitudes determina unha diminución ou un aunmento proporcional na outra.

Vexamos un exemplo de dúas magnitudes inversamente proporcionais: velocidade dun automóbil e tempo transcorrido en percorrer unha distancia de 120 km. Observamos na táboa como á medida que aumenta unha das magnitudes diminúe proporcionalmente a outra:

Velocidade (km/h)	30	40	60	120	···
Tempo transcorrido (horas)	4	3	2	1	···

Na táboa observase o seguinte:

• A razón de dúas cantidades calquera da primeira magnitude (velocidade) e a razón inversa das correspondentes cantidades da segunda magnitude (tempo) forman unha proporción

 

• Que o produto das cantidades dunha magnitude (velocidade) polas correspondentes da outra é sempre o mesmo número, é unha constante, coñecida como constante de proporcionalidade inversa:

30 · 40 = 40 · 3 = 60 · 2 = 120 · 1 = 120 = K (constante de proporcionalidade inversa)

 

Proporcionalidade inversa

A resolución de problemas típicos de proporcionalidade inversa pódese facer mediante dúas estratexias:

Regra de tres simple inversa

A regra de tres simple inversa é o procedemento para calcular unha cantidade que forma proporción con outras tres cantidades coñecidas de dúas magnitudes inversamente proporcionais.

Para resolver os problemas podemos seguir o seguinte esquema:

Colócanse os datos e determínase se a proporcionalidade é inversa:

Fórmase a proporción na que a razón das cantidades da magnitude A aparece invertida:  =                  x =

 

Redución á unidade

Fíxese no exemplo que aparece nesta páxina a modo de actividade resolta. Nese caso, reducir á unidade é determinar cantos días pode comer un animal:

20 animais · 60 días = 1 animal · 1.200 días

Daquela, se un animal pode comer 1.200 días, 30 animais poderán comer 30 veces menos días:

 

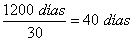
Pero tamén podemos formulalo do seguinte xeito:

Número de animais	1	20	30
Número de días	x	60	?

Como as dúas magnitudes son inversamente proporcionais, o produto das cantidades correspondestes é constante: 20 · 60 = 1 · x = 1.200.

Daquela, se un animal pode comer 1.200 días, trinta animais han comer trinta veces menos.

 

 

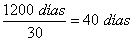
Actividade resolta

Un gandeiro ten herba almacenada para alimentar vinte animais durante sesenta días. Se compra dez animais máis, para cantos días terá herba suficiente?

 

1	Razoamos o problema	Se 20 animais poden comer 60 días, daquela 30 animais comerán x días
2	Resumimos o anterior así	20 animais ———— 60 días 30 animais ———— x días
3	Determínase se a proporcionalidade é inversa	Razoamos: se para 20 animais a herba almacenada nos dá para 60 días, se aumentamos o número de animais, a outra magnitude (o número de días), tendo a mesma herba almacenada, terá que diminuír. Xa que logo é inversa.
4	Escribimos unha proporción coa primeira razón invertida	=
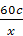
5	Despexamos x e calculamos	30·x =20·60 ; x= 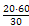=40 días