3.1 Razón e proporción de números

Razón

Unha razón é a división ou cociente entre dous números ou dúas cantidades comparables entre si.

Represéntase , e lese "a é a b"

Os termos dunha razón chámanse antecedente e consecuente. O antecedente é o dividendo ou numerador, e o consecuente é o divisor ou denominador.

• Exemplo 1: nun concurso no que hai tres premios, participan 21 persoas. Podemos expresar matematicamente a relación anterior mediante unha razón entre o número de premios e o número de participantes, e queda:

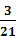
• Exemplo 2. Temos dous sacos de cemento; o saco grande pesa 7,5 kg e o pequeno pesa 2,5kg.

A razón entre a masa do saco grande e a do saco pequeno é  , o que quere dicir que o saco grande ten tres veces a masa do pequeno.

 

Non debe confundir unha razón cunha fracción. Nos dous exemplos anteriores vemos como os termos antecedente e consecuente dunha razón poden ser números enteiros ou números decimais. Nunha fracción os seus termos ,numerador e denominador deben ser números enteiros.

Proporción

Unha proporción é una igualdade de dúas razóns.

Represéntase  , e lese "a é a b como c é a d"

 

Os termos dunha proporción :  

 

 Propiedades das proporcións

 a) En toda proporción, o produto de medios é igual ao produto de extremos:

             ó        a.d = b.c

 

• b)Nunha proporción, sempre, a razón entre a suma dos antecedentes e a suma dos consecuentes é igual á unha calquera das razóns:

 

 Exemplo:

 Sexa a proporción   comprobemos como se cumpren as propiedades anteriores:

 a)        ó     a.d = b.c     é dicir 2.6 = 4.3; 2 = 12

b)     é dicir     

 

 Cálculo dun termo descoñecido dunha proporción

 Para calcular o termo descoñecido nunha proporción,coñecendo os outros tres, aplícase a propiedade:

Produto de medios = produto de extremos

A ese termo descoñecido chámaselle cuarto proporcional.

ó  a.x=b.c    ó  

 

Observe que, considerando os catro elementos da proporción nos extremos dos brazos dunha aspa, podemos dicir que para calcular o termo descoñecido dunha proporción se multiplican os dous números coñecidos que forman un dos brazos da aspa e o resultado divídese polo terceiro número, emparellado coa incógnita no outro brazo.