3.2 Magnitudes directamente proporcionais
Unha magnitude é calquera propiedade física que poida ser medida: a lonxitude, a temperatura, os cartos, a masa, o tempo, etc. A dor, o amor e a ledicia poden ser grandes ou pequenas, pero non se poden medir, logo non son magnitudes.
Dúas magnitudes son directamente proporcionais se ao multiplicar (ou dividir) unha delas por un número a outra queda multiplicada (ou dividida) por ese mesmo número.
Vexamos un exemplo de dúas magnitudes directamente proporcionais: lonxitude dun tecido e o seu valor.
-
-
Cantidade de tecido (metros)
1
2
3
4
5
···
-
Prezo (euros)
6
12
18
24
30
···
-
Na táboa observase o seguinte:
-
A razón de dúas cantidades da primeira magnitude e a razón das correspondentes cantidades da segunda magnitude forman unha proporción:
![]()
-
Que os valores dunha magnitude son proporcionais aos valores correspondentes da outra; é dicir, forman unha serie de razóns iguais:
![]()
A constante de proporcionalidade directa é o valor que se obtén ao dividir calquera valor da segunda magnitude entre o correspondente da primeira. No noso exemplo K = 6.
-
A dobre número de metros correspóndelle dobre cantidade de euros; a triplo número de metros o triplo número de euros.
Proporcionalidade directa
A resolución de problemas típicos de proporcionalidade directa pódese facer mediante dúas estratexias:
Regra de tres simple directa
A regra de tres simple directa é un procedemento que ten por obxecto atopar unha proporción na que se coñecen tres cantidades de dúas magnitudes. É dicir, é un procedemento para atopar o cuarto proporcional.
Para resolver os problemas podemos seguir o seguinte esquema:
|
Colócanse os datos e determínase se a proporcionalidade é directa:
|
Fórmase a proporción e calcúlase o cuarto proporcional:
|
Redución á unidade
O método de redución á unidade consiste en:
1. Calcular primeiro o valor asociado á unidade na táboa de magnitudes proporcionais correspondente.
2. Coñecendo o dato do valor asociado á unidade, calcúlase o valor desexado.
Exemplo: para facermos tres traxes necesitamos 7,50 metros de tecido. Canto tecido usaremos para coser oito traxes.
|
1 |
3 |
8 |
|
? |
7,5 |
? |
– Calculamos os metros necesarios para facer un traxe.
![]()
– Coñecido o valor para unidade, neste caso un traxe, calcúlase para o valor desexado:
Para oito traxes: 8 traxes · 2,5 m/traxe = 20 metros.
Actividade resolta
Para facermos tres traxes necesitamos 7,50 metros de tecido. Canto tecido usaremos para coser oito traxes?
-
1
Razoamos o problema
Se para facer tres traxes necesitamos 7,5 metros de tecido, daquela para facer oito traxes necesitaremos x metros.
2
Escribimos o anterior así
3 traxes ———— 7.5 metros
8 traxes ——— x metros
3
Determinamos se a proporcionalidade é directa
Razoamos: se para tres traxes necesitamos 7.5 metros, se
aumentamos o número de traxes, a outra magnitude (os metros de tecido) tamén terá que aumentar. Xa que logo, é directa.
-
4
Escribimos unha proporción cos termos anteriores:

5
Despexamos x e calculamos:
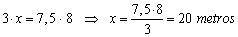
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0

 =
=  x=
x=