Glosario
Corda de circunferencia
-
Definición:
-
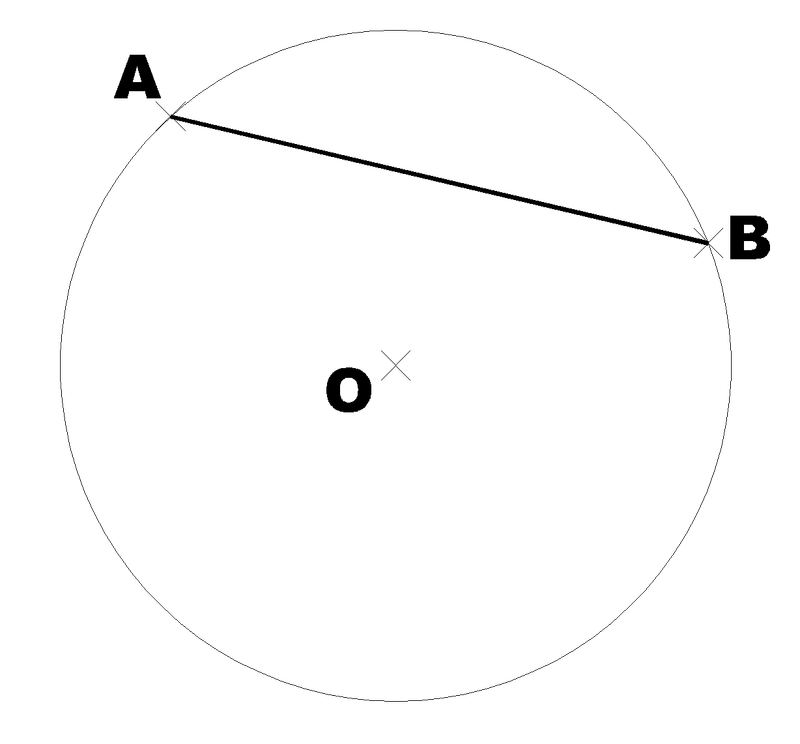
Unha corda é un segmento de liña recta que une dous puntos calquera dunha circunferencia sen pasar necesariamente polo centro. É importante distinguila do diámetro, que si o fai.
-
Exemplo:
-
Na imaxe, a liña que une A e B.
Diámetro
-
Definición:
-
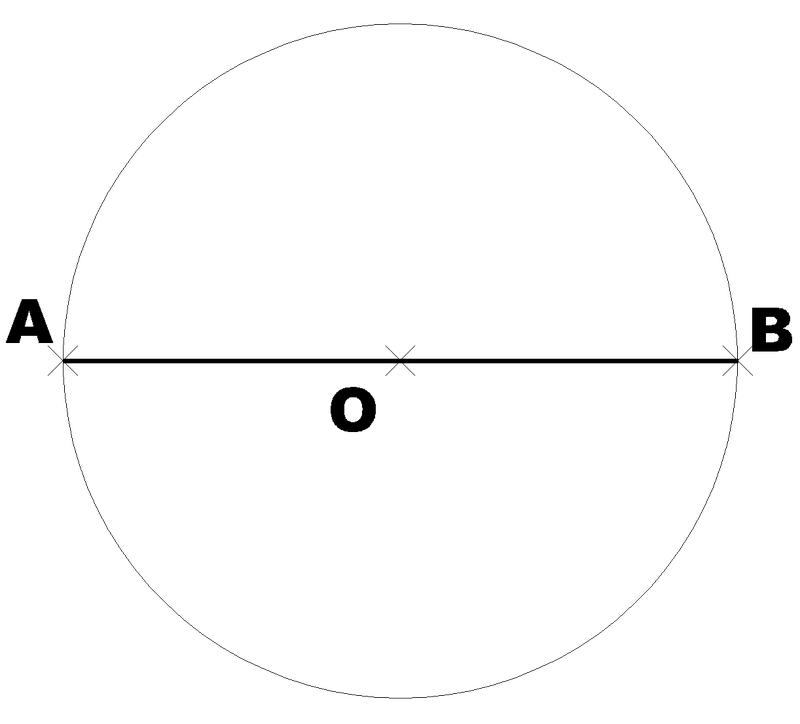
O diámetro é unha corda especial que pasa polo centro da circunferencia e divídea en dúas partes iguais. É o segmento máis longo que pode trazarse no interior dun círculo.
-
Exemplo:
-
Na imaxe, a liña que une A e B.
Radio
-
Definición:
-
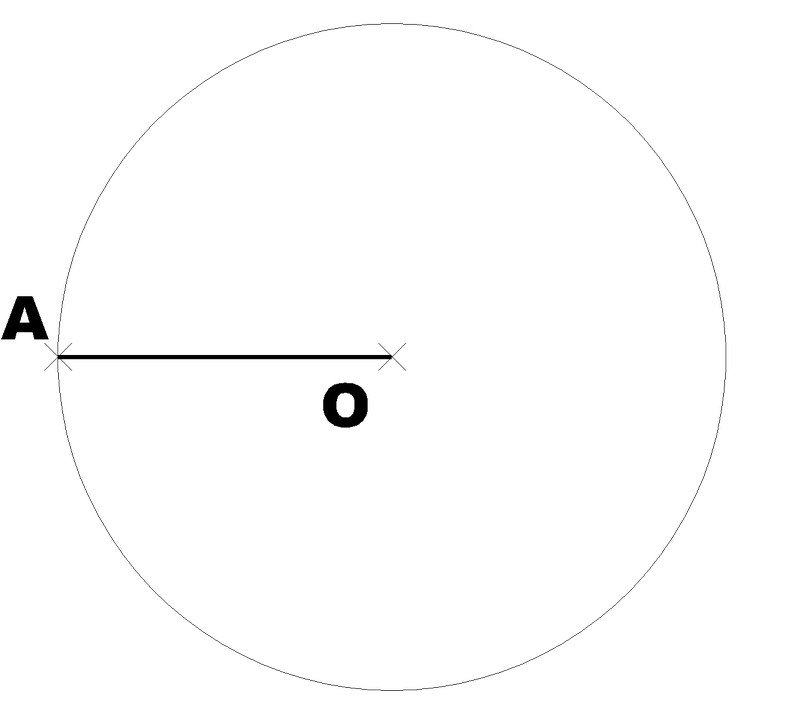
O radio é o segmento que une o centro dunha circunferencia con calquera punto da mesma. É a metade do diámetro.
-
Exemplo:
-
Na imaxe, a liña que une A e O.
Lado

-
Definición:
-
En xeometría plana, un lado é cada un dos segmentos que forman un polígono. Por exemplo, un triángulo ten tres lados, un cadrado ten catro etc.
-
Exemplo:
-
Na imaxe, as liñas nomeadas a, b e c.
Vértice

-
Definición:
-
Un vértice é o punto onde se atopan dous lados (nun polígono) ou tres ou máis arestas (nun poliedro).
-
Exemplo:
-
Na imaxe, os puntos A, B e C.
Poliedro
-
Definición:
-
Un poliedro é unha figura xeométrica tridimensionais cuxas superficies (caras) son polígonos planos.
-
Exemplo:
-
Pode ter diferentes formas, como o cubo, o tetraedro ou o dodecaedro.
Aresta

-
Definición:
-
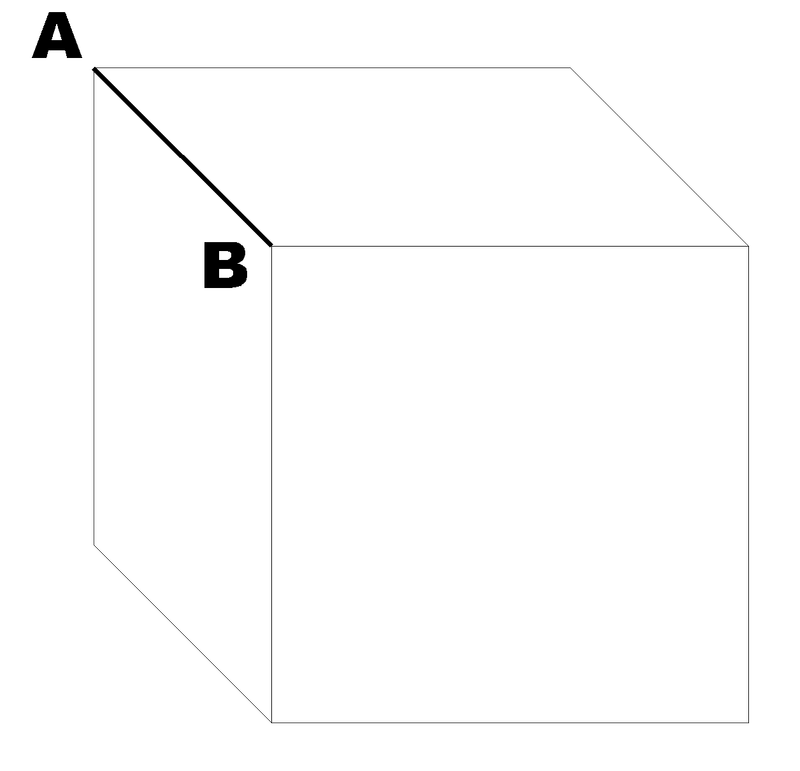
A aresta é o equivalente tridimensional ao lado: é o segmento que une dous vértices nunha figura tridimensional (como un poliedro). As arestas son as liñas onde se atopan dúas caras.
-
Exemplo:
-
Na imaxe, a liña que une A e B.
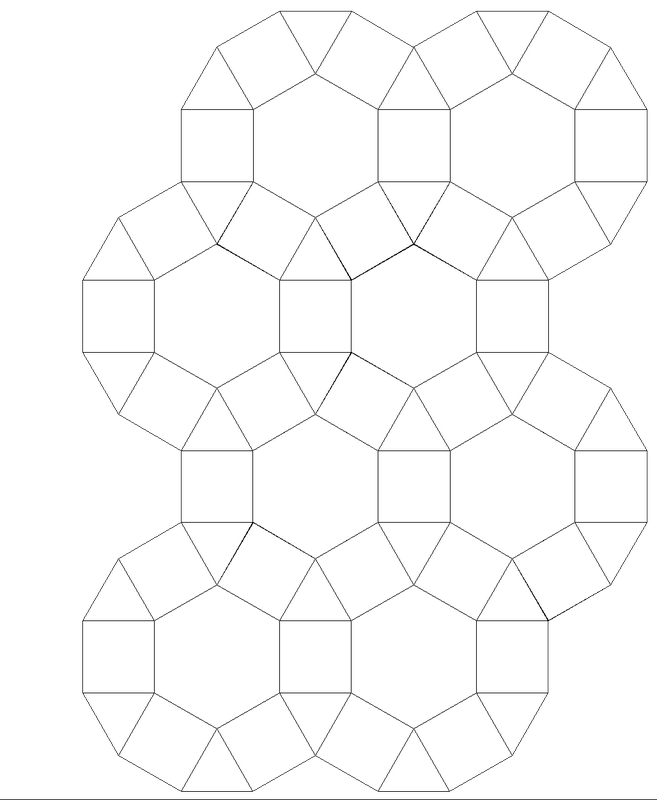
Teselado
-
Definición:
-
Un teselado é unha repetición ordenada dunha ou varias formas xeométricas que cobren completamente un plano sen deixar ocos nin solaparse.
-
Exemplo:
-
Son frecuentes na arte islámica, en mosaicos romanos e na arte contemporánea (como nas obras de Escher).
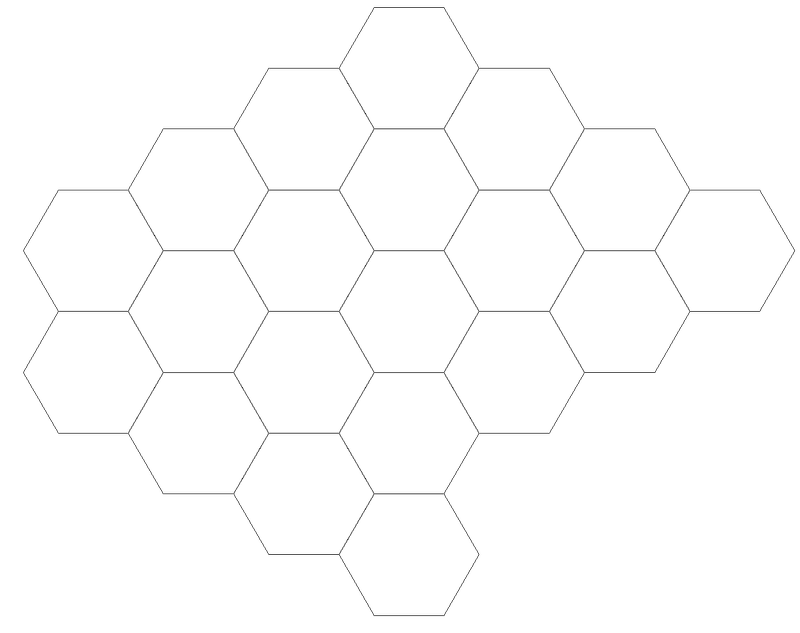
Rede modular
-
Definición:
-
Unha rede modular é unha estrutura organizada e repetitiva que se basea nunha unidade básica (o módulo), repetida de maneira ordenada no espazo, xa sexa bidimensional ou tridimensional.
-
Exemplo:
-
Un panal de abellas é unha rede modular de hexágonos.
 Todos os seus lados son iguais.
Todos os seus lados son iguais. Ten dous lados iguais e un desigual.
Ten dous lados iguais e un desigual. Os tres lados son desiguais.
Os tres lados son desiguais. Ten un ángulo recto, é dicir, de 90 graos.
Ten un ángulo recto, é dicir, de 90 graos.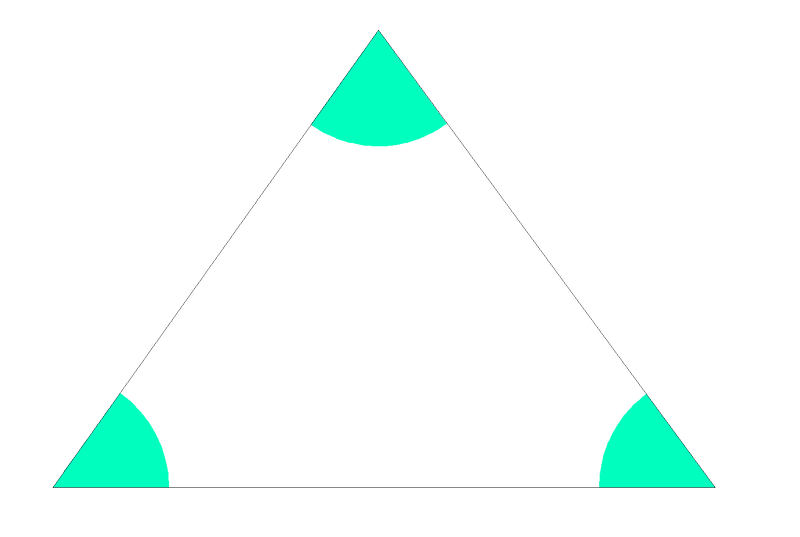 Todos os seus ángulos son menores de 90 graos.
Todos os seus ángulos son menores de 90 graos. Ten un ángulo maior de 90 graos.
Ten un ángulo maior de 90 graos.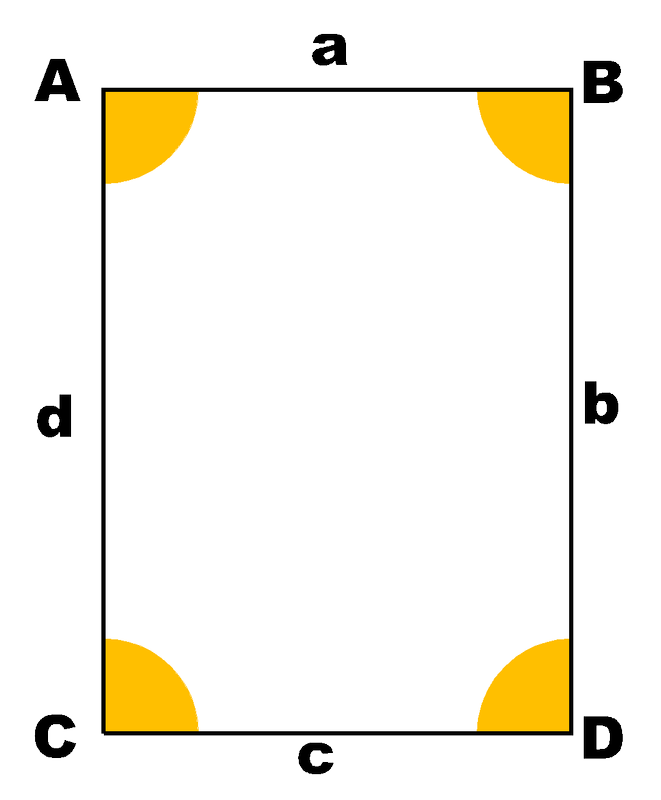 - Lados opostos iguais.
- Lados opostos iguais.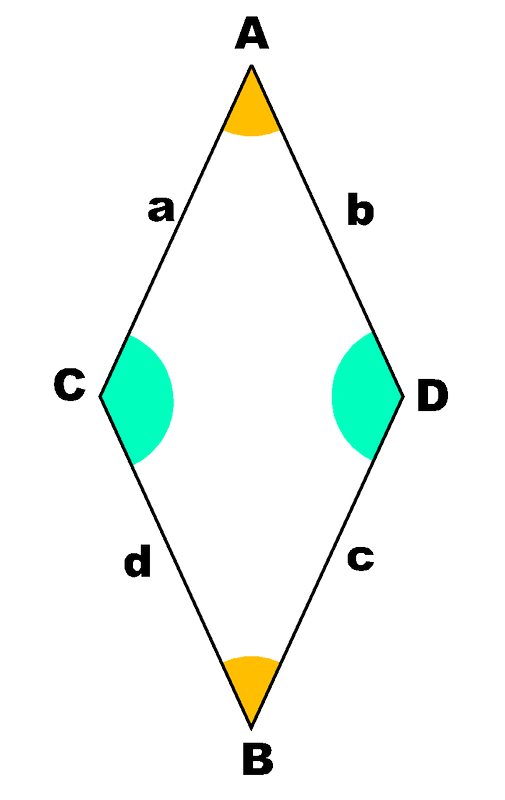 - 4 lados iguais.
- 4 lados iguais.  - Lados opostos iguais e paralelos.
- Lados opostos iguais e paralelos.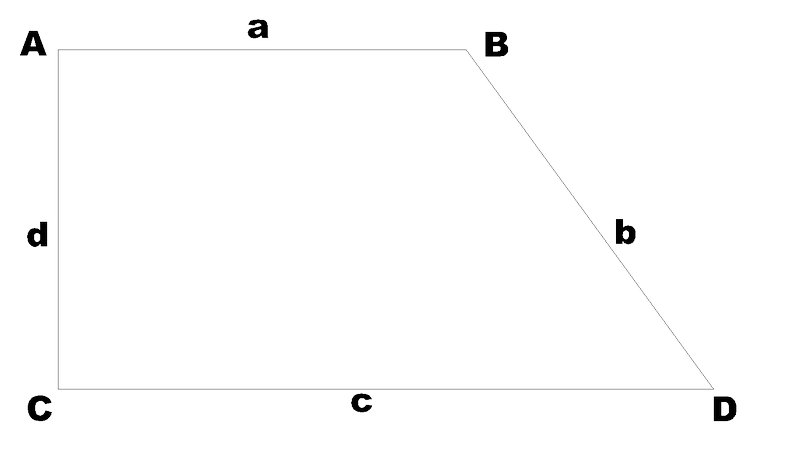 - Un ángulo recto.
- Un ángulo recto. 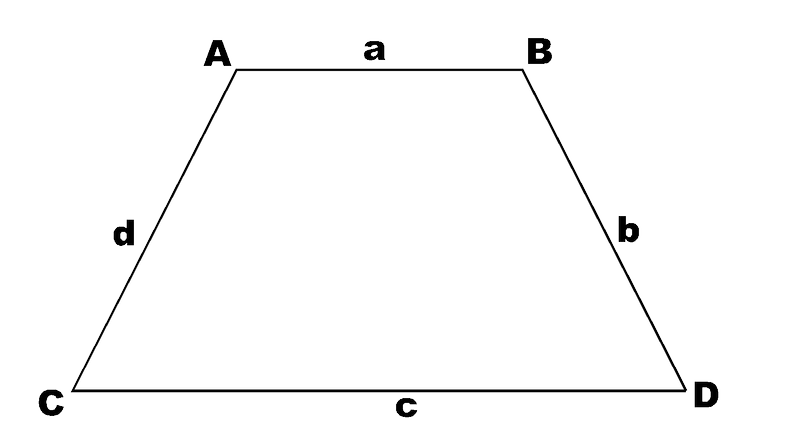 - Un par de lados paralelos.
- Un par de lados paralelos.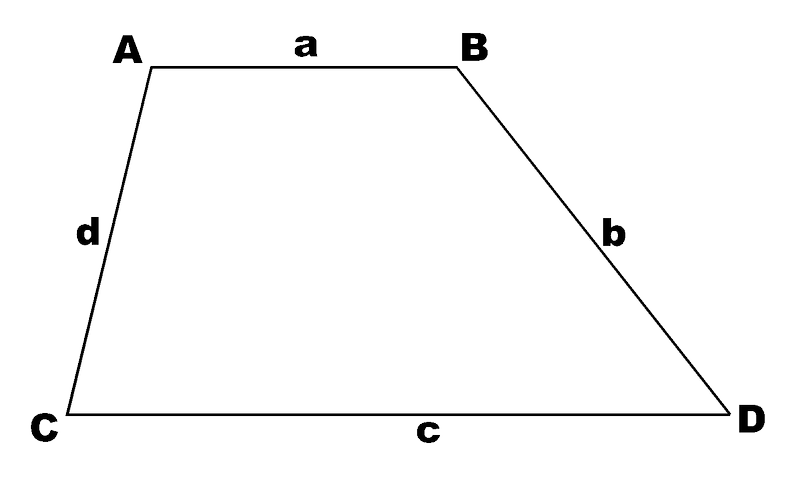 - Ningún lado igual (agás os paralelos).
- Ningún lado igual (agás os paralelos). 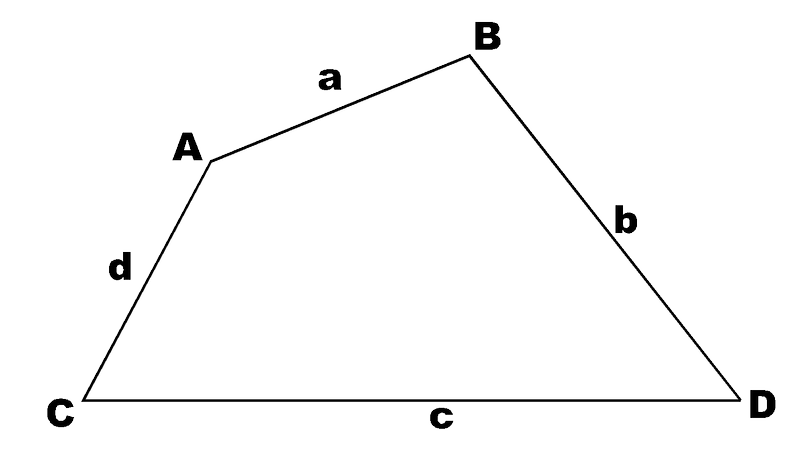 Non teñen lados paralelos.
Non teñen lados paralelos.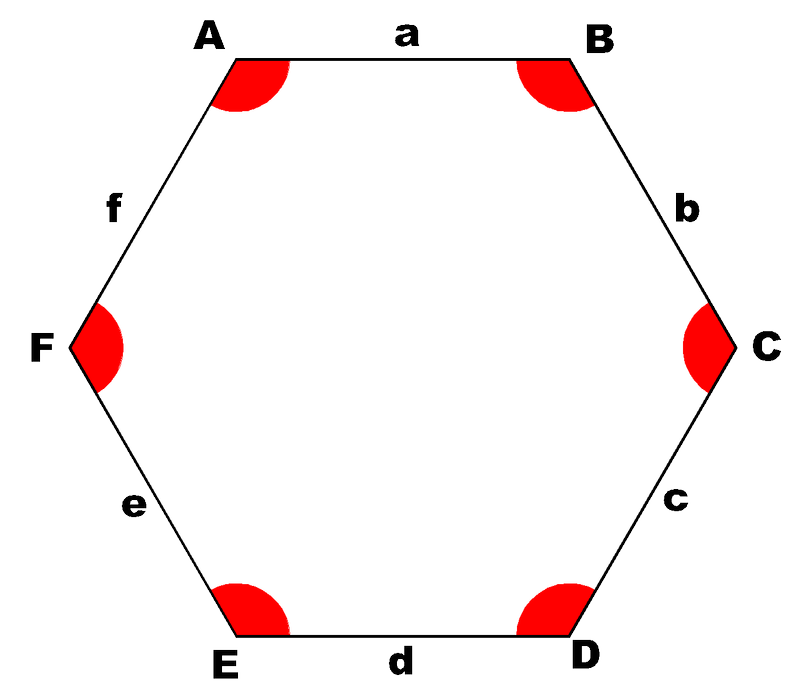 hexágono ten seis lados. É moi especial porque se adapta perfectamente para cubrir espazos sen deixar ocos, por iso atopámolo en paneis de abellas, baldosas e deseños modernos.
hexágono ten seis lados. É moi especial porque se adapta perfectamente para cubrir espazos sen deixar ocos, por iso atopámolo en paneis de abellas, baldosas e deseños modernos.