Glosario
Glosario
Ángulo
-
Definición:
-
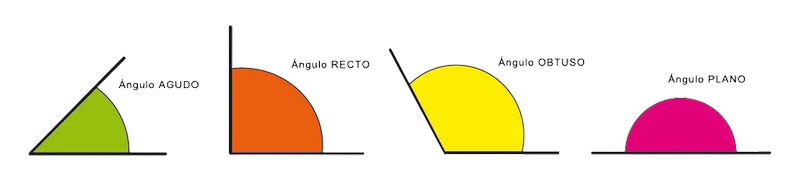
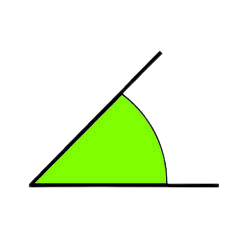
Un ángulo é o espazo comprendido entre dúas semirrectas co mesmo punto de orixe. Poden ser rectos, agudos, obtusos ou planos segundo a súa medida.
-
Exemplo:
-
Os ángulos mídense en grados sexaxesimais.
Bisectriz de un ángulo

-
Definición:
-
A bisectriz é a semirrecta, con orixe no vértice do ángulo, que o divide en dúas partes iguais.
-
Exemplo:
-
Ana trazou unha bisectriz no ángulo recto.
Cartabón

-
Definición:
-
O cartabón é un instrumento de debuxo técnico en forma de triángulo escaleno, cun ángulo recto, un de 60 e outro de 30 grados.
-
Exemplo:
-
Trouxeron todo o material menos o cartabón.
Compás

-
Definición:
-
O compás é un instrumento de precisión empregado para facer liñas curvas e círculos.
-
Exemplo:
-
Toda a clase estaba a debuxar círculos co compás.
Escuadro

-
Definición:
-
O escuadro, igual que o cartabón, serve para deseñar os trazados xeométricos. É un instrumento en forma de triángulo isóscele, cun ángulo recto e dous de 45 grados.
-
Exemplo:
-
Breixo tiña o escuadro e o cartabón gardados na mochila.
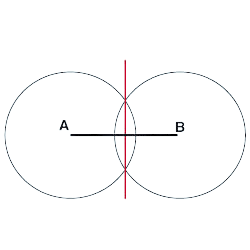
Mediatriz
-
Definición:
-
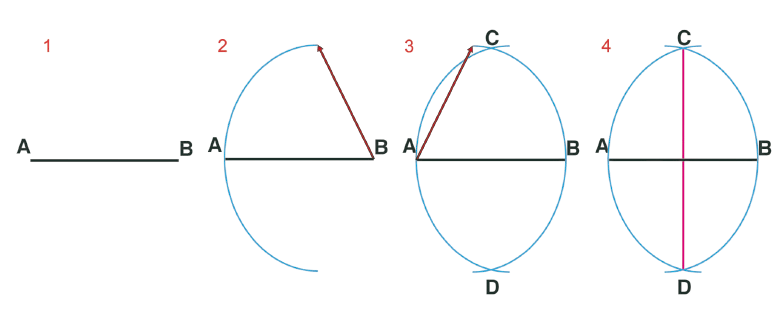
A mediatriz é unha semirrecta perpendicular ao punto medio dun segmento.
-
Exemplo:
-
A mediatriz divide o segmento que corta en dúas partes iguais.
Punto

-
Definición:
-
O punto é o lugar onde se cruzan dúas rectas. Non ten dimensión. Noméanse con letras maiúsculas (A, B, C...).
-
Exemplo:
-
Tiña todo o papel cheo de puntos
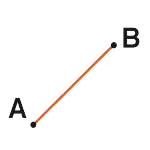
Recta
-
Definición:
-
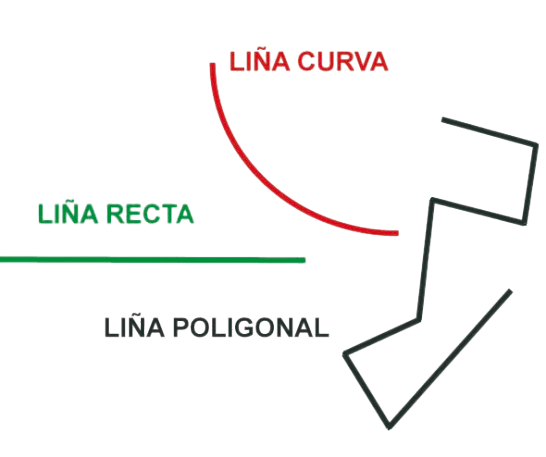
Sucesión de puntos, sen cambio de dirección, que non ten principio nin final. Unha recta xorde do corte entre dous planos.
-
Exemplo:
-
Trazar rectas coas regras é doado.
Rectas paralelas

-
Definición:
-
Son aquelas rectas que non se cruzan e manteñen sempre a mesma distancia entre si. Están no mesmo plano pero non teñen puntos en común.
-
Exemplo:
-
Os carrís das vías do tren son paralelos entre si.
Rectas perpendiculares

-
Definición:
-
Son aquelas rectas que se cruzan nun punto, mais sempre formando catro ángulos rectos.
-
Exemplo:
-
A rúa onde vives é perpendicular á rúa Areal.
 O debuxo técnico é unha forma gráfica de representar a realidade dun xeito claro e preciso.
O debuxo técnico é unha forma gráfica de representar a realidade dun xeito claro e preciso.