El responsable del mantenimiento del pazo observa que uno de los "tornarratos" cilíndrico del hórreo está dañado. Para poder arreglarlo habla con el cantero de la zona para que le fabrique una piedra similar.
El cantero le pide que le envíe el diámetro de la base de la piedra, pero el de mantenimiento, al ir a medirlo se da cuenta que no sabe con exactitud si la esquina del hórreo está colocada sobre el centro de la base del "tornarratos."
Utilizando una cinta métrica:
1) ¿Cómo puede asegurarse de que el ángulo que se ve en la foto es un ángulo central? ¿Cómo puede calcular el diámetro?
Pista 1
Hay varias formas de asegurarse. Te damos esta pista para ayudarte a redactar la solución, recuerda la fórmula:
\(L=\pi\cdot D\) o también, \(L=\pi\cdot2\cdot r\)
Una vez conseguido este reto, el cantero pide al de mantenimiento que le indique la superficie circular de la base de la piedra sobre la que reposa el hórreo.
2) ¿Sabes cómo puede hacer ese cálculo?
Pista 2
 |
El sector circular ocupa una parte del círculo.
En el caso del hórreo se ve fácilmente que fracción del círculo es la cuarta parte.
Si queremos saberlo con exactitud hay que comparar la amplitud del ángulo (o de su arco) con el total del círculo.
|
En este hórreo también está roto uno de los "tornarratos".
3) Haz un dibujo de la base circular en tu cuaderno y explica cómo podríamos hallar la superficie de la parte rota del círculo.
Pista 3
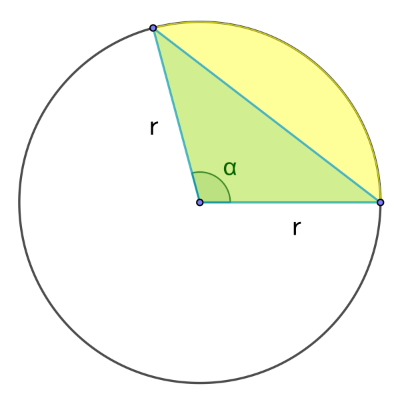
El sector circular contiene en su interior un triángulo isósceles cuyos lados son los radios de la circunferencia.
Utilizando este triángulo puedes hallar el área de un segmento circular.



 Para resolver el problema os damos varias pistas:
Para resolver el problema os damos varias pistas:
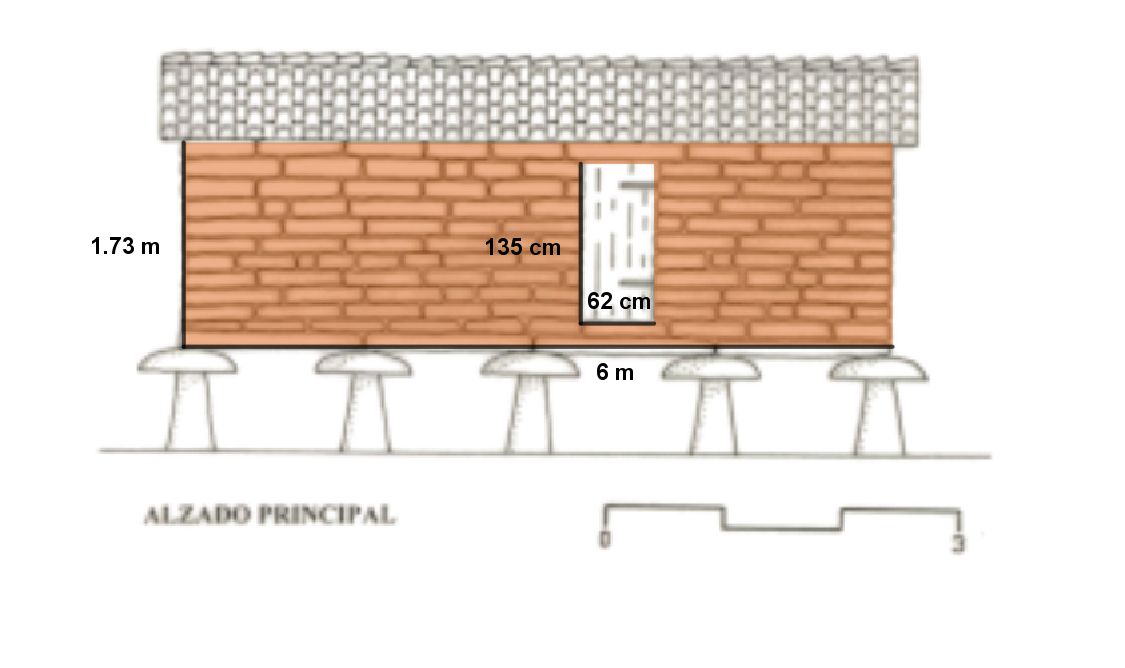
 La forma de los "tornarratos" no es igual en toda Galicia.
La forma de los "tornarratos" no es igual en toda Galicia.