Saltar la navegación

2. Conectando piedras

 

Glosario

Almena

Pazo con almenas en el muro exterior

Definición:

Cada uno de los prismas que se colocan en los muros de las antiguas fortalezas para defenderse.

Ejemplo:

En el Pazo de Vilastrille el muro de la entrada principal está coronado por almenas.

Bastión

Definición:

Parte de una fortaleza que se proyecta hacia el exterior. También se llama baluarte.

Ejemplo:

En los muros de las fortalezas puede verse este saliente.

Blasón

Panel con escudo de una Casa Blasonada en Viana do Bolo

Definición:

Escudo o los elementos que figuran en él. Cada una de sus divisiones se llaman cuarteles.

Ejemplo:

En la foto, panel de una Casa Blasonada en Viana do Bolo.

Linaje

Familia

Definición:

Ascendencia o descendencia de una familia.

Ejemplo:

Padres y madres son parte de tu linaje.

Pendón

Banderín con forma triangular

Definición:

Tipo de bandera utilizada como insignia desde la edad media, habitualmente más larga que ancha.

Ejemplo:

En las ferias medievales se cuelgan banderines con forma de pendón adornando las calles.

Conecta tu memoria

Personajes colocando piedras en una calzada romana

Para crear un panel descriptivo sobre un monumento antes tienes que aprender a ver lo que hay tras las piedras: historia, matemáticas, belleza... Aquí comienza tu investigación.

Uniendo piedras hacemos carreteras, uniendo plantas haremos jardines, y uniendo puntos formaremos figuras.

Te proponemos un recorrido a través del tiempo para conectar esos puntos en tu memoria.

Piedra a piedra

De la misma forma que un pazo se construye agrupando piedra a piedra, la geometría se va a construir punto a punto.

El punto, como la piedra de una fachada, es el elemento más simple que tenemos en geometría, no tiene longitud ni anchura, por lo que decimos que tiene dimensión cero. Sin embargo, agrupando puntos construimos otros elementos en el plano que nos permitirán hacer construcciones más complejas.

En este apartado introduciremos los conocimientos previos antes de realizar las actividades que nos permitirán elaborar nuestro panel.

Para ello trabajaremos con una plantilla que puede simbolizar la fachada o la planta de cualquier pazo o construcción.

Trama de puntos con la silueta del pazo / castillo

Conectando puntos

Conectando puntos

Si dibujamos varios puntos en un plano y los unimos se forman figuras. Conocerlas nos ayuda a construir edificios y también a describirlos.

Uniendo dos puntos formamos un segmento, prolongando por un extremo “infinitamente” semirrectas y prolongando por ambos puntos formamos rectas. Estos dos conceptos son abstractos ya que en la vida real no podemos hacer dibujos infinitos.

Si la recta es "infinita", estará formada por infinitos puntos, pero ¿sabrías decir cuántos son necesarios para determinarla de forma única?

¿Planta o alzado?

Usa la plantilla de puntos para determinar la forma del pazo y responde:

Trama de puntos con la silueta del pazo

  1. ¿Cuál es el número mínimo de segmentos que necesitas para formar la silueta?
  2. ¿Cuál puede ser la forma de sus torres?
  3. ¿Te parece la planta o el alzado?
  4. Si quisieras abrir una puerta, ¿qué cambios harías en el dibujo?
  5. Responde a la pregunta 1 con los cambios de la puerta.

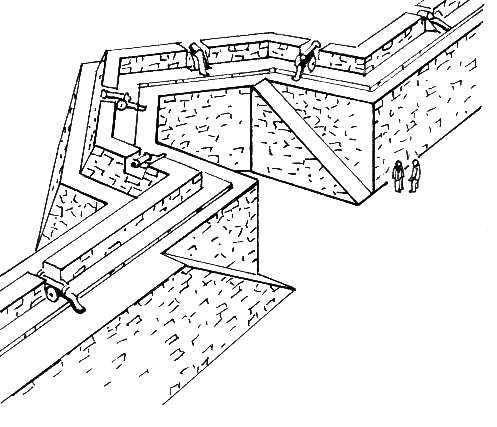
Vigilancia desde la torre

En las murallas con torres el ángulo de visión durante la vigilancia era vital. Su forma era determinante para que no quedasen flancos sin protección o para aminorar el daño de flechas y balas. ¿Era mejor que sus muros formasen un ángulo recto o un ángulo agudo?

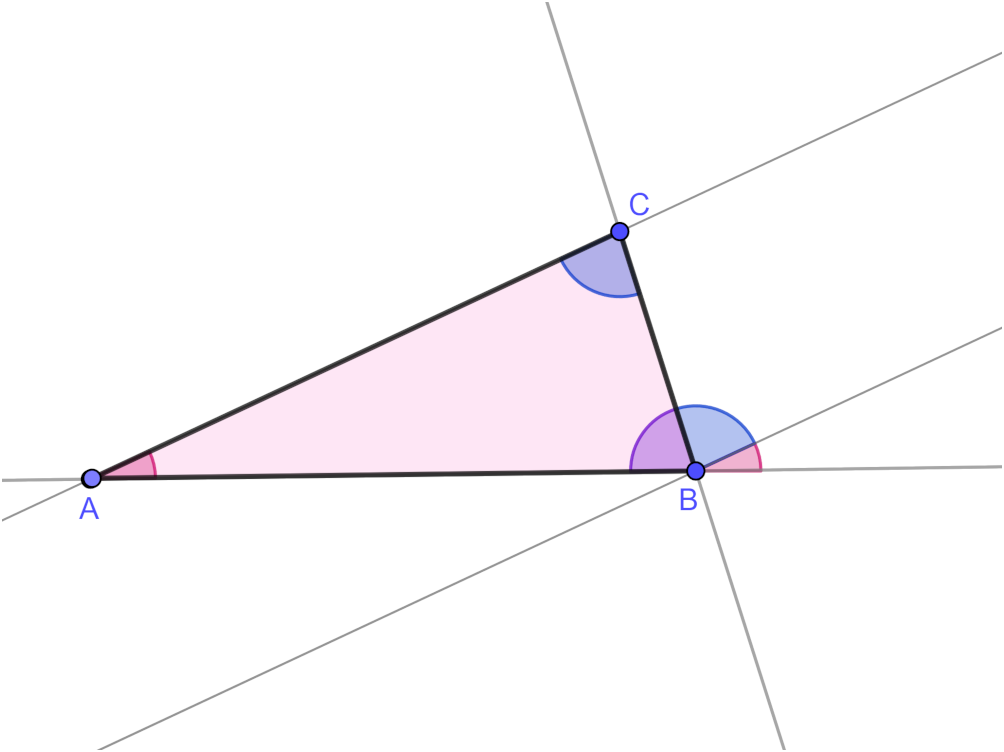
Para responder a estas preguntas recuerda este concepto: la figura comprendida entre dos rectas secantes se llama ángulo.

El concepto de ángulo está vinculado a las posiciones de dos rectas en el plano:

  • Si dos rectas se cortan formando un ángulo de 90º decimos que son perpendiculares.
  • En el plano, dos rectas que no se cortan se llaman paralelas.

Si no recuerdas los tipos de ángulos y sus posiciones usa el applet de repaso de GeoGebra que está más abajo para recordarlos.

Los ángulos de la torre del pazo

  • Una vez marcado el contorno del pazo, localiza sobre la plantilla los ángulos y clasifícalos.
  • Imagina un vigilante que haga guardia en el muro que está entre las dos torres. ¿Podría ver todas las paredes de las torres?
  • Investiga posibles zonas sin ángulo de visión en el applet de GeoGebra.
  • Curiosidad: la zona de un coche que queda sin visión desde los espejos se llama ángulo muerto, ¿a qué crees que se debe este nombre?

Hecho con GeoGebra®

Parte de recta comprendida entre dos puntos. Su longitud se llama distancia entre dos puntos.

Figura que forman dos rectas secantes. El punto donde se cortan se llama vértice.

Solo hay dos posiciones de rectas en el plano: o se cortan o no se cortan.

Al vigilar desde las murallas, las paredes de la torre podían dejar zonas en las que no se veía a las personas atacantes (ángulo muerto).

Recuerda que hay ángulos cóncavos y convexos.

Conectando segmentos

El triángulo mola

Taller de ilustración en la Feria Medieval de Monforte de Lemos

Pensemos ahora que ocurre si conectamos tres segmentos de forma consecutiva y el tercero se une con el primero.

Con tres segmentos unidos de esta forma tenemos un polígono denominado triángulo. Cada uno de los segmentos que lo forman se llama lado. Dependiendo de la medida de sus lados y de la de sus ángulos daremos nombre a distintos tipos de triángulos.

En la imagen el artesano forma un triángulo a partir de un cordón con 12 nudos. Los lados tienen 3, 4 y 5 nudos.

  • ¿Qué tipo de triángulo es?
  • ¿Conoces la relación entre sus lados?

En el bloque 3 se tratarán de forma específica este tipo de triángulos, ahora repasamos las dos clasificaciones:

- Según sus lados: equilátero, isósceles, y escaleno.

- Según sus ángulos: acutángulo, rectángulo y obtusángulo.

¿Conoces alguna torre que tenga solo tres paredes? No es fácil encontrarla y sin embargo esta figura es la base de muchas construcciones.

La torre de las tres esquinas

La torre de las tres esquinas o de La Mola

La base triangular es la que implica menos paredes en una construcción.

1) ¿Cómo se dibuja la planta de esta torre?

2) Clasifica esa figura.

Las torres con base poligonal son prismas y se describen por el polígono de la base. A este dato se le añade la altura.

La Torre de la Mola es un prisma de base triangular con 17 metros de altura.

Conectando ángulos

Observa la imagen adjunta y usa las posiciones relativas de los ángulos para indicar cuál es la suma de dichos ángulos. Escribe las propiedades que has usado.

Suma ángulos de triángulo

Solución

La suma de los ángulos de un triángulo es siempre 180º.

Hecho con GeoGebra®

¿Y si no lo veo?

Desplaza los puntos rojos y comprueba que en todos los casos la suma de los ángulos del triángulo es 180º.

Hecho con GeoGebra®

Tiene sus tres lados iguales.

Solo dos lados con la misma medida.

Los tres lados miden diferente.

Los tres ángulos son agudos, menores que 90º.

Tiene un ángulo recto.

Tiene un ángulo obtuso, mayor que 90º.

Es la Torre de la Mola.

Es la Torre de la Mola, en Alicante.

Repasa ángulos y sus posiciones

Utiliza esta interactividad para aprender los diferentes tipos de ángulos que podemos encontrar y sus posiciones relativas. Arrastra los puntos para cambiar sus aberturas.

https://www.geogebra.org/m/kzkdmcng (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/kzkdmcng,Tipos%20de%20%E1ngulos%20y%20posiciones%20relativas%20relativas,0,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Autoría: Javier Cayetano Rodríguez

Definiciones

Científica con rosco

Repasa rectas

Punto

Menor objeto del espacio. Un punto no tiene dimensión.

Recta

Línea más corta que une dos puntos. La longitud de una recta es infinita.

Rectas paralelas

Dos rectas son paralelas cuando no tienen ningún punto en común.

Rectas secantes

Dos rectas son secantes cuando se cortan en un punto.

Segmento

Parte de recta comprendida entre dos puntos. Su longitud se llama distancia entre dos puntos.

Mediatriz de un segmento

Recta perpendicular al segmento que pasa por su punto medio. Lo divide en dos partes iguales.

Repasa ángulos

Ángulo

Figura que forman dos rectas secantes. El punto donde se cortan se llama vértice.

Grado sexagesimal

Unidad de medida de ángulos.

Si colocamos el ángulo con su vértice en el centro de un círculo, este nos permite medir su amplitud.

Dividiendo el círculo en trescientas sesenta partes, cada una de ellas tendrá de amplitud un grado sexagesimal.

El sentido de medición es el contrario al giro de las agujas del reloj.

Bisectriz de un ángulo

Recta que divide a un ángulo en dos partes iguales.

Repasa figuras

Triángulo

Figura plana cerrada formada por tres segmentos.

Cuadrilátero

Figura plana cerrada formada por cuatro segmentos.

Polígono

Figura plana cerrada formada por varios segmentos. Generaliza a las dos definiciones anteriores.

Diagonal

Segmento que une dos vértices no consecutivos.

Circunferencia

Figura plana cerrada y curva cuyos puntos están todos a la misma distancia de un punto llamado centro.

La superficie que encierra se llama círculo.

Perímetro

Longitud del contorno de una figura.

Área

Medida de la superficie de una figura.

Lista de cotejo de ángulos y triángulos

Completa la lista de cotejo marcando las casillas al realizar las actividades correspondientes.

%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%E6%F7%F8%FD%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A6%A6%A6%A6%A7%A6%AA%BF%A3%A0%A2%B0%BE%B0%E6%FB%E6%FE%F7%B0%A8%B0%A0%BC%A2%B2%D1%FD%FC%F7%F1%E6%F3%FC%F6%FD%B2%E2%FB%F7%F6%E0%F3%E1%B0%BE%B0%E1%E7%F0%E6%FB%E6%FE%F7%B0%A8%B0%D1%FD%FF%E2%E0%E7%F7%F0%F3%B2%FE%F3%E1%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%F7%E1%B2%E0%F7%F3%FE%FB%E8%F3%F6%F3%E1%B2%EB%B2%FE%FD%E1%B2%F1%FD%FC%E6%F7%FC%FB%F6%FD%E1%B2%E0%F7%E2%F3%E1%F3%F6%FD%E1%B0%BE%B0%FE%F7%E4%F7%FE%E1%B0%A8%C9%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A1%CE%B0%B2%F4%F3%F1%F7%AF%CE%B0%D3%E6%F9%FB%FC%E1%FD%FC%B2%DA%EB%E2%F7%E0%FE%F7%F5%FB%F0%FE%F7%CE%B0%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A2%A2%A2%A2%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%D5%FE%FD%E1%F3%E0%FB%FD%B2%F1%FD%FC%E1%E7%FE%E6%F3%F6%FD%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%F4%FD%FC%E6%AC%AE%F0%E0%AC%CE%FC%AE%E2%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%F3%FE%FB%F5%FC%AF%CE%B0%F8%E7%E1%E6%FB%F4%EB%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%F1%FF%CE%B0%AC%AE%BD%E2%AC%CE%FC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%CE%FC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%D1%FD%FC%F7%F1%E6%F3%FC%F6%FD%B2%E2%E7%FC%E6%FD%E1%A8%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%CE%FC%AE%BD%FA%A0%AC%CE%FC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F7%FE%B2%F1%FD%FC%F1%F7%E2%E6%FD%B2%F6%F7%B2%E1%F7%F5%FF%F7%FC%E6%FD%BE%B2%E0%F7%F1%E6%F3%B2%EB%B2%E1%F7%FF%FB%E0%E0%F7%F1%E6%F3%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F7%FE%B2%F1%FD%FC%F1%F7%E2%E6%FD%B2%F6%F7%B2s%FC%F5%E7%FE%FD%B2%EB%B2%E1%E7%B2%E0%F7%FE%F3%F1%FBa%FC%B2%F1%FD%FC%B2%FE%F3%E1%B2%E2%FD%E1%FB%F1%FB%FD%FC%F7%E1%B2%F6%F7%B2%F6%FD%E1%B2%E0%F7%F1%E6%F3%E1%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F7%FE%B2%F1%FD%FC%F1%F7%E2%E6%FD%B2%F6%F7%B2s%FC%F5%E7%FE%FD%B2%FF%E7%F7%E0%E6%FD%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%D1%FD%FC%F7%F1%E6%F3%FC%F6%FD%B2%E1%F7%F5%FF%F7%FC%E6%FD%E1%A8%B2%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FC%FD%E8%F1%FD%B2%FE%FD%E1%B2%E6%FB%E2%FD%E1%B2%F6%F7%B2%E6%E0%FBs%FC%F5%E7%FE%FD%E1%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%C2%E7%F7%F6%FD%B2%F6%F7%E1%F1%E0%FB%F0%FB%E0%B2%E7%FC%F3%B2%E6%FD%E0%E0%F7%B2%F3%B2%E2%F3%E0%E6%FB%E0%B2%F6%F7%B2%E1%E7%B2%F0%F3%E1%F7%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F7%FE%B2%E4%F3%FE%FD%E0%B2%F6%F7%B2%FE%F3%B2%E1%E7%FF%F3%B2%F6%F7%B2%FE%FD%E1%B2s%FC%F5%E7%FE%FD%E1%B2%FB%FC%E6%F7%E0%FB%FD%E0%F7%E1%B2%F6%F7%B2%E7%FC%B2%E6%E0%FBs%FC%F5%E7%FE%FD%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%C6%FB%E2%FD%E1%B2%F6%F7%B2s%FC%F5%E7%FE%FD%E1%B2%EB%B2%E2%FD%E1%FB%F1%FB%FD%FC%F7%E1%A8%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%BD%FA%A0%AC%CE%FC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DA%F7%B2%E0%F7%E2%F3%E1%F3%F6%FD%B2%FE%FD%E1%B2%E6%FB%E2%FD%E1%B2%F6%F7%B2s%FC%F5%E7%FE%FD%E1%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DA%F7%B2%E0%F7%E2%F3%E1%F3%F6%FD%B2%FE%F3%E1%B2%E2%FD%E1%FB%F1%FB%FD%FC%F7%E1%B2%F6%F7%B2%FE%FD%E1%B2s%FC%F5%E7%FE%FD%E1%BC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A1%CE%B0%B2%F4%F3%F1%F7%AF%CE%B0%D3%E6%F9%FB%FC%E1%FD%FC%B2%DA%EB%E2%F7%E0%FE%F7%F5%FB%F0%FE%F7%CE%B0%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A2%A2%A2%A2%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%D6%F7%F4%FB%FC%FB%F1%FB%FD%FC%F7%E1%B2%E0%F7%E4%FB%E1%F3%F6%F3%E1%BC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%F4%FD%FC%E6%AC%AE%F0%E0%AC%CE%FC%AE%E2%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%F3%FE%FB%F5%FC%AF%CE%B0%F8%E7%E1%E6%FB%F4%EB%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%F1%FF%CE%B0%AC%CE%FC%AE%BD%E2%AC%CE%FC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%CF%BE%B0%FA%F3%E1%DE%FD%F5%FD%B0%A8%F4%F3%FE%E1%F7%BE%B0%E7%E0%FE%DE%FD%F5%FD%B0%A8%B0%B0%BE%B0%FA%F3%E1%D1%FD%FF%FF%E7%FC%FB%E6%EB%B0%A8%E6%E0%E7%F7%BE%B0%E7%E0%FE%D1%FD%FF%FF%E7%FC%FB%E6%EB%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%DE%DD%D5%DD%CD%D1%C0%D7%D3%D5%D3%DE%BC%A3%BC%E2%FC%F5%B0%BE%B0%FA%F3%E1%D6%F7%F1%FD%E0%F3%E6%FB%E4%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%E7%E0%FE%D6%F7%F1%FD%E0%F3%E6%FB%E4%F7%B0%A8%B0%B0%BE%B0%E1%F3%E4%F7%D6%F3%E6%F3%B0%A8%E6%E0%E7%F7%BE%B0%E7%E1%F7%E0%D6%F3%E6%F3%B0%A8%E6%E0%E7%F7%BE%B0%F4%FD%FD%E6%F7%E0%B0%A8%B0%D7%E1%E6%F3%B2%AE%F3%B2%FA%E0%F7%F4%AF%FA%E6%E6%E2%E1%A8%BD%BD%F7%E1%BC%E5%FB%F9%FB%E2%F7%F6%FB%F3%BC%FD%E0%F5%BD%E5%FB%F9%FB%BD%DE%FB%E1%E6%F3%CD%F6%F7%CD%F1%FD%FF%E2%E0%FD%F0%F3%F1%FB%B7%D1%A1%B7%D0%A1%FC%AC%FE%FB%E1%E6%F3%B2%F6%F7%B2%F1%FD%E6%F7%F8%FD%AE%BD%F3%AC%B2%E1%F7%B2%F7%FC%F1%E7%F7%FC%E6%E0%F3%B2%F0%F3%F8%FD%B2%E7%FC%F3%B2%FE%FB%F1%F7%FC%F1%FB%F3%AE%BD%F0%E0%AC%AE%F3%B2%FA%E0%F7%F4%AF%FA%E6%E6%E2%E1%A8%BD%BD%F1%E0%F7%F3%E6%FB%E4%F7%F1%FD%FF%FF%FD%FC%E1%BC%FD%E0%F5%BD%FE%FB%F1%F7%FC%E1%F7%E1%BD%F0%EB%BF%FC%F1%BF%E1%F3%BD%A6%BC%A2%BD%F6%F7%F7%F6%BC%F5%FE%AC%D1%E0%F7%F3%E6%FB%E4%F7%B2%D1%FD%FF%FF%FD%FC%E1%B2%C0%F7%F1%FD%FC%FD%F1%FB%FF%FB%F7%FC%E6%FD%B2%DC%FD%B2%F1%FD%FF%F7%E0%F1%FB%F3%FE%BF%D1%FD%FF%E2%F3%E0%E6%FB%E0%B2%FB%F5%E7%F3%FE%B2%A6%BC%A2%B2%AE%BD%F3%AC%B0%BE%B0%E7%E1%F7%C1%F1%FD%E0%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%D1%FD%FF%E2%FE%FB%E6%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B0%BE%B0%FF%E1%F5%D6%FD%FC%F7%B0%A8%B0%DA%F7%F1%FA%FD%B0%BE%B0%FF%E1%F5%DB%FC%C2%E0%FD%F5%E0%F7%E1%E1%B0%A8%B0%D7%FC%B2%E2%E0%FD%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C7%FC%E0%F7%F3%FE%FB%E8%F7%F6%B0%A8%B0%C1%FB%FC%B2%F1%FD%FF%E2%FE%F7%E6%F3%E0%B0%BE%B0%FF%E1%F5%E6%F3%E1%F9%DC%E7%FF%F0%F7%E0%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E6%F3%E0%F7%F3%E1%B0%BE%B0%FF%E1%F5%DC%F3%FF%F7%B0%A8%B0%DC%FD%FF%F0%E0%F7%B0%BE%B0%FF%E1%F5%D6%F3%E6%F7%B0%A8%B0%D4%F7%F1%FA%F3%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%B0%A8%B0%D6%F7%E1%F1%F3%E0%F5%F3%E0%B0%BE%B0%FF%E1%F5%DE%FB%E1%E6%B0%A8%B0%FE%FB%E1%E6%F3%CD%F6%F7%CD%F1%FD%E6%F7%F8%FD%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%E1%B0%A8%B0%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%B0%A8%B0%E2%E7%FC%E6%FD%B0%BE%B0%FF%E1%F5%C0%F7%F0%FD%FD%E6%B0%A8%B0%C0%F7%FB%FC%FB%F1%FB%F3%E0%B0%BE%B0%FF%E1%F5%D6%F7%FE%F7%E6%F7%B0%A8%B0-%C1%F7%F5%E7%E0%FD%B2%E3%E7%F7%B2%F6%F7%E1%F7%F3%B2%F0%FD%E0%E0%F3%E0%B2%E6%FD%F6%FD%E1%B2%FE%FD%E1%B2%F1%F3%FF%E2%FD%E1%B2%F6%F7%FE%B2%F4%FD%E0%FF%E7%FE%F3%E0%FB%FD%AD%B0%EF%EF
Navegador incompatible

Cuando hayas completado esta lista podrás pasar al apartado siguiente.

Community

Creado con eXeLearning (Ventana nueva)