3.1 Porcentaxes
Na nosa vida atopámonos moitas veces en situacións en que oímos que "tal artigo ten unha rebaixa do 20 por cento" ou que "o IVE aplicado á factura do recibo da luz é do 18 por cento". Ambas as expresións definen a porcentaxe, é dicir, o número de partes referidas das cen iguais en que se pode dividir unha cantidade. No noso caso, o prezo do artigo ou o seu importe, que constitúe a rebaixa ofertada ou o sobrecusto que teremos que pagar por causa do IVE.
Matematicamente falando, unha porcentaxe pódese concibir como unha proporción, como unha razón cuxo consecuente é 100 ou como un número decimal.
Unha porcentaxe indica unha proporción
Cando dicimos que o 40 % da xuventude se comunica a través das redes sociais, estamos a dicir que de cada 100 rapaces utilizan as redes sociais para comunicarse entre eles uns 40. Podemos representar estes datos nunha táboa.
|
Total |
100 |
200 |
300 |
50 |
25 |
350 |
··· |
|
Parte (40%) |
40 |
80 |
120 |
20 |
10 |
? |
··· |
Se observamos a táboa vemos que se trata dunha proporcionalidade directa, o que nos permite tratar unha situación de porcentaxe como unha situación de proporcionalidade.
Daquela, se un 40 % da xuventude usa as redes sociais para comunicarse, de 350 rapaces, cantos as usarán?
 |
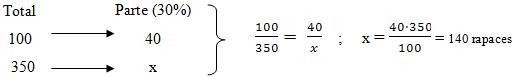Ao utilizar as proporcións, o verdadeiramente importante é gardar a orde nas razóns. Por exemplo, se na primeira razón puxemos 
, na seguinte razón debemos pór tamén .
|
Para calcular un determinado tanto por cento dunha cantidade,multiplícase o tanto pola cantidade e o resultado divídese entre 100
|
t % de C = |
Unha porcentaxe é unha fracción
Coller o 40 % dunha cantidade é o mesmo que dividir a citada cantidade en 100 partes e tomar 40, é dicir, tomar a fracción .
Daquela, no exemplo anterior:
40 % de 350 = 
de 350 = 
= 140.
|
Unha porcentaxe pódese calcular como a fracción dunha cantidade
|
t % de C = |
de C =
Unha porcentaxe asóciase a un número decimal
Unha porcentaxe pódese expresar como unha fracción, como vimos no apartado anterior. Á súa vez, unha fracción pódese expresar en forma de número decimal, o que nos vai permitir utilizar un xeito rápido para o cálculo de porcentaxes.
40 % en forma de fracción é , e á súa vez, en forma decimal, 40 : 100 = 0,40
Xa que logo, o 40 % de 350 = 0,40 · 350 = 140
Para calcularmos unha porcentaxe utilizando o número decimal que representa o que facemos é:
multiplicar o tanto por cento expresado en forma decimal pola cantidade total.
Introduce o numerador e o denominador da fracción e observa as representacións como rectángulo e como sector.
Compartida por jminfante1 - LicenzaCC-BY-SA, GeoGebra Terms of Use
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0