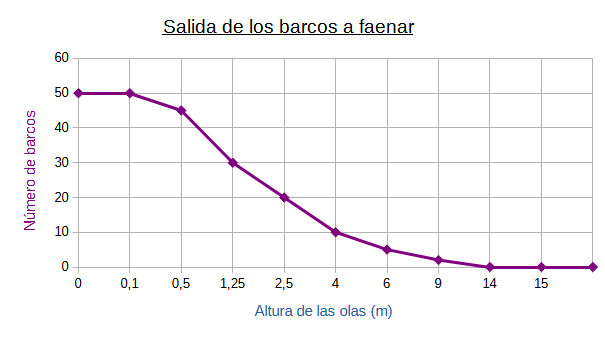
Relaciones dadas por las tablas
Otra forma muy útil de representar funciones es a través de una tabla de valores.
Una tabla de valores no es más que una tabla donde indicamos los valores de la variable independiente y su valor correspondiente de la variable dependiente.
Estas tablas son muy útiles ya que nos permiten visualizar los pares de puntos que luego representaremos en una gráfica. Veamos unos ejemplos.
Ejemplos
El precio del pescado
Volvamos a la gráfica "Precio del pescado" que vimos en el apartado "Funciones en forma de gráfica"
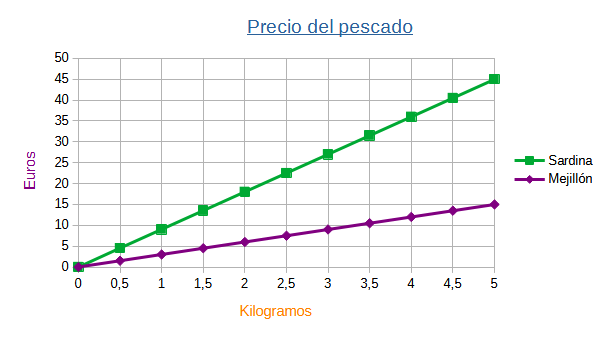
Podemos recoger de esta tabla las parejas de puntos que se corresponden con cada una de las funciones y escribirlos en una tabla.
Tabla vertical
En esta gráfica, tenemos dos funciones, así que tendremos dos tablas: una para el precio de la sardina, y otra para el precio del mejillón.
Veamos cómo sería la tabla vertical para la función que relaciona los kilos de sardina con su precio:
| x (Kg) | y (€) |
|---|---|
| 0 | 0 |
| 0,5 | 4,5 |
| 1 | 9 |
| 1,5 | 13,5 |
| 2 | 18 |
| 2,5 | 22,5 |
| 3 | 27 |
| 3,5 | 31,5 |
| 4 | 36 |
| 4,5 | 40,5 |
| 5 | 45 |
| x (Kg) | y (€) |
|---|---|
| 0 | 0 |
| 0,5 | 1,5 |
| 1 | 3 |
| 1,5 | 4,5 |
| 2 | 6 |
| 2,5 | 7,5 |
| 3 | 9 |
| 3,5 | 10,5 |
| 4 | 12 |
| 4,5 | 13,5 |
| 5 | 15 |
Tabla horizontal
También podemos escribir la tabla en horizontal. Veamos en este caso las tablas escritas en horizontal:
| x (Kg) | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| y (€) | 0 | 4,5 | 9 | 13.5 | 18 | 22,5 | 27 | 31,5 | 36 | 40,5 | 45 |
| x (Kg) | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| y (€) | 0 | 1,5 | 3 | 4.5 | 6 | 7,5 | 9 | 10,5 | 12 | 13,5 | 15 |
Haciendo una tarta
Otra utilidad de las tablas de datos es poder hacer la operación inversa, es decir, dibujar la gráfica a partir de los datos obtenidos experimentalmente o a través de una expresión matemática. Veamos cómo se hace una gráfica a partir de los datos de una tabla.
¡En casa de Mariña hoy están de fiesta! Así que, a Mariña le toca preparar la tarta, su madre le da la cantidad de harina que necesita para hacer la tarta en función de las personas a las que va a invitar, así:
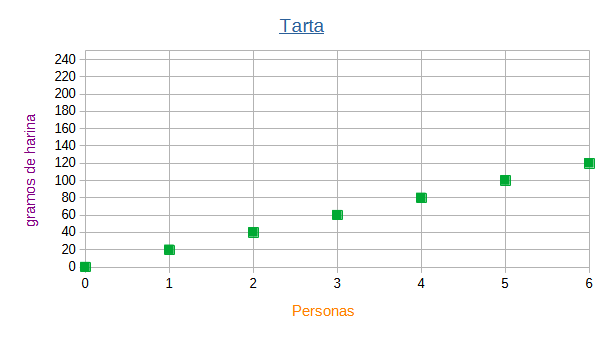
| Número de personas | Gramos de harina |
|---|---|
| 0 | 0 |
| 1 | 40 |
| 2 | 80 |
| 3 | 120 |
| 4 | 160 |
| 5 | 200 |
| 6 | 220 |
Como podéis observar, en este gráfico no tiene sentido unir los puntos, ya que no puedes dar de comer a media persona o a una persona y media. Es importantísimo ver en contexto en el se trabaja, es decir, cuál es la variable dependiente y cuál la independiente para saber si tiene sentido unir los puntos o no
