Glosario
Algoritmo
-
Definición:
-
Conjunto de instrucciones ordenadas que sirven para explicar los pasos de una tarea o resolver un ejercicio.
-
Ejemplo:
-
Las instrucciones que se dan a los ordenadores para hacer una tarea son algoritmos.
Fisgando en N
3.9. Guíame
Faros
Los faros han sido herramientas esenciales para la navegación marítima a lo largo de la historia.
Situados en las costas, los faros emiten destellos de luz a intervalos regulares, ayudando a los barcos a orientarse y evitando que se acerquen peligrosamente a la costa o a zonas de rocas.
Estos destellos no solo guían a los marineros durante la noche y en condiciones de baja visibilidad, sino que también sirven como puntos de referencia, asegurando una navegación segura.
Alumbrando la costa
Los faros de la Costa de la Vela y los faros de las islas Cíes y de las islas Ons iluminan la entrada a las Rías de Pontevedra y de Vigo.
El faro de Punta Robaleira emite un destello cada 8 segundos, el faro de Punta Couso cada 10 segundos, el faro de Cíes cada 20 segundos y el faro de Ons cada 24 segundos.
Un barco acaba de ver las luces de los faros de Punta Robaleira, Punta Couso, Cíes y Ons al mismo tiempo, ¿cuánto tiempo pasará hasta que las luces de los cuatro faros vuelvan a coincidir?
https://www.geogebra.org/m/m5y28yby (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Solución alumbrando la costa
https://www.geogebra.org/m/mtaaucy4 (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Opción 1
Calculamos los múltiplos de los destellos de cada faro y detectamos cuándo coinciden los cuatro por primera vez.
| Faro | Período de la luz | Tiempos en los que hay destellos de luz |
|---|---|---|
| Faro de Punta Robaleira | 8 segundos | 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, ... |
| Faro de Punta Couso | 10 segundos | 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120 ... |
| Faro de Cíes | 20 segundos | 20, 30, 40, 60, 80, 100,120 ,... |
| Faro de Ons | 24 segundos | 24, 48, 72, 96,120, ... |
El primer múltiplo común de los cuatro faros es 120.
Coinciden cada 120 s, o lo que es lo mismo, cada 2 minutos.
Opción 2
Podemos utilizar otras estrategias similares a la anterior pero agrupando números. Veamos cómo se realizaría agrupando números de dos en dos.
| Faro de Punta Robaleira | 8 | 8, 16, 24, 32, 40, 48, ..., 120, ... |
| Faro de Ons | 24 | 24, 48, ..., 120, ... |
| Faro de Punta Couso | 10 | 10, 20, 30, 40, ...,120, ... |
| Faro de Cíes | 20 | 20, 40, 60, ..., 120, ... |
Comparamos los dos resultados anteriores haciendo los múltiplos de 20 y de 24:
| 20 | 20, 40, 60, 80, 100, 120, ... |
| 24 | 24, 48, 72, 96, 120, ... |
Opción 3
Por último, veremos cómo se calcularía el múltiplo común más pequeño mediante la descomposición en factores primos.
8 = 2 · 2 · 2 = 23 segundos
10 = 2 · 5 segundos
20 = 2 · 2 · 5 = 22 · 5 segundos
24 = 2 · 2 · 2 · 3 = 23 · 3 segundos
Un múltiplo que contiene a los factores de los cuatro números es 23 · 5 · 3 = 8 · 5 · 3 = 120 segundos
Los cuatro faros coinciden cada 120 s, o lo que es lo mismo, cada 2 min.
El arte de calcular el mínimo común múltiplo
En el ejercicio anterior vimos que hay varias formas de calcular el mínimo común múltiplo.
Se trata de distintos "algoritmos", es decir, pasos para llegar al número buscado.
Vamos a revisar algunas formas de calcularlo.
Partiendo de la definición
La definición de mínimo común múltiplo de dos o más números indica que es el menor de todos sus múltiplos comunes.
Por tanto:
INICIO DEL ALGORITMO
- PASO 1: hacemos una lista con los múltiplos de cada número.
- PASO 2: buscamos la primera coincidencia entre los listados anteriores.
FIN DEL ALGORITMO
Cualquier otra coincidencia es un múltiplo, pero ya no sería el menor.
En el ejemplo anterior es la opción (1) de la solución.
Factorizando
Este algoritmo también se basa en que cualquier múltiplo común a dos o más números debe estar formado por todos los factores de cada uno de esos números.
INICIO DEL ALGORITMO
PASO 1: hallamos la factorización prima de cada uno de los números.
PASO 2: formamos el mcm eligiendo sólo los factores primos necesarios para que en el resultado estén ambos números.
FIN DEL ALGORITMO
Ejemplo: calcular el mcm (20, 8)
INICIO DEL ALGORITMO
PASO 1: factorización prima de cada número
- 20 = 10 · 2 = 5 · 2 · 2
- 8 = 4 · 2 = 2 · 2 · 2
PASO 2: elegimos los factores que forman el menor de los múltiplos de ambos, solo los necesarios para que el resultado contenga a ambos números.
Un múltiplo común podría ser el producto de todos ellos 5 · 2 · 2 · 2 · 2 · 2 = 160 pero, ¿es el menor?
Para garantizar que sea el menor de todos en ese producto, dejamos solamente los estrictamente necesarios para formar ambos números:
5 · 2 · 2 · 2 = 40
Observa que en el producto 5 · 2 · 2 · 2 están los factores del 20 (5, 2, 2) y también del 8 (2, 2, 2).
FIN DEL ALGORITMO
En el ejemplo anterior, este algoritmo se utiliza en la opción (3) de la solución.
Si expresamos los factores repetidos en forma de potencia, debemos prestar atención a los exponentes para garantizar que todos los factores que forman el 8 y el 20 están en esa expresión.
23 contiene a 22 por tanto están esos factores del 20.
mcm (20, 8) = 5 · 23
Y aún hay más
En el apartado 3.10. encontrarás aún más formas de calcular el mcm.
Es importante que las entiendas todas y que no confundas la definición con las distintas formas de calcularlo.
Encadena mcm
Tres cantidades
El cálculo del mcm de más de dos números se puede hacer por los métodos del apartado anterior, o bien agrupando de dos en dos y haciendo el mcm del resultado.
En el ejemplo anterior es la opción (2) de la solución.
Calcula el mcm (a, b, c)
INICIO DEL ALGORITMO
PASO 1: calculamos el mcm (a, b) = d
PASO 2: calculamos el mcm (b, c) = e
PASO 3: calculamos el mcm (d, e) = f
El resultado del mcm (a, b, c) es f.
FIN DEL ALGORITMO
Cuatro cantidades
En el ejercicio anterior hay 4 números. Se agrupan los dos primeros y los dos últimos.
Lo expresamos paso a paso:
Calcula el mcm (a, b, c, d)
INICIO DEL ALGORTIMO
PASO 1: mcm (a, b) = e
PASO 2: mcm (c, d) = f
PASO 3: mcm (e, f) = g
FIN DEL ALGORITMO
El resultado del mcm (a, b, c, d) es g.
Piensa:
¿Cómo harías el mcm de 5 números?
Mcm con calculadora
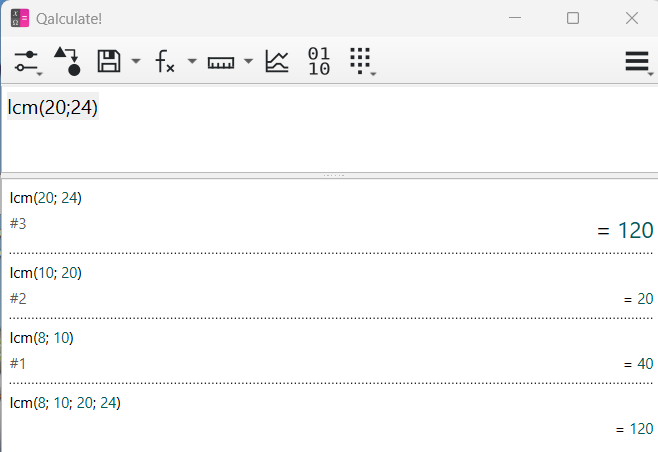
Las calculadoras actuales, tanto físicas como el software de ordenador, permiten calcular el mínimo común múltiplo.
Para ello debes mirar en el manual de instrucciones o en la ayuda cómo funciona.
En el ejemplo de la imagen utilizamos la calculadora Qalculate!, que de forma sencilla nos halla el mcm.
Las iniciales lcm se corresponden con la traducción en inglés de mínimo común múltiplo:
least common multiple.
Otro software que permite hallar el mcm es geogebra.
Los dos programas anteriores permiten calcular simultáneamente el mcm de más de dos cantidades, pero no siempre ocurre.
En ese caso puedes utilizar la propiedad que explicamos en el apartado anterior, calcular de dos en dos y luego el de sus resultados.
Alumbrando el paseo
El ayuntamiento de un pueblo pesquero ha decidido acondicionar el paseo marítimo para hacerlo más agradable para los habitantes y turistas. Han decidido instalar farolas y bancos a lo largo de todo el paseo para mejorar la iluminación y ofrecer lugares donde descansar y disfrutar de las vistas al mar.
Como parte del equipo encargado de este proyecto, te han asignado la tarea de determinar a qué distancia deben colocarse las farolas y los bancos para que coincidan en algunos puntos específicos del paseo. Esto no solo mejorará la estética del paseo, sino que también proporcionará áreas bien iluminadas y cómodas para los paseantes.
Actividad:
En un paseo marítimo con árboles cada 15 metros se quieren colocar farolas y bancos.
Al principio del paseo se instalará la primera farola y el primer banco junto a uno de los árboles.
Las siguientes farolas se colocarán cada 12 metros y los bancos cada 18 metros.
- ¿A qué distancia del inicio del paseo coincidirán por primera vez una farola y un banco?
- ¿Cuándo coincidirán por primera vez una farola, un banco y un árbol?
- Si el paseo marítimo mide 1800 metros, ¿cuántas veces coincidirán una farola, un banco y un árbol a lo largo del paseo?
Practica el mcm de dos números
Practica el cálculo del mínimo común múltiplo de dos números con este applet.
Cada respuesta correcta suma 2 puntos, y cada fallo resta 1 punto. La puntuación máxima es 10.
https://www.geogebra.org/m/f7djbnhj (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Lista de cotejo de algoritmos de cálculo del mcm
Completa la lista de cotejo marcando las casillas al realizar las actividades correspondientes.
%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%E6%F7%F8%FD%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A6%A6%A6%A6%A7%A6%AA%BF%A3%A0%A2%B0%BE%B0%E6%FB%E6%FE%F7%B0%A8%B0%A1%BC%AB%B2%D5%E7%7F%F3%FF%F7%B0%BE%B0%E1%E7%F0%E6%FB%E6%FE%F7%B0%A8%B0%D1%FD%FF%E2%E0%E7%F7%F0%F3%B2%E1%FB%B2%FA%F3%E1%B2%F7%FC%E6%F7%FC%F6%FB%F6%FD%B2%FE%F3%E1%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%F7%E1%B2%EB%B2%F1%FD%FC%E6%F7%FC%FB%F6%FD%E1%B2%F3%FC%E6%F7%E0%FB%FD%E0%F7%E1%B0%BE%B0%FE%F7%E4%F7%FE%E1%B0%A8%C9%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%AA%BC%A4%A4%A4%A5%E2%EA%A9%CE%B0%AC%D3%FE%E7%FF%F0%E0%F3%FC%F6%FD%B2%FE%F3%B2%F1%FD%E1%E6%F3%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DB%FC%E6%F7%E0%E2%E0%F7%E6%FD%B2%E7%FC%B2%F7%FC%E7%FC%F1%FB%F3%F6%FD%B2%F1%FD%FC%B2%F1%FD%FB%FC%F1%FB%F6%F7%FC%F1%FB%F3%E1%B2%F6%F7%B2%FFh%FE%E6%FB%E2%FE%FD%E1%B2%F6%F7%B2%FFs%E1%B2%F6%F7%B2%F6%FD%E1%B2%F1%F3%FC%E6%FB%F6%F3%F6%F7%E1%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%AA%BC%A4%A4%A4%A5%E2%EA%A9%CE%B0%AC%D7%FE%B2%F3%E0%E6%F7%B2%F6%F7%B2%F1%F3%FE%F1%E7%FE%F3%E0%B2%F7%FE%B2%FF%F1%FF%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F1a%FF%FD%B2%E1%F7%B2%F1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%FF%F1%FF%B2%F3%B2%E2%F3%E0%E6%FB%E0%B2%F6%F7%B2%FE%F3%B2%F6%F7%F4%FB%FC%FB%F1%FBa%FC%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F1a%FF%FD%B2%E1%F7%B2%F1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%FF%F1%FF%B2%F4%F3%F1%E6%FD%E0%FB%E8%F3%FC%F6%FD%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%D7%FC%F1%F3%F6%F7%FC%F3%B2%FF%F1%FF%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F1a%FF%FD%B2%E1%F7%B2%F1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%FF%F1%FF%B2%F6%F7%B2%FFs%E1%B2%F6%F7%B2%F6%FD%E1%B2%F1%F3%FC%E6%FB%F6%F3%F6%F7%E1%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%DF%F1%FF%B2%F1%FD%FC%B2%F1%F3%FE%F1%E7%FE%F3%F6%FD%E0%F3%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FC%FD%E8%F1%FD%B2%F1a%FF%FD%B2%E1%F7%B2%F1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%FF%F1%FF%B2%F1%FD%FC%B2%F1%F3%FE%F1%E7%FE%F3%F6%FD%E0%F3%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%D3%FE%E7%FF%F0%E0%F3%FC%F6%FD%B2%F7%FE%B2%E2%F3%E1%F7%FD%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DB%F6%F7%FC%E6%FB%F4%FB%F1%FD%B2%E7%FC%B2%E2%E0%FD%F0%FE%F7%FF%F3%B2%F6%F7%B2%F1%FD%FB%FC%F1%FB%F6%F7%FC%F1%FB%F3%E1%B2%F6%F7%B2%FFh%FE%E6%FB%E2%FE%FD%E1%B2%F7%FC%B2%E7%FC%B2%F7%FC%E6%FD%E0%FC%FD%B2%E0%F7%F3%FE%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%C2%E0%F3%F1%E6%FB%F1%F3%B2%F7%FE%B2%FF%F1%FF%B2%F6%F7%B2%F6%FD%E1%B2%FCh%FF%F7%E0%FD%E1%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DF%F7%F1%F3%FC%FB%E8%FD%B2%F7%FE%B2%F1s%FE%F1%E7%FE%FD%B2%FF%F7%FC%E6%F3%FE%B2%F6%F7%FE%B2%FF%F1%FF%B2%F6%F7%B2%F6%FD%E1%B2%F1%F3%FC%E6%FB%F6%F3%F6%F7%E1%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%CF%BE%B0%FA%F3%E1%DE%FD%F5%FD%B0%A8%F4%F3%FE%E1%F7%BE%B0%E7%E0%FE%DE%FD%F5%FD%B0%A8%B0%B0%BE%B0%FA%F3%E1%D1%FD%FF%FF%E7%FC%FB%E6%EB%B0%A8%E6%E0%E7%F7%BE%B0%E7%E0%FE%D1%FD%FF%FF%E7%FC%FB%E6%EB%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%DE%DD%D5%DD%CD%D1%C0%D7%D3%D5%D3%DE%BC%A3%BC%E2%FC%F5%B0%BE%B0%FA%F3%E1%D6%F7%F1%FD%E0%F3%E6%FB%E4%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%E7%E0%FE%D6%F7%F1%FD%E0%F3%E6%FB%E4%F7%B0%A8%B0%B0%BE%B0%E1%F3%E4%F7%D6%F3%E6%F3%B0%A8%E6%E0%E7%F7%BE%B0%E7%E1%F7%E0%D6%F3%E6%F3%B0%A8%E6%E0%E7%F7%BE%B0%F4%FD%FD%E6%F7%E0%B0%A8%B0%D7%E1%E6%F3%B2%AE%F3%B2%FA%E0%F7%F4%AF%FA%E6%E6%E2%E1%A8%BD%BD%F7%E1%BC%E5%FB%F9%FB%E2%F7%F6%FB%F3%BC%FD%E0%F5%BD%E5%FB%F9%FB%BD%DE%FB%E1%E6%F3%CD%F6%F7%CD%F1%FD%FF%E2%E0%FD%F0%F3%F1%FB%B7%D1%A1%B7%D0%A1%FC%AC%FE%FB%E1%E6%F3%B2%F6%F7%B2%F1%FD%E6%F7%F8%FD%AE%BD%F3%AC%B2%E1%F7%B2%F7%FC%F1%E7%F7%FC%E6%E0%F3%B2%F0%F3%F8%FD%B2%E7%FC%F3%B2%FE%FB%F1%F7%FC%F1%FB%F3%AE%BD%F0%E0%AC%AE%F3%B2%FA%E0%F7%F4%AF%FA%E6%E6%E2%E1%A8%BD%BD%F1%E0%F7%F3%E6%FB%E4%F7%F1%FD%FF%FF%FD%FC%E1%BC%FD%E0%F5%BD%FE%FB%F1%F7%FC%E1%F7%E1%BD%F0%EB%BF%FC%F1%BF%E1%F3%BD%A6%BC%A2%BD%F6%F7%F7%F6%BC%F5%FE%AC%D1%E0%F7%F3%E6%FB%E4%F7%B2%D1%FD%FF%FF%FD%FC%E1%B2%C0%F7%F1%FD%FC%FD%F1%FB%FF%FB%F7%FC%E6%FD%B2%DC%FD%B2%F1%FD%FF%F7%E0%F1%FB%F3%FE%BF%D1%FD%FF%E2%F3%E0%E6%FB%E0%B2%FB%F5%E7%F3%FE%B2%A6%BC%A2%B2%AE%BD%F3%AC%B0%BE%B0%E7%E1%F7%C1%F1%FD%E0%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%D1%FD%FF%E2%FE%FB%E6%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B0%BE%B0%FF%E1%F5%D6%FD%FC%F7%B0%A8%B0%DA%F7%F1%FA%FD%B0%BE%B0%FF%E1%F5%DB%FC%C2%E0%FD%F5%E0%F7%E1%E1%B0%A8%B0%D7%FC%B2%E2%E0%FD%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C7%FC%E0%F7%F3%FE%FB%E8%F7%F6%B0%A8%B0%C1%FB%FC%B2%F1%FD%FF%E2%FE%F7%E6%F3%E0%B0%BE%B0%FF%E1%F5%E6%F3%E1%F9%DC%E7%FF%F0%F7%E0%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E6%F3%E0%F7%F3%E1%B0%BE%B0%FF%E1%F5%DC%F3%FF%F7%B0%A8%B0%DC%FD%FF%F0%E0%F7%B0%BE%B0%FF%E1%F5%D6%F3%E6%F7%B0%A8%B0%D4%F7%F1%FA%F3%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%B0%A8%B0%D6%F7%E1%F1%F3%E0%F5%F3%E0%B0%BE%B0%FF%E1%F5%DE%FB%E1%E6%B0%A8%B0%FE%FB%E1%E6%F3%CD%F6%F7%CD%F1%FD%E6%F7%F8%FD%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%E1%B0%A8%B0%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%B0%A8%B0%E2%E7%FC%E6%FD%B0%BE%B0%FF%E1%F5%C0%F7%F0%FD%FD%E6%B0%A8%B0%C0%F7%FB%FC%FB%F1%FB%F3%E0%B0%BE%B0%FF%E1%F5%D6%F7%FE%F7%E6%F7%B0%A8%B0-%C1%F7%F5%E7%E0%FD%B2%E3%E7%F7%B2%F6%F7%E1%F7%F3%B2%F0%FD%E0%E0%F3%E0%B2%E6%FD%F6%FD%E1%B2%FE%FD%E1%B2%F1%F3%FF%E2%FD%E1%B2%F6%F7%FE%B2%F4%FD%E0%FF%E7%FE%F3%E0%FB%FD%AD%B0%EF%EF
Navegador incompatible
Cuando hayas completado esta lista podrás pasar al apartado siguiente.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0