3.11. Harinas de Galicia

Empaquetando la molienda

Cuencos con harina de trigo y de maiz sobre un mantel con motivos del mar

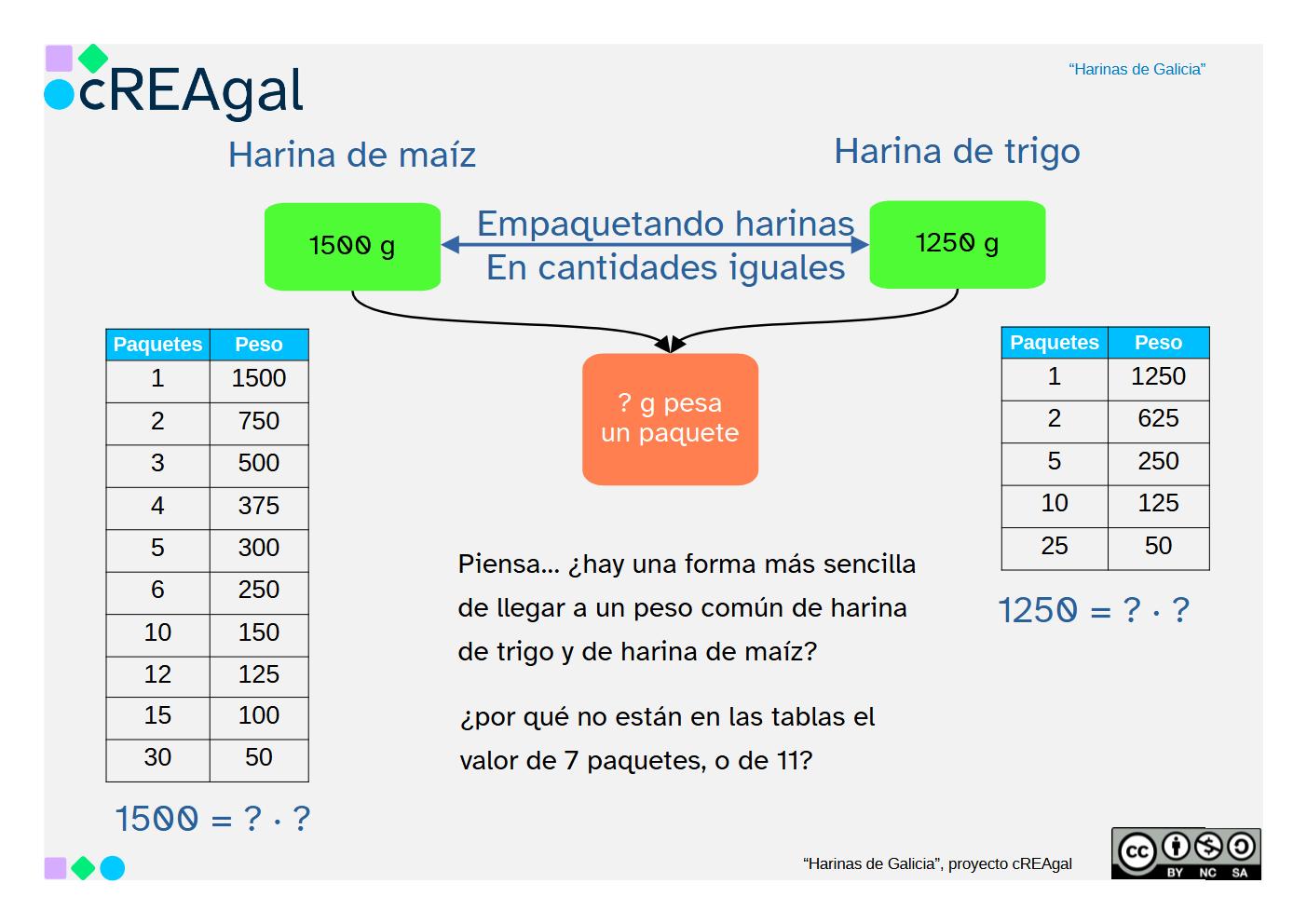
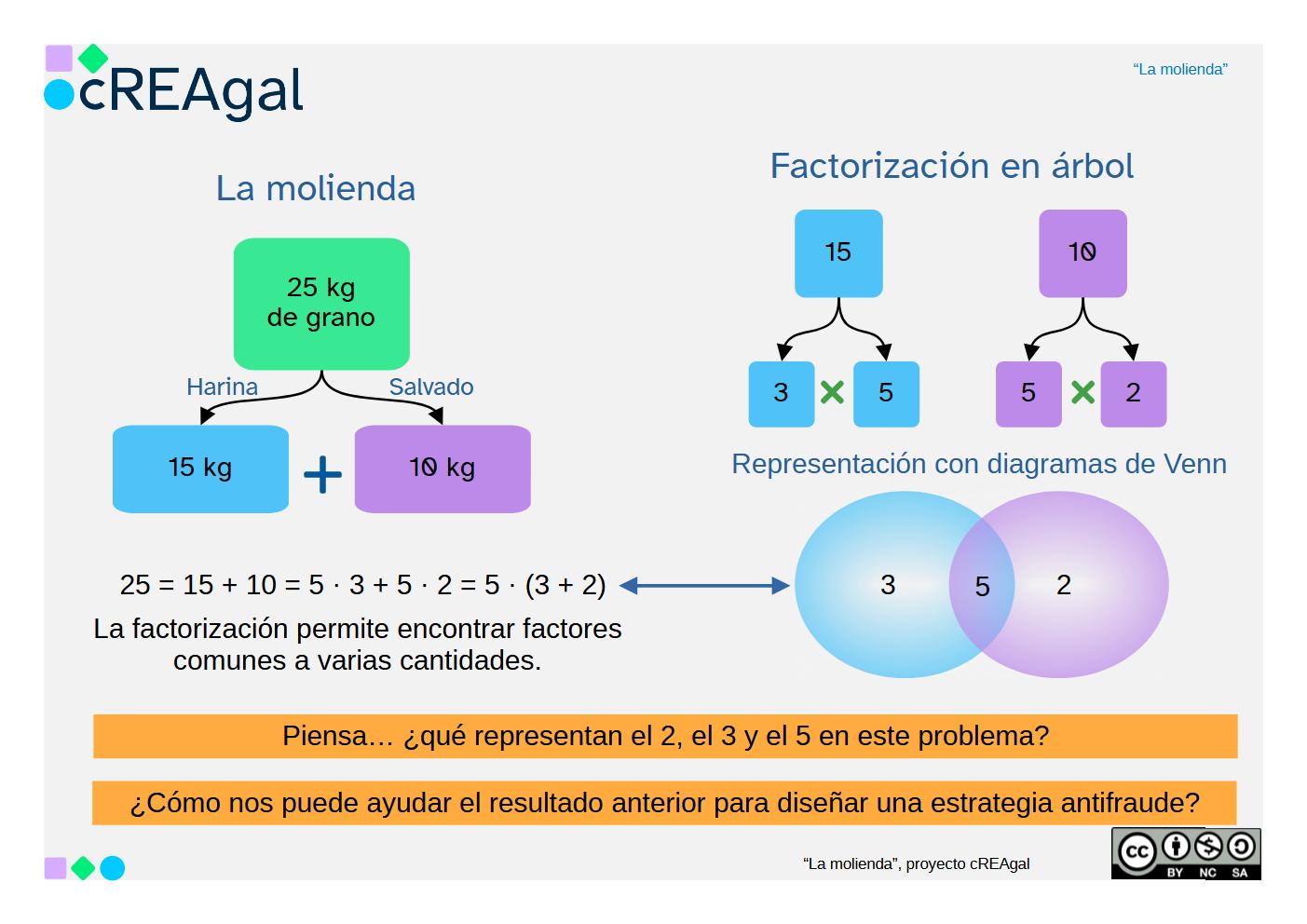
En la molienda, el grano se separa en sus dos componentes, la harina y el salvado, que luego se guardan en sacos.

Para formar sacos que tengan el mismo peso hay que dividir entre ese valor.

Si no conocemos un peso concreto, pero sabemos que todos deben pesar lo mismo y de forma exacta, calcularemos divisores.

Si comparamos dos o más clases de harina diferentes para formar paquetes iguales, estaremos comparando sus divisores.

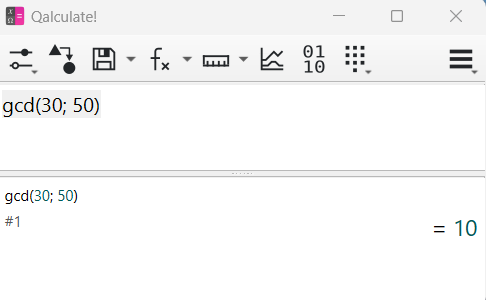
Habitualmente se busca el mayor de todos ellos, o lo que es lo mismo:

el máximo común divisor.

Definición:

Llamamos máximo común divisor de dos o más números al mayor de todos sus divisores comunes.

Lectura facilitada

En la molienda el grano se separa en harina y el salvado.

Luego se guardan en sacos.

Para formar sacos que tengan el mismo peso hay que dividir entre ese peso.

Calculamos divisores cuando buscamos que todos los sacos pesen lo mismo.

Comparamos divisores de dos números cuando buscamos formar paquetes iguales de dos tipos de harinas.

Habitualmente se busca el mayor de todos ellos:

el máximo común divisor.

Definición:

Llamamos máximo común divisor de dos o más números al mayor de todos sus divisores comunes.

Harinas de Galicia

Cuencos con harina de trigo y harina de maíz

Investiga:

Queremos hacer paquetes promocionales de harinas de Galicia.

Disponemos de:

1500 g de harina de maíz
1250 g de harina de trigo

Todos los paquetes deben pesar lo mismo (los de harina de maíz lo mismo que los de harina de trigo).

Calcula cuántos paquetes obtendrás teniendo en cuenta que deben llevar la mayor cantidad de gramos de harina posible (descarta los que estén por debajo de 100 gramos ya que serían demasiado pequeños).

Pista 1

Antes de calcular el número de envases tenemos que saber qué cantidad de harina contendrá cada uno.

Para comprender mejor el reparto de la harina en paquetes podemos hacer una tabla que nos ayude a ordenarlos por peso, de mayor a menor cantidad, tanto de maíz como de trigo.

Calculamos todos los divisores de cada una de las dos cantidades dividiendo entre 1, 2, 3, 4, 5... y seleccionando los cocientes de divisiones exactas.

Descartamos los que están por debajo de 100 gramos ya que serían paquetes muy pequeños.

Peso de cada paquete en gramos
Maíz	1500	750	500	375	300	250	175	150	125	100
Trigo	1250	625	250	125

Pista 2

En la tabla anterior elige un divisor que sea común de la cantidad de maíz y de trigo.

Si hubiese más de uno tendríamos que elegir el mayor de ellos.

Esquema del problema

Este esquema te ayudará a entender mejor cómo abordar un problema de este tipo:

Esquema del problema Harinas de Galicia

La molienda

Salvado cayendo a través de la tolva a un ferrado

En la molienda del grano se separa en dos partes, la harina y el salvado.

Por ejemplo:

Si molemos 25 kg de grano obtenemos 10 kg de salvado y 15 de harina.

Investiga:

Factoriza 10 y 15 e interpreta los factores que aparecen en ambos números en el contexto de este problema.
¿Qué representa el resultado del mcd (10, 15)?

Utilizando el resultado anterior, responde:

qué cantidad de harina obtenemos en 5 kg de grano.
qué cantidad de salvado obtenemos en 5 kg de grano.

Bajo sospecha...

Xiana llevó un saco de grano al molino y se olvidó de pesarlo.

Piensa que seguramente eran más de 30 kg porque era una saca de 50 kg y superaba la mitad.

Está preocupada, porque sospecha que la persona que lleva el molino le da el salvado que le corresponde, pero se queda siempre con algo de la harina a pesar de que le paga 10 euros por la molienda.

¿Cómo puede comprobar si esto es cierto?

Crea una estrategia para detectar posibles fraudes en las cantidades de harina recogida.

Esquema del problema

Este esquema puede ayudaros a resolver el problema:

Esquema del problema

Fichas para hacer los problemas de grupo

El arte de calcular el máximo común divisor

En la sección 3.9. se describen "algoritmos" para calcular en mcm.

Ahora nos toca estudiar algunas formas de calcular el máximo común divisor.

Por definición

Este algoritmo se basa en la definición de máximo común divisor de dos o más números, como el mayor de todos sus divisores comunes.

Por tanto:

INICIO DEL ALGORITMO

PASO 1: hacemos una lista con los divisores de cada número de mayor a menor.
PASO 2: buscamos la primera coincidencia entre los listados anteriores, es decir, el mayor divisor común.

FIN DEL ALGORITMO

Cualquier otra coincidencia es un divisor común pero ya no sería el mayor de todos.

Factorizando

Este algoritmo se basa en que cualquier divisor de un número se forma multiplicando sus divisores (factores).

Por tanto, el divisor común se formará multiplicando factores que están en ambos números.

Ejemplo:

Calcular el mcd (50, 30)

INICIO DEL ALGORITMO

PASO 1: factorizamos cada uno de los números.

50 = 5 · 10 = 5 · 5 · 2

30 = 3 · 10 = 3 · 5 · 2

PASO 2: identificamos los factores que están en los dos números simultáneamente.

Un 5 y un 2 están en ambas factorizaciones.

PASO 3: multiplicamos esos factores y obtenemos el máximo común divisor.

El mcd es 5 · 2 = 10

FIN DEL ALGORITMO

Si expresamos los factores repetidos en forma de potencia debemos prestar atención a los exponentes y no poner más de los que están en ambos números simultáneamente.

Entre 5² y 5¹ elegiríamos 5¹porque en la factorización de 30 el 5 aparece sólo una vez.

mcd (30, 50) = 5¹ · 2¹

Mcd con calculadora

Captura de pantalla del cálculo del mcd con calculadora

Las calculadoras actuales, tanto físicas como el software de ordenador, permiten calcular el máximo común divisor.

Para ello debes mirar en el manual de instrucciones o en la ayuda cómo funciona.

En el ejemplo de la imagen utilizamos la calculadora Qalculate!, que de forma sencilla nos halla el mcd.

Las iniciales gcd se corresponden con la traducción en inglés de máximo común divisor:

greatest common divisor.

Otro software que permite hallar el mcd es geogebra.

Los dos programas anteriores permiten calcular simultáneamente el mcd de más de dos cantidades, pero no siempre ocurre.

En ese caso podrías utilizar el mismo método en cadena que explicamos para el mcm.

Euclides nos ayuda con el mcd

Algoritmo de Euclides

El algoritmo de Euclides permite calcular el mcd de dos números mediante divisiones encadenadas.

Veámoslo con un ejemplo:

Calcula el mcd (50, 30)

INICIO DEL ALGORITMO

PASO 1: dividimos 50 : 30 el cociente es 1 y el resto es 20

como la división no es exacta dividimos el divisor entre el resto.

PASO 2: dividimos 30 : 20 el cociente es 1 y el resto es 10

como la división no es exacta dividimos el divisor entre el resto.

PASO 3: dividimos 20 : 10 el cociente es 2 y el resto es 0

Al llegar a la división exacta el último divisor es el número que buscamos.

El resultado del mcd (50, 30) es 10.

FIN DEL ALGORITMO

Diagrama de flujo

Cualquier algoritmo puede expresarse mediante un diagrama de flujo en el que se van dibujando los pasos que hay que realizar.

Algoritmo de Euclides

En el algoritmo de Euclides primero dividimos el mayor de los dos números entre el menor.

Nos preguntamos ¿el resto es 0?

En caso afirmativo hemos terminado, ya tenemos el máximo común divisor.

En caso negativo volvemos a dividir, esta vez el divisor entre el resto anterior.

Y repetimos la pregunta, ¿el resto es 0?

Si la repuesta es negativa continuamos hasta que la respuesta sea "sí".

Se trata de un procedimiento sencillo repetitivo que además es fácil de memorizar.

Engrana el mdc y el mcm

Inventor con engranajes

Acabas de ver qué fácil es calcular el máximo común divisor usando el algoritmo de Euclides, pues ahora viene lo mejor.

¿Te parece complicado calcular el mínimo común múltiplo?

Hay una propiedad que te puede ayudar, es la siguiente:

mcd (a,b) · mcm (a,b) = a · b

El producto del máximo común divisor por el mínimo común múltiplo de dos números es igual al producto de ambos números.

Por lo tanto, si sabes el máximo común divisor podrías hallar el mínimo común múltiplo a partir de él con esta propiedad.

En el ejemplo anterior:

50 · 30 = 1500

el mcd (30, 50) = 10

Entonces el mcm (30, 50) = 150

ya que 1500 : 10 =150

¡Cómo raya!

El tiburón y la raya

¿Sabes qué tienen en común las rayas y los tiburones?

Son los vertebrados más antiguos, habitan la tierra desde hace más de 400 millones de años.
Son cartilaginosos, no tienen espinas.
Ambos tienen dientes que van cambiando...

Pero también hay diferencias:

hay muchas más clases de rayas que de tiburones, 650 frente a 530.
las rayas tienen las aletas fusionadas a la cabeza...

Si estudias las características de varias especies encontrarás elementos comunes y diferencias.

Todas forman parte de su descripción.

Según tu interés elegirás unas u otras.

Los números

Lo mismo ocurre al estudiar conjuntamente dos o más números.

Cuando hacemos su factorización prima hay coincidencias y diferencias.

Elegiremos unas u otras según el estudio que queramos hacer.

A continuación, te contamos otra forma más para construir el máximo común divisor o el mínimo común múltiplo de dos o más números a partir de su factorización prima.

El mcd y el mcm

Si queremos hallar el máximo común divisor nos fijamos en las coincidencias:

El máximo común divisor de dos cantidades se halla multiplicando todos los factores primos comunes elevados al menor exponente.

Halla el mcd de 40 y 60.

40 = 2³ · 5

60 = 2² · 5 · 3

mcd (40, 60) = 2² · 5 = 20

Si queremos hallar el mínimo común múltiplo nos fijamos en coincidencias y diferencias:

El mínimo común múltiplo de dos cantidades se halla multiplicando todos los factores primos, comunes y no comunes, elevados al mayor exponente.

Halla el mcm de 40 y 60.

40 = 2³ · 5

60 = 2² · 5 · 3

mcm (40, 60) = 2³ · 5 · 3 = 120

Practica mcd de dos números

Practica el cálculo del máximo común divisor de dos números con este applet.

Cada respuesta correcta suma 2 puntos, y cada fallo resta 1 punto. La puntuación máxima es 10.

https://www.geogebra.org/m/mtnqvqyz (Ventana nueva)

(Guardar la puntuación)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/mtnqvqyz,GG_MAT1ESO_REA01%20MCD%20de%20dos%20n%FAmeros,1,Autor%EDa

Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Repasa las definiciones de mcm y mcd

Mínimo común múltiplo de dos o más números

Llamamos mínimo común múltiplo de dos o más números, al menor de sus múltiplos comunes.

Máximo común divisor de dos o más números

Llamamos máximo común divisor de dos o más números, al mayor de sus divisores comunes.

Propiedad que relaciona el mcm y el mcd de dos números

El producto del máximo común divisor por el mínimo común múltiplo de dos números es igual al producto de ambos números.

mcd (a,b) · mcm (a,b) = a · b

Algoritmo de Euclides

Método para calcular el mcd de dos números.

Lista de cotejo de mcd

Completa la lista de cotejo marcando las casillas al realizar las actividades correspondientes.

%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%E6%F7%F8%FD%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A6%A6%A6%A6%A7%A6%AA%BF%A3%A0%A2%B0%BE%B0%E6%FB%E6%FE%F7%B0%A8%B0%A1%BC%A3%A3%B2%DA%F3%E0%FB%FC%F3%E1%B2%F6%F7%B2%D5%F3%FE%FB%F1%FB%F3%BC%B0%BE%B0%E1%E7%F0%E6%FB%E6%FE%F7%B0%A8%B0%D1%FD%FF%E2%E0%E7%F7%F0%F3%B2%E1%FB%B2%FA%F3%E1%B2%F7%FC%E6%F7%FC%F6%FB%F6%FD%B2%FE%F3%E1%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%F7%E1%B2%EB%B2%F1%FD%FC%E6%F7%FC%FB%F6%FD%E1%B2%F3%FC%E6%F7%E0%FB%FD%E0%F7%E1%B0%BE%B0%FE%F7%E4%F7%FE%E1%B0%A8%C9%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%AA%BC%A4%A4%A4%A5%E2%EA%A9%CE%B0%AC%D7%FF%E2%F3%E3%E7%F7%E6%F3%FC%F6%FD%B2%FE%F3%B2%FF%FD%FE%FB%F7%FC%F6%F3%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%FE%F3%B2%F6%F7%F4%FB%FC%FB%F1%FBa%FC%B2%F6%F7%B2%FF%F1%F6%B2%F3%E2%FE%FB%F1%F3%F6%F3%B2%F3%B2%E7%FC%B2%F1%FD%FC%E6%F7%EA%E6%FD%B2%E0%F7%F3%FE%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%AA%BC%A4%A4%A4%A5%E2%EA%A9%CE%B0%AC%DA%F3%E0%FB%FC%F3%E1%B2%F6%F7%B2%D5%F3%FE%FB%F1%FB%F3%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DB%FC%E6%F7%E0%E2%E0%F7%E6%FD%B2%E7%FC%B2%F7%FC%E7%FC%F1%FB%F3%F6%FD%B2%F6%F7%B2%F1%FD%FB%FC%F1%FB%F6%F7%FC%F1%FB%F3%B2%F6%F7%B2%F6%FB%E4%FB%E1%FD%E0%F7%E1%B2%F6%F7%B2%F6%FD%E1%B2%F1%F3%FC%E6%FB%F6%F3%F6%F7%E1%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%DE%F3%B2%FF%FD%FE%FB%F7%FC%F6%F3%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DB%F6%F7%FC%E6%FB%F4%FB%F1%FD%B2%FE%F3%B2%E2%E0%FD%E2%FD%E0%F1%FBa%FC%B2%F6%F7%B2%FA%F3%E0%FB%FC%F3%B2%EB%B2%F6%F7%B2%E1%F3%FE%E4%F3%F6%FD%B2%E3%E7%F7%B2%E1%F7%B2%FD%F0%E6%FB%F7%FC%F7%B2%F3%FE%B2%FF%FD%FE%F7%E0%B2%F7%FE%B2%F5%E0%F3%FC%FD%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%E3%E7%7B%B2%E1%FB%F5%FC%FB%F4%FB%F1%F3%B2%F7%FE%B2%FF%F1%F6%B2%F7%FC%B2%F7%E1%E6%F7%B2%E2%E0%FD%F0%FE%F7%FF%F3%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D3%E2%FE%FB%F1%FD%B2%F7%FE%B2%FF%F1%F6%B2%E2%F3%E0%F3%B2%E0%F7%E1%FD%FE%E4%F7%E0%FE%FD%B2%EB%B2%FE%FD%B2%FB%FC%E6%F7%E0%E2%E0%F7%E6%FD%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%D7%FE%B2%F3%E0%E6%F7%B2%F6%F7%B2%F1%F3%FE%F1%E7%FE%F3%E0%B2%F7%FE%B2%FF%F1%F6%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%CE%B0%AC%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F1a%FF%FD%B2%E1%F7%B2%F1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%FF%F1%F6%B2%F3%B2%E2%F3%E0%E6%FB%E0%B2%F6%F7%B2%FE%F3%B2%F6%F7%F4%FB%FC%FB%F1%FBa%FC%BC%AE%BD%E1%E2%F3%FC%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%CE%B0%AC%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F1a%FF%FD%B2%E1%F7%B2%F1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%FF%F1%F6%B2%F4%F3%F1%E6%FD%E0%FB%E8%F3%FC%F6%FD%BC%AE%BD%E1%E2%F3%FC%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%DF%F1%F6%B2%F1%FD%FC%B2%F1%F3%FE%F1%E7%FE%F3%F6%FD%E0%F3%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%F1a%FF%FD%B2%E1%F7%B2%F1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%FF%F1%F6%B2%F1%FD%FC%B2%F1%F3%FE%F1%E7%FE%F3%F6%FD%E0%F3%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%D7%E7%F1%FE%FB%F6%F7%E1%B2%FC%FD%E1%B2%F3%EB%E7%F6%F3%B2%F1%FD%FC%B2%F7%FE%B2%FF%F1%F6%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FF%E2%E0%F7%FC%F6%FD%B2%EB%B2%F3%E2%FE%FB%F1%FD%B2%F7%FE%B2%F3%FE%F5%FD%E0%FB%E6%FF%FD%B2%F6%F7%B2%D7%E7%F1%FE%FB%F6%F7%E1%B2%E2%F3%E0%F3%B2%FA%F3%FE%FE%F3%E0%B2%F7%FE%B2%FF%F1%F6%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%D1%FD%FC%FD%E8%F1%FD%B2%FE%F3%B2%E2%E0%FD%E2%FB%F7%F6%F3%F6%B2%E3%E7%F7%B2%E2%F7%E0%FF%FB%E6%F7%B2%FA%F3%FE%FE%F3%E0%B2%F7%FE%B2%FF%F1%FF%B2%F1%FD%FC%FD%F1%FB%F6%FD%B2%F7%FE%B2%FF%F1%F6%B2%EB%B2%E4%FB%F1%F7%E4%F7%E0%E1%F3%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC3%D1a%FF%FD%B2%E0%F3%EB%F3%B3%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%DB%F6%F7%FC%E6%FB%F4%FB%F1%FD%B2%E1%FB%FF%FB%FE%FB%E6%E7%F6%F7%E1%B2%EB%B2%F6%FB%F4%F7%E0%F7%FC%F1%FB%F3%E1%B2%F7%FC%B2%FE%FD%E1%B2%F3%FE%F5%FD%E0%FB%E6%FF%FD%E1%B2%E3%E7%F7%B2%E2%F7%E0%FF%FB%E6%F7%FC%B2%F1%F3%FE%F1%E7%FE%F3%E0%B2%F7%FE%B2%FF%F1%F6%B2%EB%B2%F7%FE%B2%FF%F1%FF%B2%F3%B2%E2%F3%E0%E6%FB%E0%B2%F6%F7%B2%FE%F3%B2%F4%F3%F1%E6%FD%E0%FB%E8%F3%F1%FBa%FC%B2%E2%E0%FB%FF%F3%BC%AE%F0%E0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%C2%E0%F3%F1%E6%FB%F1%F3%B2%F7%FE%B2%FF%F1%F6%B2%F6%F7%B2%F6%FD%E1%B2%FCh%FF%F7%E0%FD%E1%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%CE%B0%AC%DF%F7%F1%F3%FC%FB%E8%FD%B2%F7%FE%B2%F1s%FE%F1%E7%FE%FD%B2%FF%F7%FC%E6%F3%FE%B2%F6%F7%FE%B2%FF%F1%F6%B2%F6%F7%B2%F6%FD%E1%B2%F1%F3%FC%E6%FB%F6%F3%F6%F7%E1%BC%AE%BD%E1%E2%F3%FC%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A1%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A2%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%FA%A0%B2%F1%FE%F3%E1%E1%AF%CE%B0%E5%F7%E1%E6%F7%E0%FC%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%FF%F3%E0%F5%FB%FC%BF%E6%FD%E2%A8%B2%A2%BC%A3%A3%F1%FF%A9%B2%FF%F3%E0%F5%FB%FC%BF%F0%FD%E6%E6%FD%FF%A8%B2%A2%BC%A3%A3%F1%FF%CE%B0%AC%AE%E1%E6%E0%FD%FC%F5%AC%AE%F4%FD%FC%E6%B2%F1%FD%FE%FD%E0%AF%CE%B0%B1%A2%A2%A5%F0%F1%A6%CE%B0%AC%AE%F4%FD%FC%E6%B2%E1%FB%E8%F7%AF%CE%B0%A6%CE%B0%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A3%A6%E2%E6%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E5%F7%FB%F5%FA%E6%A8%B2%FC%FD%E0%FF%F3%FE%CE%B0%AC%C0%F7%E2%F3%E1%F3%B2%FE%F3%E1%B2%F6%F7%F4%FB%FC%FB%F1%FB%FD%FC%F7%E1%B2%F6%F7%B2%FF%F1%FF%B2%EB%B2%FF%F1%F6%AE%F0%E0%AC%AE%BD%E1%E2%F3%FC%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%F4%FD%FC%E6%AC%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%FA%A0%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%B0%A2%B0%BE%B0%FC%FB%E4%F7%FE%B0%A8%B0%A3%B0%BE%B0%FB%E6%F7%FF%B0%A8%B0%AE%E1%E6%E0%FD%FC%F5%B2%E1%E6%EB%FE%F7%AF%CE%B0%F1%FD%FE%FD%E0%A8%B2%E0%F5%F0%BA%A2%BE%B2%A2%BE%B2%A2%BB%A9%B2%F4%FD%FC%E6%BF%F4%F3%FF%FB%FE%EB%A8%B2%B4%E3%E7%FD%E6%A9%D3%E6%F9%FB%FC%E1%FD%FC%B2%DA%EB%E2%F7%E0%FE%F7%F5%FB%F0%FE%F7%B4%E3%E7%FD%E6%A9%A9%B2%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%FF%F7%F6%FB%E7%FF%A9%B2%FE%F7%E6%E6%F7%E0%BF%E1%E2%F3%F1%FB%FC%F5%A8%B2%A2%BC%A7%E2%EA%A9%CE%B0%AC%D6%F7%F4%FB%FC%FB%F1%FB%FD%FC%F7%E1%B2%E0%F7%E2%F3%E1%F3%F6%F3%E1%BC%AE%BD%E1%E6%E0%FD%FC%F5%AC%B0%BE%B0%E2%FD%FB%FC%E6%E1%B0%A8%B0%B0%EF%CF%BE%B0%FA%F3%E1%DE%FD%F5%FD%B0%A8%F4%F3%FE%E1%F7%BE%B0%E7%E0%FE%DE%FD%F5%FD%B0%A8%B0%B0%BE%B0%FA%F3%E1%D1%FD%FF%FF%E7%FC%FB%E6%EB%B0%A8%E6%E0%E7%F7%BE%B0%E7%E0%FE%D1%FD%FF%FF%E7%FC%FB%E6%EB%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%DE%DD%D5%DD%CD%D1%C0%D7%D3%D5%D3%DE%BC%A3%BC%E2%FC%F5%B0%BE%B0%FA%F3%E1%D6%F7%F1%FD%E0%F3%E6%FB%E4%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%E7%E0%FE%D6%F7%F1%FD%E0%F3%E6%FB%E4%F7%B0%A8%B0%B0%BE%B0%E1%F3%E4%F7%D6%F3%E6%F3%B0%A8%E6%E0%E7%F7%BE%B0%E7%E1%F7%E0%D6%F3%E6%F3%B0%A8%E6%E0%E7%F7%BE%B0%F4%FD%FD%E6%F7%E0%B0%A8%B0%D7%E1%E6%F3%B2%AE%F3%B2%FA%E0%F7%F4%AF%FA%E6%E6%E2%E1%A8%BD%BD%F7%E1%BC%E5%FB%F9%FB%E2%F7%F6%FB%F3%BC%FD%E0%F5%BD%E5%FB%F9%FB%BD%DE%FB%E1%E6%F3%CD%F6%F7%CD%F1%FD%FF%E2%E0%FD%F0%F3%F1%FB%B7%D1%A1%B7%D0%A1%FC%AC%FE%FB%E1%E6%F3%B2%F6%F7%B2%F1%FD%E6%F7%F8%FD%AE%BD%F3%AC%B2%E1%F7%B2%F7%FC%F1%E7%F7%FC%E6%E0%F3%B2%F0%F3%F8%FD%B2%E7%FC%F3%B2%FE%FB%F1%F7%FC%F1%FB%F3%AE%BD%F0%E0%AC%AE%F3%B2%FA%E0%F7%F4%AF%FA%E6%E6%E2%E1%A8%BD%BD%F1%E0%F7%F3%E6%FB%E4%F7%F1%FD%FF%FF%FD%FC%E1%BC%FD%E0%F5%BD%FE%FB%F1%F7%FC%E1%F7%E1%BD%F0%EB%BF%FC%F1%BF%E1%F3%BD%A6%BC%A2%BD%F6%F7%F7%F6%BC%F5%FE%AC%D1%E0%F7%F3%E6%FB%E4%F7%B2%D1%FD%FF%FF%FD%FC%E1%B2%C0%F7%F1%FD%FC%FD%F1%FB%FF%FB%F7%FC%E6%FD%B2%DC%FD%B2%F1%FD%FF%F7%E0%F1%FB%F3%FE%BF%D1%FD%FF%E2%F3%E0%E6%FB%E0%B2%FB%F5%E7%F3%FE%B2%A6%BC%A2%B2%AE%BD%F3%AC%B0%BE%B0%E7%E1%F7%C1%F1%FD%E0%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%D1%FD%FF%E2%FE%FB%E6%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B0%BE%B0%FF%E1%F5%D6%FD%FC%F7%B0%A8%B0%DA%F7%F1%FA%FD%B0%BE%B0%FF%E1%F5%DB%FC%C2%E0%FD%F5%E0%F7%E1%E1%B0%A8%B0%D7%FC%B2%E2%E0%FD%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C7%FC%E0%F7%F3%FE%FB%E8%F7%F6%B0%A8%B0%C1%FB%FC%B2%F1%FD%FF%E2%FE%F7%E6%F3%E0%B0%BE%B0%FF%E1%F5%E6%F3%E1%F9%DC%E7%FF%F0%F7%E0%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E6%F3%E0%F7%F3%E1%B0%BE%B0%FF%E1%F5%DC%F3%FF%F7%B0%A8%B0%DC%FD%FF%F0%E0%F7%B0%BE%B0%FF%E1%F5%D6%F3%E6%F7%B0%A8%B0%D4%F7%F1%FA%F3%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%B0%A8%B0%D6%F7%E1%F1%F3%E0%F5%F3%E0%B0%BE%B0%FF%E1%F5%DE%FB%E1%E6%B0%A8%B0%FE%FB%E1%E6%F3%CD%F6%F7%CD%F1%FD%E6%F7%F8%FD%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%E1%B0%A8%B0%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%B0%A8%B0%E2%E7%FC%E6%FD%B0%BE%B0%FF%E1%F5%C0%F7%F0%FD%FD%E6%B0%A8%B0%C0%F7%FB%FC%FB%F1%FB%F3%E0%B0%BE%B0%FF%E1%F5%D6%F7%FE%F7%E6%F7%B0%A8%B0-%C1%F7%F5%E7%E0%FD%B2%E3%E7%F7%B2%F6%F7%E1%F7%F3%B2%F0%FD%E0%E0%F3%E0%B2%E6%FD%F6%FD%E1%B2%FE%FD%E1%B2%F1%F3%FF%E2%FD%E1%B2%F6%F7%FE%B2%F4%FD%E0%FF%E7%FE%F3%E0%FB%FD%AD%B0%EF%EF

Navegador non compatible

Cuando hayas completado esta lista podrás pasar al apartado siguiente.

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0