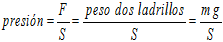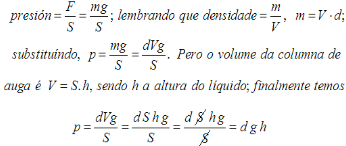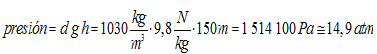2.3.2 Presión no interior dun líquido en repouso
Experiencia práctica
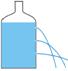
- Colla unha botella de plástico de dous litros (refresco, auga mineral…) e fágalle varios buratos a distinta altura; procure que os buratos sexan todos aproximadamente iguais. Encha a botella de auga e observe como sae polos buratiños.
- Xa ve que canto maior sexa a profundidade en que estea o orificio, con máis velocidade sairá a auga por el. Isto é así porque dentro do líquido hai presión, e esta presión empurra a auga que sae polo burato; tamén deducimos que a presión aumenta coa profundidade.
- Imaxine que facemos unha torre de ladrillos; esta torre fai presión contra o chan porque os ladrillos pesan, e esta forza está repartida nunha superficie, a do ladrillo inferior en contacto con chan. É máis, podemos calcular esta presión con esta fórmula, onde m é a masa dos ladrillos:
- Se no canto dunha torre de ladrillos temos unha columna de auga ou doutro líquido, a situación é a mesma: no fondo do líquido hai presión porque o líquido pesa, e este peso está repartido na superficie do fondo.
- Podemos tamén calcular o valor da presión do líquido contra o fondo, é moi parecido ao caso dos ladrillos:
presión = d.g.h
Xa que logo, a presión exercida por un líquido é proporcional á densidade do líquido e á profundidade, como xa comprobáramos na experiencia da botella. Podemos medir directamente cun manómetro de mercurio a presión dentro dun líquido a diversas profundidades, e comprobar o anterior.
Unha consecuencia de que a presión só depende da profundidade é que a superficie libre (a de arriba) dos líquidos en repouso é plana e horizontal. Estamos afeitos a velo, pero por que é así?
Imaxine que non fose, como no vaso da figura; daquela, no punto A habería máis presión que no punto B, xa que A ten máis altura de auga enriba, e as moléculas do líquido estarían máis comprimidas en A que en B. Xa que logo, as moléculas en A empurran máis cara á esquerda que as de B cara á dereita, así que as da zona A se moven en dirección a B, ata que a presión nas dúas zonas se iguala: e isto ocorre cando a altura do líquido é a mesma nas dúas zonas. A superficie do líquido será horizontal.

Algunhas aplicacións
Os vasos comunicantes
- Se temos varios recipientes cun líquido e están conectados de xeito que o líquido poida pasar duns aos outros, o nivel do líquido estará na mesma liña horizontal en todos eles.
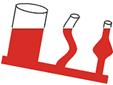
O sifón
- Son dous vasos comunicantes pero que están conectados mediante un tubo que vai por riba da superficie. Serve para pasar o líquido dun recipiente superior a outro inferior sen ter que inclinar o primeiro. Entanto que o tubo en teña líquido caerá auga do vaso superior ao inferior. Así é como podemos sacar gasolina do depósito dun coche (sen inclinar o coche!), ou baleirar un depósito automaticamente cando o líquido chega a un determinado nivel.

O nivel
- Un tubo de plástico longo e transparente con auga pode servir como un nivel barato para trazar liñas horizontais nun terreo.

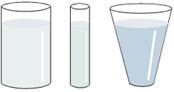
A forma do recipiente que conteña o líquido e a cantidade de líquido non inflúen no valor da presión exercida polo líquido: só importan a densidade e a profundidade. Faga a experiencia resolvendo a actividade proposta S14.
Actividade resolta
A densidade da auga do mar é aproximadamente 1 030 kg/m3. Calcule a presión que soporta un submarino que está a unha profundidade de 150 m.
Solución
Actividades propostas
S14. Colla diferentes recipientes, botellas, tubos, etc., que teñan formas e anchuras diferentes. Bótelles auga ata a mesta altura. Comprobe que no fondo de todos eles hai a mesma presión.
 |
Exemplo: canta presión hai no fondo dun depósito de auga (densidade 1000 kg/m3) que ten unha altura de 20 m? |
S15. O submarino do que falamos na actividade resolta ten unha porta de 1,20 m2. Canta forza fai a presión do mar sobre ela? Sería capaz de abrila desde o interior do buque?
S16. Os mergulladores saben que cada 10 m que afondan no mar a presión aumenta nunha atmosfera aproximadamente. Compróbeo facendo o cálculo. Como conseguen que a presión da auga non esmague o seu corpo?
S17. Canta presión haberá no fondo dun depósito de auga se o levamos moi lonxe da Terra de xeito que o campo gravitacional sexa case nulo?
S18. Un tubo está cheo de mercurio líquido (densidade = 13,6 g/cm3). Ten unha altura de 76 cm.
- Pase a densidade do mercurio a unidades do SI.
- Calcule a presión que exerce o mercurio no fondo do tubo.
- Demostre que unha columna de 1 mm de Hg (mercurio) exerce unha presión de 133 Pa. Logo revise a táboa de equivalencias de unidades de presión en páxinas anteriores.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0