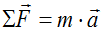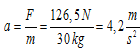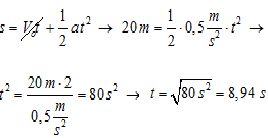2.1.2 Segunda lei da dinámica de Newton: lei fundamental

Nas experiencias co carriño antes vistas concluímos que cando a forza que actúa sobre un corpo non é nula o corpo se move con aceleración e, ademais, esta aceleración é directamente proporcional á forza e inversamente proporcional á masa do corpo:

Despexando a forza, podemos reescribir esta ecuación así: 

Segunda lei da dinámica de Newton

A forza resultante (suma de forzas) que se exerce sobre un corpo é igual á súa masa multiplicada pola aceleración con que se move.

Fíxese en que a aceleración nun corpo é consecuencia da forza total resultante sobre el, e non de cada forza por separado; e que tanto a forza como a aceleración son vectores: a aceleración do corpo terá a mesma dirección e o mesmo sentido que a forza resultante.

A unidade de forza: o newton

Agora xa podemos comprender o que significa o newton, a unidade de forza. Imaxine que ten un corpo de 1 kg de masa e quere que avance cunha aceleración de 1 m/s². Canta forza ten que facer sobre el? Pois exactamente 1 N, xa que:

Daquela:

 Actividades resoltas

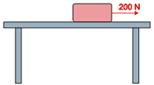
Sobre o bloque da figura, de 30 kg, facemos unha forza de 200 N. Calculemos a aceleración con que se moverá. O coeficiente de rozamento entre o corpo e a mesa é 0,24.

Solución

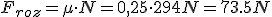
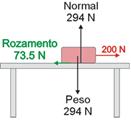
Hai catro forzas sobre o corpo, a de 200 N que facemos nós, o peso, a normal e o rozamento. Calculemos o valor delas:     Peso = m.g = 30 kg. 9,8 N/kg = 294 N     Normal = peso = 294 N [peso e normal son iguais ao estar o corpo en repouso, e as verticais teñen que sumar cero].     Forza de rozamento:      Vemos debuxadas todas as forzas sobre o corpo na figura seguinte.     Temos que calcular a suma de forzas. 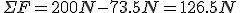A normal máis o peso anúlanse, e a forza resultante é:       Esta forza resultante tira do corpo cara á dereita; finalmente, a aceleración é:     O bloque avanzará cunha aceleración de 4,2 m/s2 mentres se faga forza sobre el.

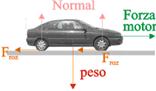
Un coche de 1 000 kg avanza por unha estrada horizontal con velocidade constante de 50 km/h. Se o coeficiente de rozamento entre os pneumáticos e o asfalto é 0,40, calcule:

• O valor da forza normal en cada roda.
• O valor total da forza de rozamento.
• Cantos newtons de forza está a facer o motor nese intre?

Solución

Peso do coche = m.g = 1000 kg . 9,8 N/kg = 9800 N     Como o coche non se move nin cara arriba nin cara a abaixo, a suma das forzas verticais ten que dar cero; por tanto o peso ten que valer igual que a forza normal: N = peso = 9800 N     A forza de rozamento da estrada contra o coche vale:   Froz = .N = 0,40 . 9800 N = 3920 N. Daquela: Forza normal en cada roda: 9800/4 = 2450 N Forza total de rozamento: 3920 N Forza que fai o motor. O coche avanza con velocidade constante, así que a suma das forzas horizontais sobre el ten que valer cero: o motor ten que compensar o rozamento, Fmotor = Froz = 3920 N

Un guindastre está subindo, mediante un cable, unha peza de ferro de 300 kg de masa cunha pequena aceleración de 0,5 m/s². Calcule:

• O peso da peza de ferro.
• A forza total que hai sobre a peza.
• Canto tempo tardará o guindastre en subir a peza a unha altura de 20 m?

Solución

O bloque de ferro sobe con aceleración. Peso da peza = m.g = 300 kg. 9,8 N/kg = 2940 N A forza total é a suma vectorial da tensión máis o peso, pero aínda non sabemos canto vale a tensión do cable; así que usamos outra estratexia: aplicamos a segunda lei de Newton: Ftotal = m.a → Ftotal = 300 kg. 0,5 m/s2 = 150 N. A forza total é 150 N cara arriba. Daquela, T – mg = 150 N → T = mg + 150 N = 2940 N +150 N = 3090 N [observe que o peso pómolo negativo porque é un vector de sentido contrario ao movemento do corpo] Usamos as ecuacións do movemento uniformemente acelerado:

Para que un foguete de 6 000 kg engale verticalmente ten que ter unha aceleración de 12 m/s². Supóndomos desprezable o rozamento contra o aire, calcule canta forza teñen que facer os motores do foguete no lanzamento.

Solución

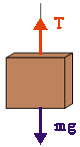
As forzas que actúan sobre o foguete son o pulo dos motores cara a arriba e o peso cara a abaixo. A forza dos motores é positiva porque favorece o movemento do foguete, e o peso é negativo porque vai en sentido contrario ao movemento. Aplicamos a segunda lei de Newton, e

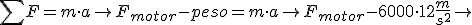
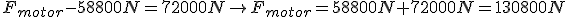
Actividade proposta

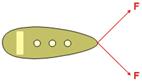
S3. Un buque petroleiro de 2.10⁶ kg é levado a porto por dous remolcadores; cada un deles tira cunha forza de 10 000 N. O ángulo entre os cables de arrastre é de 90º, e a forza de rozamento do petroleiro contra a auga do mar é de 7 000 N.

Debuxe a forza resultante sobre o petroleiro e ache o seu módulo Determine a aceleración coa que avanza o buque. Se inicialmente estaba en repouso, canto tempo tarda en ter unha velocidade de 2 m/s? Canto tardará en percorrer os 950 m que lle faltan para chegar ao peirao?