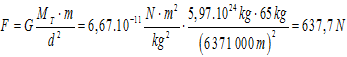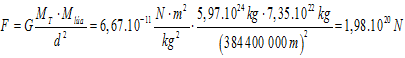2.2 Lei da gravitación universal

As pedras caen ao chan, a Lúa dá voltas arredor da Terra (non se move en liña recta, así que ten que haber algunha forza que curve a súa traxectoria), no mar hai mareas, etc. Todo isto e mais as leis de Kepler fixéronlle pensar a Newton cal podía ser a causa. E chegou a unha conclusión, que coñecemos co nome de lei da gravitación universal.

Newton pensou que a causa común dos feitos anteriores era que todos os corpos se atraen entre si simplemente por teren masa. A Terra atrae a pedra, e por iso cae; tamén atrae a Lúa, por iso dá voltas arredor de nós; a Lúa atrae a auga dos mares, co que a levanta e ocasiona deste xeito as mareas. Newton comparou a aceleración con que caen os corpos (a lenda di que foi unha mazá) e a aceleración con que se move a Lúa, e enunciou a súa lei:

Lei da gravitación universal

A forza gravitacional coa que se atraen mutuamente dous corpos calquera é directamente proporcional ás masas deles e inversamente proporcional ao cadrado da distancia entre eles. Isto resúmese na fórmula da dereita:

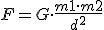
Na fórmula anterior, G é a constante da gravitación universal, que foi medida experimentalmente, e resultou ter un valor:

Na fórmula anterior m₁e m₂son as masas dos corpos e d é a distancia entre os centros eles. Como o valor da constante G é moi pequeno, as forzas gravitacionais son moi pequenas, agás que os corpos teñan moita masa. Así, a forza de atracción entre dúas persoas de 70 kg separadas 20 cm é nada máis que oito millonésimas de newton, por iso non a notamos.

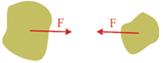
Observe que as dúas forzas de atracción entre os corpos son iguais: non é certo que o corpo grande atraia con máis forza o pequeno do que o pequeno atrae o grande; a atracción é consecuencia da interacción entre os dous simultaneamente; cumpren a terceira lei da dinámica. As dúas forzas teñen o mesmo módulo.

O peso, xa estudado na unidade didáctica anterior, é a forza gravitacional entre o planeta Terra e os corpos que hai arredor dela, e tamén pode calcularse coa fórmula anterior. O peso dun corpo diminúe á medida que se vai arredando da Terra. No cumio dun monte elevado pesamos lixeiramente menos, porque estamos máis lonxe do centro da Terra.

A lei da gravitación permite explicar correctamente os movementos dos astros, como os planetas, satélites e cometas arredor do Sol. Newton veu demostrar así que a materia celeste se comporta de igual xeito que a da Terra. A aplicación das leis de Newton permitiu localizar e descubrir ao planeta Neptuno e tamén a Plutón.

Actividades resoltas

Calcule a forza gravitacional de atracción entre a Terra e un home de 65 kg situado na súa superficie [masa da Terra = 5,97.10²⁴ kg; raio da Terra = 6 371 km].

Solución

Fíxese que a distancia haina que medir entre o centro da Terra e o centro da persoa, o que vén sendo o radio da Terra aproximadamente; ademais hai que pór esa distancia en metros, non en quilómetros.

Calcule a forza de atracción entre a Terra e a Lúa [masa da Lúa: 7,35.10²² kg; distancia entre centro da Lúa e o centro da Terra: 384 400 km].

Solución