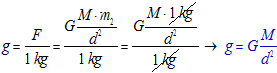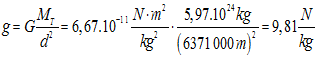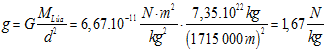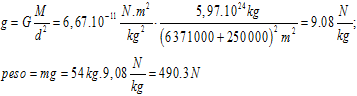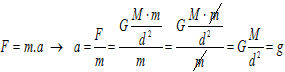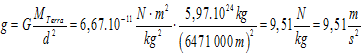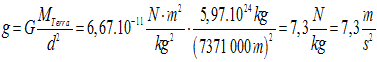2.2.1 Campo gravitacional. Aceleración da gravidade
- Campo gravitacional. Xa sabemos que a Terra atrae todos os corpos que están arredor dela. Chámaselle campo gravitacional (g) á forza con que a Terra atrae cada kg de masa.
- Podemos calcular o valor do campo gravitacional g usando a lei da gravitación.
Nesa fórmula, M é a masa da Terra e d a distancia ao centro terrestre. O campo gravitacional mídese en N/kg ou en m/s2. É un vector que sempre apunta cara ao centro da Terra. Observe que o valor do campo gravitacional diminúe coa distancia a Terra. Canto máis lonxe da Terra esteamos, menor ha ser intensidade coa que o planeta atrae aos corpos.
Actividades resoltas
Calcule o valor do campo gravitacional na superficie da Terra [masa da Terra = 5,97.1024 kg; raio da Terra = 6 371 km].
Solución
i
Xa ve que o valor do campo gravitacional na superficie da Terra, que é onde vivimos, é o coñecido 9,8 que tanto temos usado. Obviamente, na superficie da Lúa ou doutros planetas non valerá o mesmo.
Calcule o valor da gravidade na superficie lunar [masa da Lúa 7,35.1022 kg; raio da Lúa: 1 715 km].
Solución
i
Xa dixemos que o valor do campo gravitacional diminúe co cadrado da distancia: se nos imos arredando da Terra, a gravidade ha valer cada vez menos. Compróbeo na actividade proposta S9
Calcule o seu peso (54 kg) se está:
- No polo norte.
- A 250 km de altura sobre o planeta.
Solución
- No polo norte, g = 9,83N/kg. Daquela, peso = m.g = 54 kg. 9,83 N/kg = 530,8 N.
- A 250 km de altura:
i
Se nun campo gravitacional deixamos un corpo en liberdade, o corpo caerá cara ao centro do planeta cunha aceleración igual ao valor de g; isto dedúcese da segunda lei da dinámica. No campo gravitacional, a única forza que hai sobre o corpo é a gravitacional, así que a aceleración do corpo valerá:
Usando os resultados de actividades anteriores, diga con que aceleración caerá un corpo que se deixe libre:
- A 100 km de altura sobre a superficie da Terra.
- A 1 000 km de altura.
Solución
- Temos que calcular o valor da gravidade (g) a 100 km de altura sobre a superficie; daquela a distancia ao centro da Terra é 6371 km + 100 km = 6471 km = 6471 000 m.
Así, se deixamos un corpo en liberdade a 100 km de altura caerá cunha aceleración de 9,51 m/s2.
Xa ve que máis lonxe da Terra os corpos caen cunha aceleración menor.
i
Observe tamén que na fórmula da aceleración da gravidade, g = G.M/d2, non aparece a masa m do corpo que cae (só aparece a do planeta M); por iso todos os corpos caen coa mesma aceleración, independentemente da súa masa, como comprobara Galileo deixando caer diferentes pedras desde o alto da torre de Pisa.
Actividades propostas
S9. Calcule o valor do campo gravitacional:
- A 100 km de altura sobre a superficie da Terra.
- A 1 000 km de altura.
|
i |
Mesmo na superficie da Terra, a gravidade (o campo gravitacional) non vale o mesmo en todos os puntos. Debido a que a Terra non é redonda (esférica) e ao movemento de rotación, a gravidade é un pouco maior nos polos (9,83 N/kg) e menor no ecuador (9,78 N/kg). Unha persoa que fose do ecuador ao polo iría gañando peso, aínda tendo a mesma masa! Unha cuestión: podemos seguir usando a fórmula p = m.g para calcular o peso dun corpo, sabéndomos que g non vale sempre o mesmo? Si podemos, pero usando o valor correcto de g no punto onde estea o corpo. |
S10. Imaxine que vai nunha viaxe espacial e que está xusto á metade de camiño entre a Terra e a Lúa. Canto vale a gravidade (g) nese punto? Colla os datos das masas da Terra e da Lúa das actividades anteriores; a distancia entre Terra e Lúa é de 384 400 km. (Teña en conta que g é un vector, e hai que sumar os campos gravitacionais terrestre e lunar como vectores).
i
No ano 1915 Einstein publicou unha nova teoría sobre a gravitación, dentro da súa teoría xeral da relatividade, na que considera que a gravitación é consecuencia da curvatura do espazo-tempo provocada polos corpos. Malia isto, as ecuacións de Newton seguen a utilizarse moito para calcular as traxectorias dos corpos celestes, con resultados bos. Só cando se trata de buscar resultados moi precisos son necesarias as ecuacións de Einstein.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0