2.3.4 Movimiento rectilíneo uniforme (MRU)

É o movemento máis sinxelo. Un movemento é rectilíneo se a súa traxectoria é unha recta, e é uniforme cando a súa velocidade é sempre a mesma, non varia durante o traxecto.

No movemento uniforme a velocidade media e a velocidade instantánea teñen o mesmo valor, porque se recorren espazos iguais en tempos iguais, así que:

Esta é a ecuación do movemento rectilíneo uniforme.

Xeralmente o tempo inicial t₀ é nulo polo que t₀= 0 e a fórmula queda:

Se queremos calcular o espazo despexamos s da fórmula anterior: s Esta fórmula permite calcular as posicións do móbil en calquera momento. Se non se indica nada en contra, pódese supor que no instante inicial (t = 0) a posición inicial é cero (s_o = 0) polo que a ecuación para calcular a velocidade nun momento dado quedaría aínda máis sinxela:

Exemplo 1. Un ciclista pasa pola posición s₁ = 100 m cando t = 0 s, e pola posición s₂ = 300 m cando t = 22 s. Supoñendo que vai sempre coa mesma velocidade, calcule o seu valor e o instante no que pasará pola posición s = 1.000 m.

Solución:

– Calculamos a súa velocidade:

– Calculamos o instante en que pasará pola posición s = 1.000 m:

Collemos como posición inicial a posición s₁=100 m

Despexando da ecuación o tempo t:

Exemplo 2. Un avión voa a 900 km/h. Canto tarda en percorrer 1.500 km? Solución:

Empregamos a fórmula s = s_o+ v t . Como s_o = 0  s = v.t

Despexamos o tempo e calculamos:

Gráfica posición/tempo dun MRU

Esta gráfica permite visualizar rapidamente moitas das características deste tipo de movemento. Vemos como se fai cuns exemplos:

Exemplo 1. Un móbil está no instante inicial na posición 100 m. Móvese cunha velocidade uniforme de 20 m/s. Debuxe a súa gráfica posición/tempo (gráfica s/t).

Solución: escribimos primeiro a ecuación do movemento e a continuación a táboa de datos s/t, dámoslle valores ao tempo e calculamos s.

s = s_o+ v.t → s = 100 + 20.t

Tempo (s)	0 s	1 s	2 s	4 s	7 s
Posición (m)	100 m	120 m	140 m	180 m	240 m

Observamos que a gráfica resulta ser unha liña recta inclinada: é unha función lineal.

Canto maior sexa a velocidade do móbil, máis inclinada é a liña recta da gráfica. Fíxese no exemplo seguinte:

Exemplo 2. Un móbil A parte da posición inicial s_o = 100 m, e móvese a 20 m/s; outro móbil B parte da orixe (s_o = 0) e leva unha velocidade constante de 40 m/s. Construímos a gráfica s/t de ambos os corpos nos mesmos eixes de coordenadas.

Solución. Facemos as táboas de datos posición/tempo dos dous móbiles:

– Móbil A. Ecuación do movemento: s = 100 + 20.t

Tempo (s)	0 s	2 s	4 s	5 s	6 s
Posición (m)	100 m	140 m	180 m	200 m	220 m

– Móbil B. Ecuación do movemento: s = 0 + 40.t

Tempo (s)	0 s	2 s	4 s	5 s	6 s
Posición (m)	0	80 m	160 m	200 m	240 m

Representamos agora graficamente os dous conxuntos de datos:

Observacións sobre a gráfica e os movementos representados:

a) A liña recta vermella corresponde ao móbil con maior velocidade.
b) O punto de corte das dúas rectas indícanos a posición e o tempo en que B alcanza a A.
c) O móbil B sae desde a orixe perseguindo o móbil A, que sae desde a posición 100 m; despois dos 5 s, B vai por diante de A.

Compartida por galazia LicenzaCC-BY-SA, GeoGebra Terms of Use

Nan flechita da esquina inferior da esquerda de clic para continuar coa animación.
En reset para limpar os datos iniciales.
Mova o punto A para cambiar a distancia inicial.

Actividade resolta

Pomos o cronómetro en marcha cando pasamos por diante da posición 30 m. Camiñamos a unha velocidade constante de 1.1 m/s. Calcule e encha os ocos na táboa de datos posición/tempo seguinte:

Posición	30 m				52 m
Tempo	0 s	1 s	2 s	8 s

Como di que camiña a unha velocidade constante, é un MRU, polo que aplicamos a ecuación 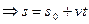. Con s₀= 0 a ecuación queda s = v.t

Substituímos os distintos valores do tempo:

Para t=1 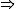s = v.t = 1,1·1 = 1,1 m
Para t=2 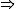s = v.t = 1,1·2 = 2,2 m
Para t=3 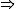s= v.t = 1,1·8 = 8,8 m

Para calcular o tempo no último cadriño despexamos o tempo da ecuación s = v.t:

t = s/v = 52/1,1 = 47,3 s.

Completamos agora a táboa anterior:

Posición	30 m	1,1	2,2	8,8	52 m
Tempo	0 s	1 s	2 s	8 s	47,3

Actividades propostas

S23. Camiñamos de xeito que nunha hora avanzamos 4 km. Supondo velocidade constante, calcule:

a) A velocidade.
b) O tempo que tardamos en percorrer 10 km.
c) O espazo que percorremos en tres horas e media.

S24. A luz e as demais ondas electromagnéticas móvense polo aire e polo baleiro a 300.000 km/s. Se os satélites de televisión están a 36.000 km de altura sobre a Terra,

a) Canto tempo tarda o sinal en ir desde a emisora de TV ata o satélite?
b) Canto tempo tarda en ir o sinal desde a emisora ata a antena da súa casa?

S25. O eco prodúcese cando un son rebota contra unha parede, unha montaña, etc. e volve a nós. Escoitamos o noso eco 3 s máis tarde de dar un forte berro. A que distancia estamos da parede montañosa? Velocidade do son =340 m/s.

S26. Faga a gráfica s/t dun coche que no instante inicial estaba no punto quilométrico 30 km da ruta Ourense-Lugo e se move con velocidade constante de 60 km/h.