2.1.5 Xeometría

Perímetros e áreas

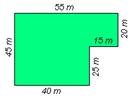
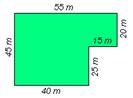
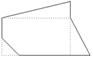
• Perímetros. Supoñamos que queremos pechar un terreo con forma de polígono das dimensións indicadas na figura, cun fío de arame que o rodee perimetralmente. Cantos metros de arame cumprirán para o pechar

Para responder a esta pregunta deberemos sumar as medidas de todos os lados:

55 m + 45 m + 40 m + 25 m + 15 m + 20 m = 200 m

Cumprirían 200 m de arame. Esta medida é o perímetro do terreo. O perímetro dun polígono é a suma das lonxitudes dos lados e exprésase en unidades de lonxitude.

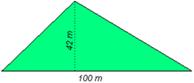
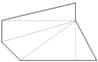
• Áreas. Supoñamos agora que queremos comparar a extensión do terreo anterior con outro terreo de forma triangular, das dimensións indicadas na figura. Cal terá maior extensión?

Neste caso deberemos calcular a área de cada un dos terreos. A área dunha figura é a medida da súa superficie e exprésase en unidades de superficie.

Medir unha superficie consiste en establecer unha unidade de medida e determinar cantas veces está contida a unidade na figura.

A medida da superficie pódese realizar de xeito directo, contando o número de veces que está contida a unidade na figura que estamos a medir, ou de xeito indirecto, por medio de fórmulas matemáticas.

Vexamos como se pode medir directamente a área das seguintes figuras, tomando o cadrado A como unidade de medida. Para saber a súa área é preciso comprobar cantas veces cabe o cadrado unidade en cada unha. Observe que en cada figura podemos unir varias partes menores que a unidade para formar unha unidade completa.

Como pode comprobar, as áreas respectivas das figuras son, por orde, 12 unidades, 12 unidades, 6,5 unidades e 11 unidades

Áreas de polígonos

Medir a área dunha figura de xeito directo resulta difícil cando non podemos formar unidades enteiras coas partes da unidade. Nese caso é mellor efectuar a medición de xeito indirecto, utilizando fórmulas matemáticas. Vexamos como podemos calcular a área das principais figuras por este procedemento.

• Área do rectángulo. Observe que para calcular a área do rectángulo tomando o cadro como unidade de área, podémolo considerar dividido en catro columnas de tres cadros cada unha. Xa que logo, a área do rectángulo será: 4 x 3 cadros = 12 cadros.

Se tomamos o lado do cadro como unidade de lonxitude e designamos as medidas do rectángulo como base (b) e altura (a), a fórmula da área do rectángulo será o produto da base pola altura, ambas expresadas nas mesmas unidades: 

A rectángulo = b x a [Área do rectángulo = Base x Altura]

Sabendo a fórmula da área do rectángulo é doado deducirmos as dos outros polígonos.

• Área do cadrado. Calquera cadrado de lado l pode ser considerado como un rectángulo coa base igual que a altura.

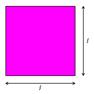
		A cadrado = l x l = l2
		Área do cadrado = Lado x Lado

• Área do triángulo. Vexa o seguinte triángulo. Se o inscribimos nun rectángulo coa mesma base e altura, observe que a área do rectángulo é a metade da do rectángulo.

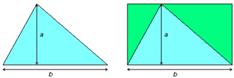
		Atriángulo=
		Área do triángulo = (Base x Altura) / 2

• Área do romboide. Se observa o seguinte romboide ha ver que a súa área é o dobre da área do triángulo coa mesma base e a mesma altura. 

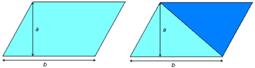
		A romboide = b x a
		Área do romboide = [(Base x Altura) / 2] x 2 = Base x Altura

• Área do rombo. As dimensións características do rombo son, ademais do lado, as diagonais, chamadas diagonal maior (D) e diagonal menor (d). Se inscribimos o rombo nun rectángulo de lados iguais ás diagonais do rombo, podemos ver que a área do rombo é exactamente igual á metade da área do rectángulo.

		Arombo =
		Área do rombo = (Diagonal maior x Diagonal menor) / 2

• Área do trapecio. O trapecio é un cuadrilátero con dous lados paralelos, base maior (B) e base menor (b). Se duplicamos o trapecio e os dispomos como se indica obtemos un romboide de base (B + b) e altura h igual á do trapecio orixinal. Logo a súa área é a metade da área do romboide.

		Atrapecio =
		Área do trapecio = Área do romboide / 2 = (Base x Altura) / 2

• Polígonos regulares. Os polígonos regulares caracterízanse por teren un centro equidistante de cada un dos vértices, polo que é posible descompolos en triángulos iguais de base igual ao lado l do polígono e de altura igual á apotema ap.

A área de cada triángulo:		Polo que a área total é:
Atriángulo=		Atotal=

 Por outra parte, o perímetro do polígono é igual á suma dos seus lados, polo que:

5 x lado = Perímetro (P)

Substituíndo esta igualdade na expresión anterior obtemos a fórmula da área dun polígono regular calquera:

Atotal=

• Figuras compostas. Moitas veces non é posible calcular a área dunha figura porque non se corresponde con ningunha figura elemental das estudadas ata agora. Nese caso cómpre descompola en figuras simples e calcular a área de cada unha por separado. Velaí algúns exemplos de descomposición de figuras complexa en figuras simples:

Outro procedemento consiste en descompor por triangulación a figura dada. Agora a dificultade está en coñecer as medidas de cada triángulo en que se descompón a figura.

Circunferencia e círculo

Vexamos como se calculan a lonxitude da circunferencia e a área do círculo e das figuras circulares.

• Lonxitude da circunferencia. Xa sabe que a circunferencia é unha liña curva, polo que un xeito de medila consiste en rodeala cunha cinta, estendela e medir a lonxitude da cinta. Pero isto é laborioso e moitas veces é imposible de aplicar, polo que é preciso determinar unha fórmula que nos permita determinar a lonxitude mediante o cálculo.

A lonxitude da circunferencia depende do seu diámetro, xa que ambas as magnitudes, lonxitude (L) e diámetro (d) están relacionadas, como é ben sabido desde a antigüidade.

Compartida por FXimeno   Licencia   CC-BY-SA, GeoGebra

 

En todas as circunferencias se cumpre que o cociente entre a lonxitude e a medida do diámetro é, aproximadamente, 3,1416, é dicir, algo máis de tres veces a lonxitude do diámetro. Este número represéntase pola letra grega pi (π).

 

Daquela, a lonxitude de calquera circunferencia pódese calcular multiplicando o diámetro por π.

L = π x d

Tendo en conta que a medida do diámetro é igual ao dobre do raio, podemos expresar a fórmula anterior en función do raio.

L = 2 x π x r

	Ano	Valor de π
Babilonios	Cara a 2000 aC	3 + 1/8
Exipcios	Cara a 2000 aC	256/81
Arquímedes (Gracia)	Cara a 250 aC	Entre 3 + 10/71 e 3 + 10/70
Ptolomeo (Exipto)	150	3,14166
Liu Hui (China)	263	3,14159
Tsu Ch’ung Chi (China)	480	355/113
Aryabhata (India)	499	3,14156
Al-Khowarizmi	800	3,1416
Al-Kashi	1429	3,14159265358979
Vieta (Francia)	1593	3,141592653
Van Ceulen (Holanda)	1615	Valor de π coas primeiras 35 cifras decimais exactas

 

• Lonxitude dun arco de circunferencia. O arco da circunferencia completa mide 360º e a lonxitude dun arco de circunferencia é directamente proporcional ao seu número de graos nº. Daquela, para calcular a súa lonxitude basta resolver a proporción:

 

Desta expresión obtemos a fórmula:

 

• Área do círculo. A área do círculo dedúcese, sabendo que a área interior de calquera polígono regular é igual ao produto do perímetro pola apotema dividido entre 2:

 

Como se pode comprobar na figura, se consideramos a circunferencia como un polígono regular de infinitos lados, o perímetro coincide coa lonxitude da circunferencia (P = 2πr) e a apotema co raio (a_p = r).

Xa que logo, substituíndo na fórmula e simplificando obtemos: 

• Área do sector circular. De igual xeito que razoamos o cálculo da lonxitude dun arco de circunferencia, a área dun sector circular é directamente proporcional ao seu número de graos nº. Por tanto, para calcular a súa área basta resolver a proporción seguinte, da que se obtén a fórmula:

• Área da coroa circular. Para calcular a área dunha coroa circular restámoslle á area do círculo maior, a área do círculo menor.

		Área da coroa circular = π x R2 – π x r2
		Extraendo π factor común, obtemos: A coroa circ. = π x (R2 – r2)

• Área do segmento circular. Para calcular a área do segmento circular restámoslle á área do sector circular, a área do triángulo de base b igual á lonxitude da corda e de altura a, a distancia do centro á corda. 

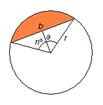
		Área do segmento circular = Área do sector – Área do triángulo

• Área do trapecio circular. O trapecio circular é unha parte da coroa circular polo que, igual que razoamos o cálculo da área do sector circular, a área do trapecio circular é directamente proporcional ao seu número de graos nº. Xa que logo, para calcular a súa área basta resolver a proporción:

Unha ferramenta útil para medir terreos

En internet existen algunhas aplicacións institucionais de acceso libre e gratuíto para medir distancias e superficies sobre mapas e ortofotos de toda España.

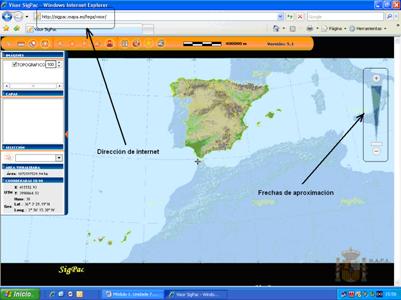
Unha delas áchase no enderezo http://sigpac.mapa.es/fega/visor/ e serve para medir terreos rústicos. Ao acceder atoparemos unha páxina de inicio semellante a esta.

Para situármonos na zona onde queremos facer a medición debemos usar as frechas de aproximación da dereita ou a roda do rato (+ significa “aproximación” e – “afastamento”).

Á medida que nos imos achegando han aparecer sucesivos mapas da superficie e, finalmente, aparecerá a ortofoto do terreo. Para que a medición sexa máis precisa deberemos aproximarnos o máximo posible.

Logo de localizado o terreo sobre o que queremos medir premeremos á esquerda o cadro Parcela para que aparezan en sobreimpresión os límites dos terreos.

Para medir distancias premeremos sobre a icona Medir distancia situada na barra de ferramentas da aplicación. Ao sinalar dous puntos calquera sobre o terreo aparecerá a medida da distancia no recanto inferior esquerdo da pantalla.

Para medir a área premeremos sobre a icona Medir área situada na barra de ferramentas e iremos sinalando sucesivamente os vértices consecutivos da liña poligonal que delimita o terreo. A superficie medida aparecerá resaltada en cor amarela e o resultado da medición no ángulo inferior esquerdo.

Outra aplicación semellante a esta, pero que serve para medir terreos urbanos, é a pertencente á oficina virtual do catastro, situada en https://ovc.catastro.minhac.es/index.asp.

Ao acceder a ela deberemos identificar o terreo mediante a referencia catastral que figura no recibo do imposto de bens inmobles ou polo seu enderezo completo. Na barra de ferramentas existe unha icona para efectuar medicións semellante á anterior.