Glosario
Fricción
-
Definición:
-
Fuerza que se opone al movimiento cuando dos superficies entran en contacto.
-
Ejemplo:
-
Los frenos de la bicicleta funcionan gracias a la fricción entre las pastillas y la rueda.
Pasear sin barreras
Ruedas de fricción
Conoce el mecanismo
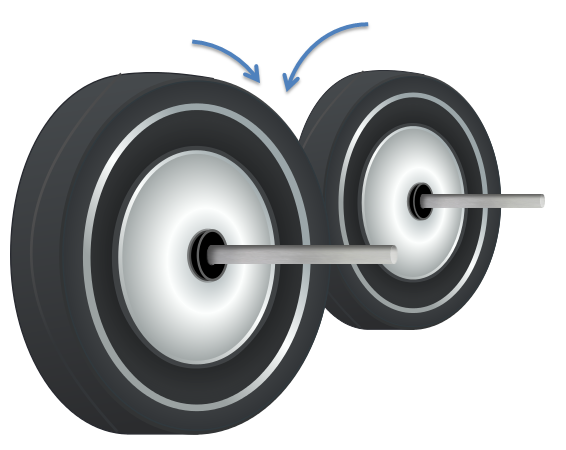Este mecanismo está formado por dos ruedas, situadas una en contacto con la otra. La transmisión del movimiento entre las dos ruedas se produce por fricción entre ellas.
Recordando la anterior definición de mecanismo de transmisión, la rueda que transmite el movimiento se llamamos motriz o conductora y la que es arrastrada la llamamos arrastrada o conducida.
Lectura facilitada
Este mecanismo tiene dos ruedas en contacto directo. El movimiento se transmite por fricción entre ellas.
La rueda que inicia el movimiento se llama motriz o conductora, y la rueda que es movida se llama conducida o arrastrada.
Para saber más: demostración de la ecuación general caso ruedas de fricción
Supongamos dos ruedas de fricción que giran con diferentes velocidades de rotación. Estas ruedas están en contacto en un único punto, y en ese punto comparten la misma velocidad lineal.
\(v = \frac{espacio}{tiempo} \)
Si consideramos un tiempo fijo, el espacio recorrido por ese punto será el mismo, independientemente de la rueda.
Esto significa que podemos calcular el espacio imaginando el punto P girando en la rueda de entrada o en la rueda de salida; el resultado será idéntico.
- Longitud recorrida por cada rueda
-
Imagina dos ruedas en contacto, una es la rueda de entrada (verde) y la otra es la rueda de salida (morada). Cuando ambas giran, el punto de contacto entre las dos ruedas tiene la misma velocidad, es decir, en el mismo tiempo recorre la misma distancia.
La distancia recorrida por el borde de una rueda se calcula con su perímetro, que es:
\[\text{Perímetro} = 2 \cdot \pi \cdot r \]
Para la rueda de entrada: \(\text{Perímetro}_e = 2 \cdot \pi \cdot r_e \)
Para la rueda de salida: \(\text{Perímetro}_s = 2 \cdot \pi \cdot r_s \)
- Espacio recorrido por cada rueda
-
El espacio que recorre cada rueda depende de su perímetro y del número de vueltas que da. Se calcula así:
Espacio = Perímetro · Número de vueltas
Para la rueda de entrada: \( \text{Espacio}_e = 2 \cdot \pi \cdot r_e \cdot n_e \).
Para la rueda de salida: \( \text{Espacio}_s = 2 \cdot \pi \cdot r_s \cdot n_s \)
- Igualdad de espacios recorridos
-
Como ambas ruedas giran juntas, el espacio recorrido por el punto de contacto es el mismo para las dos:
\[\text{Espacio}_e = \text{Espacio}_s \]
Por lo tanto:
\[2 \cdot \pi \cdot r_e \cdot n_e = 2 \cdot \pi \cdot r_s \cdot n_s \]
- Simplificación
-
Podemos simplificar eliminando \(\pi\) en ambos lados:
\[2 \cdot r_e \cdot n_e = 2 \cdot r_s \cdot n_s \]
Como el diámetro (\(d = 2 \cdot r\)), tenemos:
\[d_e \cdot n_e = d_s \cdot n_s \]
Esta relación nos dice que el producto del diámetro de una rueda por su velocidad de giro es el mismo para ambas ruedas.
Empleando esta relación, podemos expresar la relación de transmisión así:
\[ i= \frac{n_s}{n_e} = \frac{d_e}{d_s} \]
Lectura facilitada
Cuando dos ruedas de fricción giran a diferentes velocidades, el punto donde se tocan se mueve a la misma velocidad en ambas.
\(v = \frac{espacio}{tiempo} \)
Si medimos en un mismo tiempo, la distancia recorrida en ese punto será igual para ambas ruedas.
Podemos calcular este espacio considerando el giro en la rueda de entrada o en la de salida, obteniendo el mismo resultado.
- Longitud recorrida por cada rueda
-
Imagina dos ruedas en contacto: la rueda de entrada (verde) y la rueda de salida (morada).
Cuando giran, el punto donde se tocan recorre la misma distancia en ambas ruedas en el mismo tiempo.
La distancia recorrida en el borde de cada rueda se calcula con su perímetro:
\[\text{Perímetro} = 2 \cdot \pi \cdot r \]
Para la rueda de entrada: \(\text{Perímetro}_e = 2 \cdot \pi \cdot r_e \)
Para la rueda de salida: \(\text{Perímetro}_s = 2 \cdot \pi \cdot r_s \)
- Espacio recorrido por cada rueda
-
El espacio que recorre cada rueda depende de su perímetro y del número de vueltas que da. Se calcula así:
Espacio = Perímetro · Número de vueltas
Para la rueda de entrada: \(\text{Espacio}_e = 2 \cdot \pi \cdot r_e \cdot n_e \).
Para la rueda de salida: \(\text{Espacio}_s = 2 \cdot \pi \cdot r_s \cdot n_s \)
- Igualdad de espacios recorridos
-
Como ambas ruedas giran juntas, el espacio recorrido por el punto de contacto es el mismo para las dos:
\[\text{Espacio}_e = \text{Espacio}_s \]
Por lo tanto:
\[ 2 \cdot \pi \cdot r_e \cdot n_e = 2 \cdot \pi \cdot r_s \cdot n_s \]
- Simplificación
-
Podemos simplificar eliminando \(\pi\) en ambos lados:
\[2 \cdot r_e \cdot n_e = 2 \cdot r_s \cdot n_s \]
Como el diámetro se define como \(d = 2 \cdot r \), podemos escribir:
\[d_e \cdot n_e = d_s \cdot n_s \]
Esto significa que el producto del diámetro de una rueda por su velocidad de giro es el mismo para ambas ruedas.
Así, la relación de transmisión se expresa como:
\[i= \frac{n_s}{n_e} = \frac{d_e}{d_s} \]
Ecuación general
Cuando dos ruedas de fricción están en contacto, el punto de contacto entre ambas ruedas se mueve a la misma velocidad por lo que, en un mismo tiempo, recorre igual espacio.
Puedes consultar una demostración más detallada como curiosidad, aunque puede resultar un poco avanzada para este nivel. A partir de ahora, trabajaremos directamente con la expresión:
\[d_e \cdot n_e = d_s \cdot n_s\]
ne = velocidad de giro de la rueda de entrada o motriz (normalmente en rpm).
ns= velocidad de giro de la rueda de salida o conducida (normalmente en rpm).
de= diámetro de la rueda de entrada o motriz.
ds= diámetro de la rueda de salida o conducida.
Relación de transmisión
En este caso, relación de transmisión (i), teniendo en cuenta la expresión general, se calcula del siguiente modo:
\(i = \frac {n_s} {n_e} = \frac {d_e} {d_s} \)
ne = velocidad de giro de la rueda de entrada o motriz (normalmente en rpm).
ns= velocidad de giro de la rueda de salida o conducida (normalmente en rpm).
de= diámetro de la rueda de entrada o motriz.
ds= diámetro de la rueda de salida o conducida.
Por tanto, si la velocidad de la rueda conducida es mayor que la de la rueda conductora, estamos ante un mecanismo multiplicador de la velocidad (y reductor de la "potencia").
Por el contrario, si la velocidad de la rueda conducida es menor que la de la rueda conductora estamos ante un mecanismo reductor de la velocidad (y multiplicador de la "potencia").
Nota. - Observa que las ruedas más pequeñas giran más rápido que las grandes. Y tendrán menos "potencia".
Características
- La rueda conducida gira siempre en sentido contrario a la rueda conductora.
- No transmiten grandes potencias, ya que podrían patinar.
- Se desgastan tras un uso prolongado (la transmisión del movimiento se realiza por fricción).
Aplicaciones
Aplicaciones: cojinetes, norias, tocadiscos, …
Lectura facilitada
Ecuación general
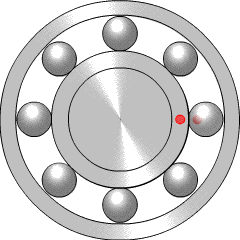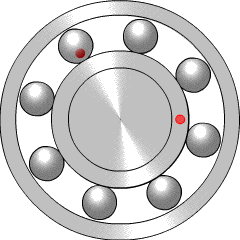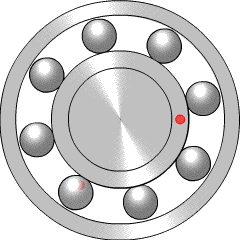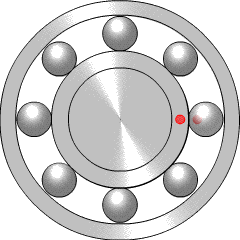
Cuando dos ruedas de fricción están en contacto, el punto donde se tocan se mueve a la misma velocidad.
La relación entre sus diámetros y velocidades es:
\(d_e \cdot n_e = d_s \cdot n_s \)
ne: velocidad de la rueda motriz (rpm).
ns: velocidad de la rueda conducida (rpm).
de: diámetro de la rueda motriz.
ds: diámetro de la rueda conducida.
Relación de transmisión
Se calcula con:
\(i = \frac{n_s}{n_e} = \frac{d_e}{d_s} \)
Si la rueda conducida gira más rápido que la motriz, el mecanismo aumenta la velocidad, pero reduce la potencia.
Si la rueda conducida gira más lento, el mecanismo reduce la velocidad y aumenta la potencia.
Características
- La rueda conducida gira en sentido contrario a la motriz.
- No soporta grandes potencias, porque puede patinar.
- Se desgasta con el uso, ya que funciona por fricción.
Aplicaciones
Se usan en cojinetes, norias y escaleras mecánicas.
Un ejemplo de cálculo
Problema propuesto
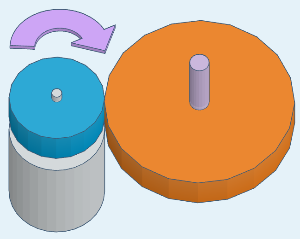En un sistema de ruedas de fricción, hay dos ruedas. La rueda de entrada, también llamada motriz, mide 10 cm de diámetro y está conectada a un motor que gira a 100 vueltas por minuto. La rueda de salida, llamada conducida, mide 20 cm de diámetro.
Preguntas
- ¿Cuál es la relación de trasmisión del sistema?
- ¿A qué velocidad (en rpm) girará la rueda de salida?
- ¿Es este un sistema reductor de velocidad? ¿Por qué?
Solución
- Datos e incógnitas
-
de = 10 cm
ds = 20 cm
ne = 100 rpm
ns = ?
i = ?
- a. Cálculo de la relación de transmisión
-
Para el cálculo de la relación de transmisión se emplea la expresión que ya conoces:
\(i = \frac{d_e}{d_s} = \frac{10 \, \text{cm}}{20 \, \text{cm}} = \frac{1}{2} = 0.5 \)
Esto significa que, por cada vuelta completa de la rueda de entrada, la rueda de salida girará solo la mitad de una vuelta.
- b. Cálculo de la velocidad de la rueda de salida o rueda conducida
-
La velocidad de la rueda de salida se calcula con la expresión de la relación de transmisión en función de las velocidades.
\(i = \frac {n_s} {n_e} \)
\(n_s = n_e \cdot i = 100 \, \text{rpm} \cdot 0.5 = 50 \, \text{rpm} \)
- c. ¿Es un sistema reductor de velocidad?
-
Sí, el sistema reduce la velocidad. La rueda de mayor diámetro gira más despacio que la rueda más pequeña. En este caso, la velocidad en la salida del sistema es más pequeña que la velocidad en su entrada.
Lectura facilitada
Problema propuesto
En un sistema de ruedas de fricción, la rueda de entrada (motriz) tiene un diámetro de 10 cm y gira a 100 rpm. La rueda de salida (conducida) tiene un diámetro de 20 cm.
Preguntas
- ¿Cuál es la relación de transmisión?
- ¿A qué velocidad girará la rueda de salida?
- ¿Este sistema reduce la velocidad? ¿Por qué?
Solución
- Datos:
-
de = 10 cm
ds = 20 cm
ne = 100 rpm
ns = ?
i = ?
- a. Cálculo de la relación de transmisión
-
La relación de transmisión se calcula con:
\(i = \frac{d_e}{d_s} = \frac{10}{20} = 0.5 \)
Esto significa que la rueda de salida gira a la mitad de la velocidad de la rueda de entrada.
- b. Cálculo de la velocidad de la rueda de salida
-
Usamos la ecuación:
\( n_s = n_e \cdot i \)
\( n_s = 100 \cdot 0.5 = 50 \) rpm
- c. ¿Es un sistema reductor de velocidad?
-
Sí, es un sistema reductor. La rueda de salida es más grande y gira más lento que la rueda de entrada.
Plantéate más preguntas
- ¿Qué ocurriría si ambas ruedas tuviesen el mismo diámetro? ¿Cómo afectaría esto a la relación de transmisión y a las velocidades de las ruedas?
- ¿Cómo se modificaría la relación de transmisión si el diámetro de la rueda de salida cambiara de 20 cm a 30 cm?
- ¿Qué pasaría si conectamos el motor a la rueda de mayor tamaño? ¿A qué velocidad giraría la rueda pequeña?
Lectura facilitada
- Si ambas ruedas tienen el mismo diámetro, ¿cómo afectaría esto a la relación de transmisión y a sus velocidades?
- Si el diámetro de la rueda de salida cambia de 20 cm a 30 cm, ¿cómo cambiaría la relación de transmisión?
- Si el motor estuviera conectado a la rueda más grande, ¿a qué velocidad giraría la rueda pequeña?
Practica los cálculos
Realiza algunas actividades para reforzar tus conocimientos sobre ruedas de fricción.
%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%DF%F3%E6%FA%C2%E0%FD%F0%FE%F7%FF%E1%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%F1%FB%FD%FC%E1%B0%A8%B0%AE%E2%AC%C0%F7%F3%FE%FB%E8%F3%B2%F3%FE%F5%E7%FC%F3%E1%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%F7%E1%B2%E2%F3%E0%F3%B2%E0%F7%F4%FD%E0%E8%F3%E0%B2%E6%E7%E1%B2%F1%FD%FC%FD%F1%FB%FF%FB%F7%FC%E6%FD%E1%B2%E1%FD%F0%E0%F7%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%BC%AE%BD%E2%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FD%E2%E6%FB%FD%FC%E1%C0%F3%FF%F6%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%E1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%E6%E0%E7%F7%BE%B0%E6%FB%FF%F7%C1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%A1%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A6%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%A3%A2%A2%BE%B0%FF%FD%F6%F7%D0%FD%F3%E0%F6%B0%A8%F4%F3%FE%E1%F7%BE%B0%E3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%C9%E9%B0%FF%FB%FC%B0%A8%A3%A2%A2%A2%BE%B0%FF%F3%EA%B0%A8%A3%A2%A2%A2%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%FE%F7%F4%E6%A9%CE%B0%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FC%B2%E0%E2%FF%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%F6%F7%FE%B2%F7%FC%F5%E0%F3%FC%F3%F8%F7%B2%E1%FB%B2%FE%FD%E1%B2%F6%FBs%FF%F7%E6%E0%FD%E1%B2%F6%F7%B2%FE%F3%E1%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%EB%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%E1%FD%FC%B2%A6%A2%B2%EB%B2%AA%A2%B2%FF%FF%B2%E0%F7%E1%E2%F7%F1%E6%FB%E4%F3%FF%F7%FC%E6%F7%B2%EB%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%F7%E1%B2%E9%FC%EF%B2%E0%E2%FF%BC%B2%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%BC%AE%BD%E2%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%F1%FD%FE%E1%B2%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%A7%A2%BF%A7%A2%B2%F7%EA%F7%BF%F1%FE%F7%F3%E0%CE%B0%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A3%CE%B0%AC%CE%FC%AE%E2%AC%AE%E1%E6%E0%FD%FC%F5%AC%D6%F3%E6%FD%E1%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B2%A6%A2%B2%FF%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%E1%AE%BD%E1%E7%F0%AC%B2%AF%B2%AA%A2%B2%FF%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%FC%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B2%E9%FC%EF%B2%E0%E2%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%E1%AE%BD%E1%E7%F0%AC%B2%AF%B2%AD%AE%BD%E2%AC%CE%FC%AE%E2%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A0%CE%B0%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%FB%FF%F5%B2%E1%E0%F1%AF%CE%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%E0%E7%F7%F6%F3%E1%F4%E0%FB%F1%F1%FB%FD%FC%CD%F4%FE%F7%F1%FA%F3%BC%E1%E4%F5%CE%B0%B2%F3%FE%E6%AF%CE%B0%DE%F3%B2%FB%FF%F3%F5%F7%FC%B2%FF%E7%F7%E1%E6%E0%F3%B2%F6%FD%E1%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%CE%B0%B2%E5%FB%F6%E6%FA%AF%CE%B0%A6%A2%A3%CE%B0%B2%FA%F7%FB%F5%FA%E6%AF%CE%B0%A0%AA%AB%CE%B0%B2%E6%FB%E6%FE%F7%AF%CE%B0%C0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%BA%F1%C0%D7%D3%F5%F3%FE%BB%CE%B0%B2%BD%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%CE%FC%AE%F6%FB%E4%B2%E1%E6%EB%FE%F7%AF%CE%B0%F6%FB%E1%E2%FE%F3%EB%A8%B2%FC%FD%FC%F7%A9%CE%B0%AC%AE%BD%F6%FB%E4%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%CE%FC%AE%F6%FB%E4%B2%E1%E6%EB%FE%F7%AF%CE%B0%F6%FB%E1%E2%FE%F3%EB%A8%B2%FC%FD%FC%F7%A9%CE%B0%AC%AE%BD%F6%FB%E4%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%CE%FC%AE%F6%FB%E4%B2%E1%E6%EB%FE%F7%AF%CE%B0%F6%FB%E1%E2%FE%F3%EB%A8%B2%FC%FD%FC%F7%A9%CE%B0%AC%AE%BD%F6%FB%E4%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A8%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A3%A0%B8%E9%FC%EF%BD%A0%A6%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%F4%F3%FE%E1%F7%EF%BE%E9%B0%FF%FB%FC%B0%A8%A3%BE%B0%FF%F3%EA%B0%A8%A3%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%F6%FBs%FF%F7%E6%E0%FD%B2%E3%E7%F7%B2%F6%F7%F0%F7%B2%E6%F7%FC%F7%E0%B2%FE%F3%B2%E0%E7%F7%F6%F3%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%E1%FB%B2%FE%F3%B2%E0%E7%F7%F6%F3%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%E6%FB%F7%FC%F7%B2%E7%FC%B2%F6%FBs%FF%F7%E6%E0%FD%B2%F6%F7%B2%A4%A2%B2%FF%FF%B2%EB%B2%E3%E7%F7%E0%F7%FF%FD%E1%B2%E3%E7%F7%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%E1%F7%B2%E0%F7%F6%E7%E8%F1%F3%B2%F6%F7%E1%F6%F7%B2%E9%FC%EF%B2%E0%E2%FF%B2%F3%B2%E9%DC%EF%B2%E0%E2%FF%BC%B4%FC%F0%E1%E2%A9%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%BC%AE%BD%E2%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%F1%FD%FE%E1%B2%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%A7%A2%BF%A7%A2%B2%F7%EA%F7%BF%F1%FE%F7%F3%E0%CE%B0%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A3%CE%B0%AC%CE%FC%AE%E2%AC%AE%E1%E6%E0%FD%FC%F5%AC%D6%F3%E6%FD%E1%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%E1%B2%AF%B2%AD%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B2%A4%A2%B2%FF%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%FC%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B2%E9%FC%EF%B2%E0%E2%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%FC%AE%E1%E7%F0%AC%E1%AE%BD%E1%E7%F0%AC%B2%AF%B2%E9%DC%EF%B2%E0%E2%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A0%CE%B0%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%FB%FF%F5%B2%E1%E0%F1%AF%CE%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%E0%E7%F7%F6%F3%E1%F4%E0%FB%F1%F1%FB%FD%FC%CD%F4%FE%F7%F1%FA%F3%BC%E1%E4%F5%CE%B0%B2%F3%FE%E6%AF%CE%B0%DE%F3%B2%FB%FF%F3%F5%F7%FC%B2%FF%E7%F7%E1%E6%E0%F3%B2%F6%FD%E1%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%CE%B0%B2%E5%FB%F6%E6%FA%AF%CE%B0%A6%A2%A3%CE%B0%B2%FA%F7%FB%F5%FA%E6%AF%CE%B0%A0%AA%AB%CE%B0%B2%E6%FB%E6%FE%F7%AF%CE%B0%C0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%BA%F1%C0%D7%D3%F5%F3%FE%BB%CE%B0%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A8%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A4%A2%B8%E9%FC%EF%BD%E9%DC%EF%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%C9%E9%B0%FC%F3%FF%F7%B0%A8%B0%FC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A1%A2%A2%A2%BE%B2%A4%A2%A2%A2%BE%B2%AB%A2%A2%A2%B0%EF%BE%E9%B0%FC%F3%FF%F7%B0%A8%B0%DC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A3%A2%A2%A2%BE%B2%A3%A7%A2%A2%BE%B2%A1%A2%A2%A2%B0%EF%CF%EF%BE%E9%B0%FF%FB%FC%B0%A8%A3%A2%A2%A2%BE%B0%FF%F3%EA%B0%A8%A3%A2%A2%A2%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%FE%F7%F4%E6%A9%CE%B0%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FC%B2%E0%E2%FF%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%F6%F7%FE%B2%E1%FB%E1%E6%F7%FF%F3%B2%F6%F7%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%E1%FB%B2%FE%F3%E1%B2%E0%E7%F7%F6%F3%E1%B2%FF%FD%E6%E0%FB%E8%B2%EB%B2%F1%FD%FC%F6%E7%F1%FB%F6%F3%B2%E6%FB%F7%FC%F7%FC%B2%A3%A0%A2%B2%EB%B2%A0%A6%A2%B2%FF%FF%B2%F6%F7%B2%F6%FBs%FF%F7%E6%E0%FD%B2%E0%F7%E1%E2%F7%F1%E6%FB%E4%F3%FF%F7%FC%E6%F7%B2%EB%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%F7%E1%B2%E9%DC%EF%B2%E0%E2%FF%BC%B2%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%BC%AE%BD%E2%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%F1%FD%FE%E1%B2%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%A7%A2%BF%A7%A2%B2%F7%EA%F7%BF%F1%FE%F7%F3%E0%CE%B0%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A3%CE%B0%AC%CE%FC%AE%E2%AC%AE%E1%E6%E0%FD%FC%F5%AC%D6%F3%E6%FD%E1%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%E2%AC%CE%FC%AE%E2%AC%FC%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B4%FC%F0%E1%E2%A9%B2%AD%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B2%A3%A0%A2%B2%FF%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%E1%AE%BD%E1%E7%F0%AC%B2%AF%B2%A0%A6%A2%B2%FF%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%FC%AE%E1%E7%F0%AC%E1%AE%BD%E1%E7%F0%AC%B2%AF%B2%E9%DC%EF%B2%E0%E2%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A0%CE%B0%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%FB%FF%F5%B2%E1%E0%F1%AF%CE%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%E0%E7%F7%F6%F3%E1%F4%E0%FB%F1%F1%FB%FD%FC%CD%F4%FE%F7%F1%FA%F3%BC%E1%E4%F5%CE%B0%B2%F3%FE%E6%AF%CE%B0%DE%F3%B2%FB%FF%F3%F5%F7%FC%B2%FF%E7%F7%E1%E6%E0%F3%B2%F6%FD%E1%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%CE%B0%B2%E5%FB%F6%E6%FA%AF%CE%B0%A6%A2%A3%CE%B0%B2%FA%F7%FB%F5%FA%E6%AF%CE%B0%A0%AA%AB%CE%B0%B2%E6%FB%E6%FE%F7%AF%CE%B0%C0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%BA%F1%C0%D7%D3%F5%F3%FE%BB%CE%B0%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A8%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A0%A6%A2%B8%E9%DC%EF%BD%A3%A0%A2%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%C9%E9%B0%FC%F3%FF%F7%B0%A8%B0%DC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A3%A2%A2%BE%B2%A0%A2%A2%BE%B2%A0%A6%A2%BE%B2%A1%A2%A2%BE%B2%A1%A4%A2%B0%EF%CF%EF%BE%E9%B0%FF%FB%FC%B0%A8%A3%BE%B0%FF%F3%EA%B0%A8%A3%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%F6%FBs%FF%F7%E6%E0%FD%B2%E3%E7%F7%B2%F6%F7%F0%F7%B2%E6%F7%FC%F7%E0%B2%FE%F3%B2%E0%E7%F7%F6%F3%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%E1%FB%B2%FE%F3%B2%E0%E7%F7%F6%F3%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%E6%FB%F7%FC%F7%B2%E7%FC%B2%F6%FBs%FF%F7%E6%E0%FD%B2%F6%F7%B2%A3%A0%A2%B2%FF%FF%B2%EB%B2%E3%E7%F7%E0%F7%FF%FD%E1%B2%E3%E7%F7%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%E1%F7%B2%E0%F7%F6%E7%E8%F1%F3%B2%F6%F7%E1%F6%F7%B2%E9%FC%EF%B2%E0%E2%FF%B2%F3%B2%E9%DC%EF%B2%E0%E2%FF%BC%B4%FC%F0%E1%E2%A9%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%BC%AE%BD%E2%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%F1%FD%FE%E1%B2%F7%EA%F7%BF%FE%F3%EB%FD%E7%E6%BF%A0%BF%A7%A2%BF%A7%A2%B2%F7%EA%F7%BF%F1%FE%F7%F3%E0%CE%B0%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A3%CE%B0%AC%CE%FC%AE%E2%AC%AE%E1%E6%E0%FD%FC%F5%AC%D6%F3%E6%FD%E1%AE%BD%E1%E6%E0%FD%FC%F5%AC%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B2%AD%AE%BD%E2%AC%CE%FC%AE%E2%AC%F6%AE%E1%E7%F0%AC%E1%AE%BD%E1%E7%F0%AC%B2%AF%B2%A3%A0%A2%B2%FF%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%FC%AE%E1%E7%F0%AC%F7%AE%BD%E1%E7%F0%AC%B2%AF%B2%E9%FC%EF%B2%E0%E2%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%FC%AE%E1%E7%F0%AC%E1%AE%BD%E1%E7%F0%AC%B2%AF%B2%E9%DC%EF%B2%E0%E2%FF%AE%BD%E2%AC%CE%FC%AE%E2%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%F6%FB%E4%B2%F1%FE%F3%E1%E1%AF%CE%B0%F7%EA%F7%BF%F1%FD%FE%B2%F7%EA%F7%BF%F1%FD%FE%BF%A0%CE%B0%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%FB%FF%F5%B2%E1%E0%F1%AF%CE%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%E0%E7%F7%F6%F3%E1%F4%E0%FB%F1%F1%FB%FD%FC%CD%F4%FE%F7%F1%FA%F3%BC%E1%E4%F5%CE%B0%B2%F3%FE%E6%AF%CE%B0%DE%F3%B2%FB%FF%F3%F5%F7%FC%B2%FF%E7%F7%E1%E6%E0%F3%B2%F6%FD%E1%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%CE%B0%B2%E5%FB%F6%E6%FA%AF%CE%B0%A6%A2%A3%CE%B0%B2%FA%F7%FB%F5%FA%E6%AF%CE%B0%A0%AA%AB%CE%B0%B2%E6%FB%E6%FE%F7%AF%CE%B0%C0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%BA%F1%C0%D7%D3%F5%F3%FE%BB%CE%B0%AC%AE%BD%E2%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%BD%F6%FB%E4%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F4%E0%FB%F1%F1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A8%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A3%A0%A2%B8%E9%DC%EF%BD%E9%FC%EF%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%C9%E9%B0%FC%F3%FF%F7%B0%A8%B0%DC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A1%A2%A2%A2%BE%B2%A1%A4%A2%A2%BE%B2%A6%A2%A2%A2%BE%B2%A6%A7%A2%A2%B0%EF%BE%E9%B0%FC%F3%FF%F7%B0%A8%B0%FC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A4%A2%A2%A2%BE%B2%A4%A6%A2%A2%BE%B2%A5%A0%A2%A2%B0%EF%CF%EF%CF%BE%B0%F4%F7%F7%F6%D0%F3%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%AE%BD%E2%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D4%D0%B0%A8%A3%A2%A2%BE%B0%E1%F1%FD%E0%FF%B0%A8%E9%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A3%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%E6%E0%E7%F7%EF%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%AE%E2%AC%AE%BD%E2%AC%CE%FC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%AE%B3%BF%BF%F3%AF%A3%BF%BF%AC%B0%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A0%BE%B0%F7%E0%E0%FD%E0%D3%F0%E1%FD%FE%E7%E6%F7%B0%A8%A3%BE%B0%F7%E0%E0%FD%E0%C0%F7%FE%F3%E6%FB%E4%F7%B0%A8%A2%BC%AB%AB%BE%B0%F7%E0%E0%FD%E0%C6%EB%E2%F7%B0%A8%A0%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%DB%D6%B0%A8%B0%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A7%A3%A0%A3%AA%A2%A6%A3%BF%A4%A2%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%C0%F7%E2%FE%EB%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%D7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%DD%E4%F7%E0%B0%A8%B03%D4%FB%FC%B2%F6%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%B3%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%CB%FD%E7%DA%F3%E1%B0%A8%B0%C6%FB%F7%FC%F7%B2%B7%A3%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%A0%B2%F4%F3%FE%FE%FD%E1%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%D8%E7%F5%F3%E0%B2%FD%E6%E0%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%DE%FD%FD%F9%FB%FC%F5%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%F7%E1%E6%F3%F0%F3%B2%F0%E7%E1%F1%F3%FC%F6%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F8%E7%F5%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%DE%7F%FF%FB%E6%F7%B2%F6%F7%B2%E6%FB%F7%FF%E2%FD%B2%BA%FF%FF%A8%E1%E1%BB%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DC%E7%FF%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B0%BE%B0%FF%F5%E1%D3%FE%FE%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B03%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B2%FE%F3%E1%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%C6%E0%EB%D3%F5%F3%FB%FC%B0%A8%B0%DC%F7%F1%F7%E1%FB%E6%F3%B2%F3%FE%B2%FF%F7%FC%FD%E1%B2%E7%FC%B2%B7%E1%B7%B2%F6%F7%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%E2%F3%E0%F3%B2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%BC%B2%C4%E7%F7%FE%E4%F3%B2%F3%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%D3%FC%E6%F7%E1%B2%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F1%FD%FF%FB%F7%FC%F1%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%FB%FC%F3%B2%FC%FD%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%D3%FC%E1%E5%F7%E0%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%DB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%DE%F3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%E7%F3%E0%F6%F3%F6%F3%B2%F7%E1%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%E7%F7%F6%F7%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F1%E7%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%C2%E0%F7%E4%FB%FD%E7%E1%B0%A8%B0%D3%FC%E6%F7%E0%FB%FD%E0%B0%BE%B0%FF%E1%F5%DC%F7%EA%E6%B0%A8%B0%C1%FB%F5%E7%FB%F7%FC%E6%F7%B0%BE%B0%FF%E1%F5%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%D1%FD%E0%E0%F7%F1%E6%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D1%FE%FD%E1%F7%B0%A8%B0%D1%F7%E0%E0%F3%E0%B0%BE%B0%FF%E1%F5%DC%FD%E6%D1%FD%E0%E0%F7%F1%E6%B0%A8%B0%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%BC%BC%BC%B2%C0%F7%E1%E2%E7%F7%E1%E6%F3%B2%F1%FD%E0%E0%F7%F1%E6%F3%A8%B0%BE%B0%FF%E1%F5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%C1%FD%FE%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D1%FA%F7%F1%F9%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%DF%B0%A8%B0%DA%F3%E1%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%FD%B2%F7%FE%B2%F8%E7%F7%F5%FD%BC%B2%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F7%E1%B2%B7%E1%BC%B0%BE%B0%FF%E1%F5%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%C0%F7%E6%E0%FD%F3%FE%FB%FF%F7%FC%E6%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%DF%FD%E4%F7%DD%FC%F7%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%D6%E7%E2%FE%FB%F1%F3%E6%F7%D3%FC%E1%E5%F7%E0%B0%A8%B0%DC%FD%B2%E2%E7%F7%F6%F7%E1%B2%F6%F3%E0%B2%E1%FD%FE%E7%F1%FB%FD%FC%F7%E1%B2%E0%F7%E2%F7%E6%FB%F6%F3%E1%B0%BE%B0%FF%E1%F5%C7%FC%F1%FD%FF%E2%FE%F7%E6%F7%F6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%F3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C7%FC%E1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%C2%E0%FD%F0%FE%F7%FF%F3%E1%B2%FF%F3%E6%F7%FFs%E6%FB%F1%FD%E1%B0%EF%EF
Calcula en rpm la velocidad en el eje de salida del engranaje si los diámetros de las ruedas de entrada y de salida son 40 y 80 mm respectivamente y la velocidad en el eje de entrada es {n} rpm. No pongas unidades en la solución.
Datos
de = 40 mm
ds = 80 mm
ne = {n} rpm
ds = ?
Calcula el diámetro que debe tener la rueda de fricción de salida si la rueda de entrada tiene un diámetro de 60 mm y queremos que la velocidad de entrada se reduzca desde {n} rpm a {N} rpm. No pongas unidades en la solución.
Datos
ds = ?
de = 60 mm
ne = {n} rpm
ns = {N} rpm
Calcula en rpm la velocidad en el eje de entrada del sistema de ruedas de fricción si las ruedas motriz y conducida tienen 120 y 240 mm de diámetro respectivamente y la velocidad en el eje de salida es {N} rpm. No pongas unidades en la solución.
Datos
ne = ?
de = 120 mm
ds = 240 mm
ns = {N} rpm
Calcula el diámetro que debe tener la rueda de fricción de entrada si la rueda de salida tiene un diámetro de 120 mm y queremos que la velocidad de entrada se reduzca desde {n} rpm a {N} rpm. No pongas unidades en la solución.
Datos
de = ?
ds = 120 mm
ne = {n} rpm
ns = {N} rpm
Recuerda que en un par de ruedas de fricción siempre se cumple:
\[d_e \cdot n_e = d_s \cdot n_s\]
Recuerda que en un par de ruedas de fricción siempre se cumple:
\[d_e \cdot n_e = d_s \cdot n_s\]
Recuerda que en un par de ruedas de fricción siempre se cumple:
\[d_e \cdot n_e = d_s \cdot n_s\]
Recuerda que en un par de ruedas de fricción siempre se cumple:
\[d_e \cdot n_e = d_s \cdot n_s\]
Su navegador no es compatible con esta herramienta.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0