Saltar la navegación

Poleas de transmisión

 

Glosario

Correa

Correa

Definición:

Banda flexible, normalmente hecha de caucho.

Ejemplo:

La correa de la lavadora conecta el motor con el tambor donde introduces la ropa, para hacerlo girar.

Conoce el mecanismo

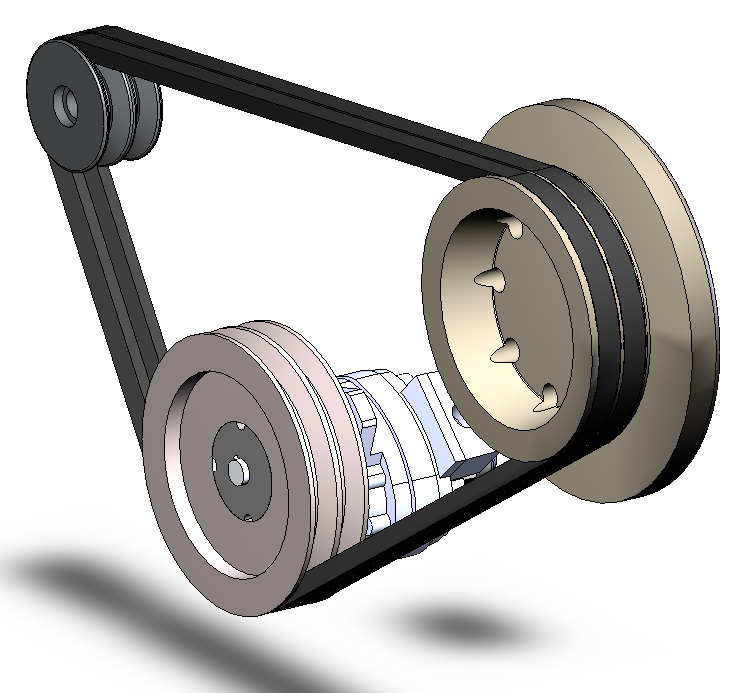Ilustración de un sistema polea correaEste mecanismo está formado por dos o más poleas unidas por una correa. 

Cuando hacemos girar una de las dos poleas, la correa transmite el movimiento y hace que la otra gire.

La polea que transmite el movimiento se llama motriz o conductora. Y la que es arrastrada se llama arrastrada o conducida.

Dicha correa pasa por las acanaladuras que hay en ambas poleas. 

Ecuación general

Dado que el espacio que recorren las dos poleas cuando giran tiene que ser el mismo, se demuestra que:

\[d_e \cdot n_e = d_s \cdot n_s\]

  • ne = velocidad de giro de la polea de entrada o motriz (normalmente en rpm).
  • ns= velocidad de giro de la polea de salida o conducida (normalmente en rpm).
  • de= diámetro de la polea de entrada o motriz.
  • ds= diámetro de la polea de salida o conducida.

Relación de transmisión

En este caso, relación de transmisión (i), teniendo en cuenta la expresión general, se calcula del siguiente modo:

\(i = \frac {n_s} {n_e} = \frac {d_e} {d_s} \)

  • ne = velocidad de giro de la polea de entrada o motriz (normalmente en rpm).
  • ns= velocidad de giro de la polea de salida o conducida (normalmente en rpm).
  • de= diámetro de la polea de entrada o motriz.
  • ds= diámetro de la polea de salida o conducida.

Por tanto, si la velocidad de la polea conducida es mayor que la de la polea conductora, estamos ante un mecanismo multiplicador de la velocidad (y reductor de la "potencia").

Por el contrario, si la velocidad de la polea conducida es menor que la de la rueda conductora estamos ante un mecanismo reductor de la velocidad (y multiplicador de la "potencia").

Nota. - Observa que las poleas más pequeñas giran más rápido que las grandes. Y tendrán menos "potencia".

Características

  • Funcionamiento silencioso.
  • Son baratos
  • Hace posible la transmisión de movimiento circular entre ejes relativamente alejados.
  • No transmiten grandes potencias, ya que puede resbalar la correa. Aunque la transmisión de potencia es mayor que en las ruedas de fricción.

Aplicaciones

  • Electrodomésticos: lavadoras, lavavajillas…
  • Electrónica: lectores de DVD…
  • Automoción: ventilador, alternador, bomba de agua…
Fotografía de correas en automóvil
Correas en automóvil
Fotografía de máquina de coser
Correa de la máquina de coser
Fotografía de correas en telesillas
Correas en telesillas

Lectura facilitada

Sistema polea correa Este mecanismo tiene dos o más poleas conectadas por una correa.

Cuando una polea gira, la correa transmite el movimiento a la otra.

La polea que inicia el movimiento se llama motriz o conductora.

La polea que es arrastrada se llama conducida o arrastrada.

La correa pasa por las ranuras de ambas poleas.

Ecuación general

Las poleas recorren la misma distancia, por lo que se cumple la ecuación:

\( d_e \cdot n_e = d_s \cdot n_s \)

  • ne: Velocidad de la polea motriz (rpm).
  • ns: Velocidad de la polea conducida (rpm).
  • de: Diámetro de la polea motriz.
  • ds: Diámetro de la polea conducida.

Relación de transmisión

Se calcula con la fórmula:

\(i = \frac {n_s} {n_e} = \frac {d_e} {d_s} \)

  • Si la polea conducida gira más rápido que la motriz, el sistema aumenta la velocidad y reduce la potencia.
  • Si la polea conducida gira más lento, el sistema reduce la velocidad y aumenta la potencia.

Nota: Las poleas pequeñas giran más rápido que las grandes y tienen menos potencia.

Características

  • Funcionamiento silencioso.
  • Baratos y fáciles de mantener.
  • Permiten transmitir movimiento entre ejes alejados.
  • Pueden resbalar si la correa no está bien ajustada.

Aplicaciones

  • Electrodomésticos: lavadoras, lavavajillas.
  • Electrónica: lectores de DVD.
  • Automóviles: ventilador, alternador, bomba de agua.
Correas en automóvil
Correas en automóvil
Máquina de coser
Correa en máquina de coser
Correas en telesillas
Correas en telesillas

Un ejemplo de cálculo

Problema propuesto


Poleas de transmisiónEn un motor de un coche se necesita un sistema de poleas para conectar el motor a un ventilador que enfría el sistema. El motor puede girar como máximo a 8000 rpm, pero el ventilador no debe superar las 1000 rpm, para evitar hacer demasiado ruido. 

Preguntas

  1. ¿Cuál es la relación de trasmisión del sistema?
  2. Si la polea conectada al ventilador tiene un diámetro de 10 cm, ¿qué diámetro deberá tener la polea conectada al ventilador?

Solución

Datos e incógnitas

ne = 8000 rpm

ns = 1000 rpm

ds = 5 cm

de = ?

i = ?

a. Cálculo de la relación de transmisión

Para el cálculo de la relación de transmisión se emplea la expresión que ya conoces:

\[
i = \frac{n_e}{n_s} = \frac{8000 \, \text{rpm}}{1000 \, \text{rpm}} = 8
\]

Esto significa que por cada 8 vueltas del motor, el ventilador da 1 vuelta.

b. Cálculo de la velocidad de la rueda de salida o rueda conducida

El diámetro de la rueda del ventilador (rueda de salida) e calcula con la expresión de la relación de transmisión en función de los diámetros.

\(i = \frac {d_e} {d_s} \)

\(d_s = \frac {d_e} {i} =  \frac {5 \, \text{cm}}{0.125} = 40 \, \text{cm} \)

Lectura facilitada

Problema propuesto


Poleas de transmisión En un coche, se necesita un sistema de poleas para conectar el motor a un ventilador. El motor gira a un máximo de 8000 rpm, pero el ventilador no debe superar las 1000 rpm para evitar demasiado ruido.

Preguntas

  1. ¿Cuál es la relación de transmisión?
  2. Si la polea del ventilador mide 10 cm, ¿qué diámetro debe tener la polea del motor?

Solución

Datos:

ne = 8000 rpm

ns = 1000 rpm

ds = 10 cm

de = ?

i = ?

a. Cálculo de la relación de transmisión

La relación de transmisión se calcula con:

\(i = \frac{n_e}{n_s} = \frac{8000}{1000} = 8 \)

Esto significa que por cada 8 vueltas del motor, el ventilador da 1 vuelta.

b. Cálculo del diámetro de la polea del motor

Usamos la ecuación de transmisión en función de los diámetros:

\(i = \frac {d_e} {d_s} \)

\(d_e = d_s \times i = 10 \times 8 = 80 \) cm

La polea del motor debe medir 80 cm de diámetro.

Plantéate más preguntas

  1. ¿Qué pasaría si quisiéramos que el ventilador girara a 2000 rpm como máximo? ¿Cómo cambiaría la relación de transmisión y el diámetro de la polea del ventilador?
  2. Si el ventilador ya tiene una polea de 40 cm de diámetro, ¿qué diámetro debería tener la polea del motor para mantener la relación de transmisión de 1:8?
  3. ¿Qué ventajas tiene usar un sistema de poleas en lugar de las ruedas de fricción?

Lectura facilitada

  1. Si queremos que el ventilador gire a 2000 rpm, ¿cómo cambiaría la relación de transmisión y el diámetro de la polea del motor?
  2. Si el ventilador tiene una polea de 40 cm de diámetro, ¿qué diámetro debería tener la polea del motor para mantener una relación de transmisión de 1:8?
  3. ¿Qué ventajas tiene usar un sistema de poleas en lugar de ruedas de fricción?

Experimenta las poleas de transmisión

En estas simulaciones interactivas puedes experimentar con diferentes diámetros de las poleas de entrada y de salida.

 

Sistema de polea correa directo

En una transmisión directa ambas poleas giran en el mismo sentido. Experimenta con la siguiente aplicación y modifica los diámetros de las poleas de entrada y de salida.

https://www.geogebra.org/m/fazsbmj7 (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/fazsbmj7,Transmisi%F3n%20directa,0,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Persona autora:José Antonio Mora Sánchez

Sistema de polea correa cruzada

En una transmisión cruzada las poleas giran en sentidos contrarios. Experimenta con la siguiente aplicación y modifica los diámetros de las poleas de entrada y de salida.

https://www.geogebra.org/m/gygqanaj (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/gygqanaj,Transmisi%F3n%20inversa,0,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Persona autora:José Antonio Mora Sánchez

Aplica con cálculos

Muy bien. Veo que dominas la fórmula

Resuelve los siguientes problemas de poleas de transmisión

%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%DF%F3%E6%FA%C2%E0%FD%F0%FE%F7%FF%E1%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%F1%FB%FD%FC%E1%B0%A8%B0%AE%E2%AC%C0%F7%E1%E7%F7%FE%E4%F7%B2%FE%FD%E1%B2%E1%FB%F5%E7%FB%F7%FC%E6%F7%E1%B2%E2%E0%FD%F0%FE%F7%FF%F3%E1%B2%F6%F7%B2%E2%FD%FE%F7%F3%E1%B2%F6%F7%B2%E6%E0%F3%FC%E1%FF%FB%E1%FBa%FC%AE%BD%E2%AC%B0%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FD%E2%E6%FB%FD%FC%E1%C0%F3%FF%F6%FD%FC%B0%A8%E6%E0%E7%F7%BE%B0%E1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%E6%E0%E7%F7%BE%B0%E6%FB%FF%F7%C1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%A1%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A6%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%A3%A2%A2%BE%B0%FF%FD%F6%F7%D0%FD%F3%E0%F6%B0%A8%F4%F3%FE%E1%F7%BE%B0%E3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%C9%E9%B0%FF%FB%FC%B0%A8%A3%BE%B0%FF%F3%EA%B0%A8%A3%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FC%B2%E0%E2%FF%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%F6%F7%FE%B2%E1%FB%E1%E6%F7%FF%F3%B2%E1%FB%B2%FE%FD%E1%B2%F6%FBs%FF%F7%E6%E0%FD%E1%B2%F6%F7%B2%FE%F3%E1%B2%E0%E7%F7%F6%F3%E1%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%EB%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%E1%FD%FC%B2%A0%A2%B2%EB%B2%AA%A2%B2%FF%FF%B2%E0%F7%E1%E2%F7%F1%E6%FB%E4%F3%FF%F7%FC%E6%F7%B2%EB%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%F7%E1%B2%E9%FC%EF%B2%E0%E2%FF%BC%B2%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%BC%AE%BD%E2%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E2%FD%FE%F7%F3%E1%B2%F6%F7%B2%E6%E0%F3%FC%E1%FF%FB%E1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A8%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A0%A2%B8%E9%FC%EF%BD%AA%A2%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%C9%E9%B0%FC%F3%FF%F7%B0%A8%B0%FC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A3%A2%A2%A2%BE%B2%A3%A3%A2%A2%BE%A3%A0%A2%A2%BE%A3%A1%A2%A2%BE%A3%A6%A2%A2%BE%A3%A7%A2%A2%BE%A3%A4%A2%A2%BE%A3%A5%A2%A2%BE%A3%AA%A2%A2%BE%A3%AB%A2%A2%BE%B2%A0%A2%A2%A2%BE%A0%A3%A2%A2%BE%A0%A0%A2%A2%BE%A0%A1%A2%A2%BE%A0%A6%A2%A2%BE%A0%A7%A2%A2%BE%A0%A4%A2%A2%BE%A0%A5%A2%A2%BE%A0%AA%A2%A2%BE%A0%AB%A2%A2%BE%A1%A2%A2%A2%BE%A1%A3%A2%A2%BE%A1%A0%A2%A2%BE%A1%A1%A2%A2%BE%A1%A6%A2%A2%BE%A1%A7%A2%A2%BE%A1%A4%A2%A2%BE%A1%A5%A2%A2%BE%A1%AA%A2%A2%BE%A1%AB%A2%A2%BE%A6%A2%A2%A2%B0%EF%CF%EF%BE%E9%B0%FF%FB%FC%B0%A8%A3%BE%B0%FF%F3%EA%B0%A8%A3%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%F6%FBs%FF%F7%E6%E0%FD%B2%E3%E7%F7%B2%F6%F7%F0%F7%B2%E6%F7%FC%F7%E0%B2%FE%F3%B2%E2%FD%FE%F7%F3%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%E1%FB%B2%FE%F3%B2%E2%FD%FE%F7%F3%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%E6%FB%F7%FC%F7%B2%E7%FC%B2%F6%FBs%FF%F7%E6%E0%FD%B2%F6%F7%B2%A0%A2%B2%F1%FF%B2%EB%B2%E3%E7%F7%E0%F7%FF%FD%E1%B2%E3%E7%F7%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%F1%F3%FF%F0%FB%F7%B2%F6%F7%E1%F6%F7%B2%FE%F3%E1%B2%E9%FC%EF%B2%E0%E2%FF%B2%F6%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%F3%B2%FE%F3%E1%B2%E9%DC%EF%B2%E0%E2%FF%B2%F6%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%BC2%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%BC%AE%BD%E2%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E2%FD%FE%F7%F3%E1%B2%F6%F7%B2%E6%E0%F3%FC%E1%FF%FB%E1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A822%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A0%A2%B8%E9%FC%EF%BD%E9%DC%EF%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%C9%E9%B0%FC%F3%FF%F7%B0%A8%B0%FC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A0%A2%A2%BE%B2%A6%A2%A2%BE%B2%A4%A2%A2%BE%B2%AA%A2%A2%BE%B2%A3%A2%A2%A2%BE%B2%A3%A0%A2%A2%BE%A3%A6%A2%A2%BE%B2%A3%A4%A2%A2%BE%B2%A3%AA%A2%A2%BE%B2%A0%A2%A2%A2%B0%EF%BE%E9%B0%FC%F3%FF%F7%B0%A8%B0%DC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A0%A2%A2%BE%B2%A6%A2%A2%BE%B2%A4%A2%A2%BE%B2%AA%A2%A2%BE%B2%A3%A2%A2%A2%BE%B2%A3%A0%A2%A2%BE%A3%A6%A2%A2%BE%B2%A3%A4%A2%A2%BE%B2%A3%AA%A2%A2%BE%B2%A0%A2%A2%A2%B0%EF%CF%EF%BE%E9%B0%FF%FB%FC%B0%A8%A3%BE%B0%FF%F3%EA%B0%A8%A3%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FC%B2%E0%E2%FF%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%F6%F7%FE%B2%E1%FB%E1%E6%F7%FF%F3%B2%F6%F7%B2%E2%FD%FE%F7%F3%E1%B2%E1%FB%B2%FE%F3%E1%B2%E2%FD%FE%F7%F3%E1%B2%FF%FD%E6%E0%FB%E8%B2%EB%B2%F1%FD%FC%F6%E7%F1%FB%F6%F3%B2%E6%FB%F7%FC%F7%FC%B2%A3%A0%B2%EB%B2%A0%A6%B2%F1%FF%B2%F6%F7%B2%F6%FBs%FF%F7%E6%E0%FD%B2%E0%F7%E1%E2%F7%F1%E6%FB%E4%F3%FF%F7%FC%E6%F7%B2%EB%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F7%FC%B2%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%F7%E1%B2%E9%DC%EF%B2%E0%E2%FF%BC%B2%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%AE%BD%E2%AC%CE%FC%AE%E2%AC%AE%BD%E2%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E2%FD%FE%F7%F3%E1%B2%F6%F7%B2%E6%E0%F3%FC%E1%FF%FB%E1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A82%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%CE%FC%AE%E2%AC%AE%BD%E2%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A0%A6%B8%E9%DC%EF%BD%A3%A0%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%C9%E9%B0%FC%F3%FF%F7%B0%A8%B0%DC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A6%A2%BE%B2%A4%A2%BE%B2%AA%A2%BE%B2%A3%A2%A2%BE%B2%A3%A0%A2%BE%B2%A3%A6%A2%BE%B2%A3%A4%A2%BE%B2%A3%AA%A2%BE%B2%A0%A2%A2%BE%B2%A0%A0%A2%BE%B2%A0%A6%A2%BE%B2%A0%A4%A2%BE%B2%A0%AA%A2%BE%B2%A1%A2%A2%BE%B2%A1%A0%A2%BE%B2%A1%A6%A2%BE%B2%A1%A4%A2%BE%B2%A1%AA%A2%BE%B2%A6%A2%A2%BE%B2%A6%A0%A2%BE%B2%A6%A6%A2%BE%B2%A6%A4%A2%BE%B2%A6%AA%A2%BE%B2%A7%A2%A2%BE%B2%A7%A0%A2%BE%B2%A7%A6%A2%BE%B2%A7%A4%A2%BE%B2%A7%AA%A2%BE%B2%A4%A2%A2%BE%B2%A4%A0%A2%BE%B2%A4%A6%A2%BE%B2%A4%A4%A2%BE%B2%A4%AA%A2%BE%B2%A5%A2%A2%BE%B2%A5%A0%A2%BE%B2%A5%A6%A2%BE%B2%A5%A4%A2%BE%B2%A5%AA%A2%BE%B2%AA%A2%A2%BE%B2%AA%A0%A2%BE%B2%AA%A6%A2%BE%B2%AA%A4%A2%BE%B2%AA%AA%A2%BE%B2%AB%A2%A2%BE%B2%AB%A0%A2%BE%B2%AB%A6%A2%BE%B2%AB%A4%A2%BE%B2%AB%AA%A2%BE%B2%A3%A2%A2%A2%B0%EF%CF%EF%BE%E9%B0%FF%FB%FC%B0%A8%A3%BE%B0%FF%F3%EA%B0%A8%A3%A2%BE%B0%F6%F7%F1%FB%FF%F3%FE%E1%B0%A8%A2%BE%B0%E6%FB%FF%F7%B0%A8%A3%AA%A2%BE%B0%F6%F7%F4%FB%FC%F7%F6%C4%F3%E0%FB%F3%F0%FE%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%FB%FC%F5%B0%A8%B0%AE%E2%AC%D1%F3%FE%F1%E7%FE%F3%B2%F7%FE%B2%F6%FBs%FF%F7%E6%E0%FD%B2%E3%E7%F7%B2%F6%F7%F0%F7%B2%E6%F7%FC%F7%E0%B2%FE%F3%B2%E2%FD%FE%F7%F3%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%E1%FB%B2%FE%F3%B2%E2%FD%FE%F7%F3%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%B2%E6%FB%F7%FC%F7%B2%E7%FC%B2%F6%FBs%FF%F7%E6%E0%FD%B2%F6%F7%B2%A3%A2%B2%F1%FF%B2%EB%B2%E3%E7%F7%E0%F7%FF%FD%E1%B2%E3%E7%F7%B2%FE%F3%B2%E4%F7%FE%FD%F1%FB%F6%F3%F6%B2%F1%F3%FF%F0%FB%F7%B2%F6%F7%E1%F6%F7%B2%FE%F3%E1%B2%E9%FC%EF%B2%E0%E2%FF%B2%F6%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%F7%FC%E6%E0%F3%F6%F3%B2%F3%B2%FE%F3%E1%B2%E9%DC%EF%B2%E0%E2%FF%B2%F6%F7%FE%B2%F7%F8%F7%B2%F6%F7%B2%E1%F3%FE%FB%F6%F3%BC2%DC%FD%B2%E2%FD%FC%F5%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FC%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%BC%AE%BD%E2%AC%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%C0%F7%F1%E7%F7%E0%F6%F3%B2%E3%E7%F7%B2%F7%FC%B2%E7%FC%B2%E2%F3%E0%B2%F6%F7%B2%E2%FD%FE%F7%F3%E1%B2%F6%F7%B2%E6%E0%F3%FC%E1%FF%FB%E1%FBa%FC%B2%E1%FB%F7%FF%E2%E0%F7%B2%E1%F7%B2%F1%E7%FF%E2%FE%F7%A82%AE%BD%E2%AC%CE%FC%AE%E2%B2%E1%E6%EB%FE%F7%AF%CE%B0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%A8%B2%F1%F7%FC%E6%F7%E0%A9%CE%B0%AC%AE%E1%E2%F3%FC%B2%E1%E6%EB%FE%F7%AF%CE%B0%F4%FD%FC%E6%BF%E1%FB%E8%F7%A8%B2%A0%A6%E2%E6%A9%CE%B0%AC%CE%CE%C9%F6%CD%F7%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%F7%B2%AF%B2%F6%CD%E1%B2%CE%CE%F1%F6%FD%E6%B2%FC%CD%E1%CE%CE%CF%AE%BD%E1%E2%F3%FC%AC%AE%BD%E2%AC%B0%BE%B0%F4%FD%E0%FF%E7%FE%F3%B0%A8%B0%A3%A2%B8%E9%DC%EF%BD%E9%FC%EF%B0%BE%B0%F6%FD%FF%F3%FB%FC%E1%B0%A8%C9%E9%B0%FC%F3%FF%F7%B0%A8%B0%DC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A3%A2%A2%A2%BE%B2%A3%A7%A2%A2%BE%B2%A0%A2%A2%A2%BE%B2%A0%A7%A2%A2%BE%B2%A1%A2%A2%A2%BE%B2%A1%A7%A2%A2%BE%B2%A6%A2%A2%A2%BE%B2%A6%A7%A2%A2%BE%B2%A7%A2%A2%A2%BE%B2%A7%A7%A2%A2%BE%B2%A4%A2%A2%A2%BE%B2%A4%A7%A2%A2%BE%B2%A5%A2%A2%A2%BE%B2%A5%A7%A2%A2%BE%B2%AA%A2%A2%A2%BE%B2%AA%A7%A2%A2%BE%B2%AB%A2%A2%A2%BE%B2%AB%A7%A2%A2%BE%B2%A3%A2%A2%A2%A2%B0%EF%BE%E9%B0%FC%F3%FF%F7%B0%A8%B0%FC%B0%BE%B0%E4%F3%FE%E7%F7%B0%A8%B0%A3%A2%A2%A2%BE%B2%A0%A2%A2%A2%BE%B2%A6%A2%A2%A2%BE%B2%A7%A2%A2%A2%BE%B2%AA%A2%A2%A2%BE%B2%A3%A2%A2%A2%A2%B0%EF%CF%EF%CF%BE%B0%F4%F7%F7%F6%D0%F3%F1%F9%B0%A8%E6%E0%E7%F7%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%AE%E2%AC%DF%E7%EB%B2%F0%FB%F7%FC%BC%B2%C4%F7%FD%B2%E3%E7%F7%B2%F6%FD%FF%FB%FC%F3%E1%B2%FE%F3%B2%F4a%E0%FF%E7%FE%F3%AE%BD%E2%AC%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D4%D0%B0%A8%A3%A2%A2%BE%B0%E1%F1%FD%E0%FF%B0%A8%E9%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A3%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%E6%E0%E7%F7%EF%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%B0%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A0%BE%B0%F7%E0%E0%FD%E0%D3%F0%E1%FD%FE%E7%E6%F7%B0%A8%A3%BE%B0%F7%E0%E0%FD%E0%C0%F7%FE%F3%E6%FB%E4%F7%B0%A8%A2%BE%B0%F7%E0%E0%FD%E0%C6%EB%E2%F7%B0%A8%A0%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%DB%D6%B0%A8%B0%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A7%A3%A7%A3%A2%A6%A2%A7%A3%BF%A4%A2%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%C0%F7%E2%FE%EB%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%D7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%DD%E4%F7%E0%B0%A8%B03%D4%FB%FC%B2%F6%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%B3%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%CB%FD%E7%DA%F3%E1%B0%A8%B0%C6%FB%F7%FC%F7%B2%B7%A3%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%A0%B2%F4%F3%FE%FE%FD%E1%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%D8%E7%F5%F3%E0%B2%FD%E6%E0%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%DE%FD%FD%F9%FB%FC%F5%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%F7%E1%E6%F3%F0%F3%B2%F0%E7%E1%F1%F3%FC%F6%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F8%E7%F5%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%DE%7F%FF%FB%E6%F7%B2%F6%F7%B2%E6%FB%F7%FF%E2%FD%B2%BA%FF%FF%A8%E1%E1%BB%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DC%E7%FF%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B0%BE%B0%FF%F5%E1%D3%FE%FE%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B03%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B2%FE%F3%E1%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%C6%E0%EB%D3%F5%F3%FB%FC%B0%A8%B0%DC%F7%F1%F7%E1%FB%E6%F3%B2%F3%FE%B2%FF%F7%FC%FD%E1%B2%E7%FC%B2%B7%E1%B7%B2%F6%F7%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%E2%F3%E0%F3%B2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%BC%B2%C4%E7%F7%FE%E4%F3%B2%F3%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%D3%FC%E6%F7%E1%B2%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F1%FD%FF%FB%F7%FC%F1%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%FB%FC%F3%B2%FC%FD%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%D3%FC%E1%E5%F7%E0%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%DB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%DE%F3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%E7%F3%E0%F6%F3%F6%F3%B2%F7%E1%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%E7%F7%F6%F7%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F1%E7%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%C2%E0%F7%E4%FB%FD%E7%E1%B0%A8%B0%D3%FC%E6%F7%E0%FB%FD%E0%B0%BE%B0%FF%E1%F5%DC%F7%EA%E6%B0%A8%B0%C1%FB%F5%E7%FB%F7%FC%E6%F7%B0%BE%B0%FF%E1%F5%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%D1%FD%E0%E0%F7%F1%E6%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D1%FE%FD%E1%F7%B0%A8%B0%D1%F7%E0%E0%F3%E0%B0%BE%B0%FF%E1%F5%DC%FD%E6%D1%FD%E0%E0%F7%F1%E6%B0%A8%B0%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%BC%BC%BC%B2%C0%F7%E1%E2%E7%F7%E1%E6%F3%B2%F1%FD%E0%E0%F7%F1%E6%F3%A8%B0%BE%B0%FF%E1%F5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%C1%FD%FE%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D1%FA%F7%F1%F9%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%DF%B0%A8%B0%DA%F3%E1%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%FD%B2%F7%FE%B2%F8%E7%F7%F5%FD%BC%B2%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F7%E1%B2%B7%E1%BC%B0%BE%B0%FF%E1%F5%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%C0%F7%E6%E0%FD%F3%FE%FB%FF%F7%FC%E6%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%DF%FD%E4%F7%DD%FC%F7%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%D6%E7%E2%FE%FB%F1%F3%E6%F7%D3%FC%E1%E5%F7%E0%B0%A8%B0%DC%FD%B2%E2%E7%F7%F6%F7%E1%B2%F6%F3%E0%B2%E1%FD%FE%E7%F1%FB%FD%FC%F7%E1%B2%E0%F7%E2%F7%E6%FB%F6%F3%E1%B0%BE%B0%FF%E1%F5%C7%FC%F1%FD%FF%E2%FE%F7%E6%F7%F6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%F3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C7%FC%E1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%C2%E0%FD%F0%FE%F7%FF%F3%E1%B2%FF%F3%E6%F7%FFs%E6%FB%F1%FD%E1%B0%EF%EF

Calcula en rpm la velocidad en el eje de salida del sistema si los diámetros de las ruedas de entrada y de salida son 20 y 80 mm respectivamente y la velocidad en el eje de entrada es {n} rpm. No pongas unidades en la solución.

Calcula el diámetro que debe tener la polea de salida si la polea de entrada tiene un diámetro de 20 cm y queremos que la velocidad de entrada cambie desde las {n} rpm del eje de entrada a las {N} rpm del eje de salida. No pongas unidades en la solución.

Calcula en rpm la velocidad en el eje de entrada del sistema de poleas si las poleas motriz y conducida tienen 12 y 24 cm de diámetro respectivamente y la velocidad en el eje de salida es {N} rpm. No pongas unidades en la solución

Calcula el diámetro que debe tener la polea de entrada si la polea de salida tiene un diámetro de 10 cm y queremos que la velocidad cambie desde las {n} rpm del eje de entrada a las {N} rpm del eje de salida. No pongas unidades en la solución.

Recuerda que en un par de poleas de transmisión siempre se cumple:

\[d_e \cdot n_e = d_s \cdot n_s\]

Recuerda que en un par de poleas de transmisión siempre se cumple:  

\[d_e \cdot n_e = d_s \cdot n_s\]

Recuerda que en un par de poleas de transmisión siempre se cumple: 

\[d_e \cdot n_e = d_s \cdot n_s\]

Recuerda que en un par de poleas de transmisión siempre se cumple: 

\[d_e \cdot n_e = d_s \cdot n_s\]

Su navegador no es compatible con esta herramienta.

Creado con eXeLearning (Ventana nueva)