2.3.1 Instalación eléctrica
Antes de analizarmos con detalle os elementos da instalación eléctrica dunha vivenda, veremos algúns conceptos previos: corrente eléctrica, circuítos, magnitudes, etc.
Corrente eléctrica
Cando ao accionarmos un interruptor se acende unha lámpada é porque a través del pasa unha corrente eléctrica. Recibe o nome de corrente eléctrica o movemento ordenado de cargas eléctricas a través dun medio material, por exemplo un fío de cobre, unha disolución de sal en auga, un gas, etc.
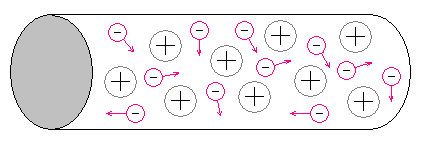
Nos condutores metálicos como os das instalacións domésticas, as cargas en movemento son os electróns (cargas eléctricas negativas), xa que estes se poden desprazar con facilidade entre os átomos. Nas disolucións fórmanse ións positivos e negativos que poden transmitir a corrente eléctrica. Algúns gases, como o vapor de mercurio e o argon, contidos nas lámpadas fluorescentes, ao ionizar, tamén transmiten a corrente eléctrica.
|
|
|
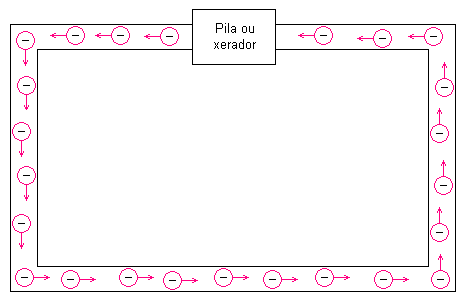
| Nos metais os electróns pódense mover con facilidade entre os átomos | Ao conectarmos o condutor metálico a unha pila ou un xerador eléctrico, os electróns móvense de xeito ordenado e continuo a través del |
As substancias que permiten a circulación das cargas eléctricas a través delas reciben o nome de condutores eléctricos e os que non a permiten, illantes. En xeral, os metais son bos condutores da corrente eléctrica, entanto que os plásticos, a madeira, o vidro ou os materiais cerámicos son illantes. Existen outros materiais denominados semicondutores que en determinadas condicións se poden comportar como condutores ou como illantes. O silicio, o xermanio e o selenio son semicondutores con aplicacións en electricidade e electrónica.
Circuítos eléctricos
Para que os electróns poidan circular precisan unha forza que os impulse. Esta forza prodúcese nun dispositivo chamado xerador, que produce a enerxía eléctrica a partir doutros tipos de enerxía. Así, nas pilas e nas baterías a enerxía eléctrica obtense a partir de reaccións químicas das substancias contidas no seu interior, e na dínamo a partir da enerxía mecánica que a move.
Os aparellos que utilizan a enerxía eléctrica para funcionar chámanse receptores: lámpadas, motores, electrodomésticos, etc. Existen tamén aparellos de medida e interruptores para abrir ou pechar o paso da corrente.
O conxunto de todos estes elementos (xerador, condutores e receptores) recibe o nome de circuíto eléctrico. Para que a corrente circule é preciso que o circuíto estea pechado, é dicir, que desde un extremo a outro do xerador exista sempre un camiño ininterrompido que permita o paso das cargas.
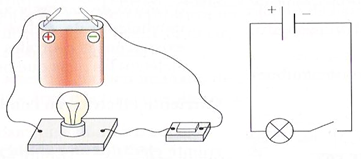
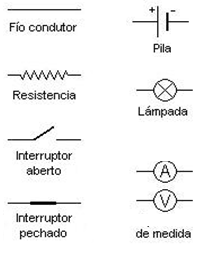
Para simplificar o debuxo os circuítos eléctricos represéntanse utilizando símbolos para cada un dos elementos.
|
|
|
| Circuíto eléctrico | Símbolos utilizados na representación de circuítos eléctricos |
Se conectamos un condutor eléctrico a unha pila, os electróns móvense ao seu través ordenada e continuamente en forma de corrente eléctrica, ata que se consumen os reactivos da pila e esta deixa de producir enerxía. Este tipo de corrente alimentada por pilas ou baterías recibe o nome de corrente continua, xa que os electróns circulan sempre no mesmo sentido a través do condutor, desde o polo negativo da pila ou batería ata o polo positivo.
Non obstante, a corrente doméstica é unha corrente alterna, xa que as cargas se desprazan no condutor alternativamente dun sentido a outro, cambiando de sentido 50 veces por segundo (50 Hz = 50 hertz). Este tipo de corrente é producida nas centrais eléctricas por xeradores eléctricos chamados alternadores .
Existen dous tipo básicos de circuítos eléctricos:
-
En serie. A corrente que pasa por cada un dos elementos conectados é a mesma, xa que os vai atravesando sucesivamente.
-
En paralelo. Os electróns sepáranse ao chegaren á bifurcación, polo que a corrente que pasa polos elementos conectados en paralelo é diferente.
|
|
|
|
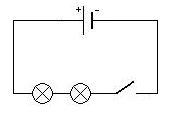
Lámpadas en serie Ao pechar o interruptor ambas as lámpadas se iluminan ao mesmo tempo. |
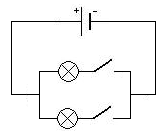
Lámpadas en paralelo Cada unha ten o seu interruptor, e pódese iluminar independentemente unha da outra. |
Magnitudes da corrente eléctrica
Seguidamente defínense as tres magnitudes fundamentais dunha corrente eléctrica.
-
Intensidade. A intensidade (I) de corrente é a cantidade de carga (q) ou número de electróns que atravesan a sección dun condutor nunha unidade de tempo (t). Podémola expresar mediante a fórmula:
I = q / t
A unidade de intensidade no sistema internacional (SI) é o ampere (A). Porén, en moitas ocasións o ampere resulta unha unidade demasiado grande, polo que se utiliza tamén o miliampere (mA), que é a milésima parte do ampere.
1 A = 103 mA 1 mA = 10-3 A
A intensidade de corrente mídese co amperímetro. O amperímetro colócase en serie no circuíto de forma que o atravesen todas as cargas que se queren medir.
-
Diferenza de potencial. Recibe o nome de diferenza de potencial, voltaxe ou tensión (V) entre dous puntos dun circuíto eléctrico a diferenza de enerxía que ten e unidade de carga entre eses dous puntos, e represéntase por V1-V2 ou, abreviadamente, V. A voltaxe entre os polos dunha pila é a enerxía transferida pola pila á unidade de carga eléctrica. Cando se mide nos extremos dun receptor é a enerxía por unidade de carga transformada noutro tipo de enerxía ao pasar polo receptor.
A unidade de voltaxe no SI é o volt (V). O dispositivo que a mide é o voltímetro e conéctase en paralelo entre os dous puntos en que se desexe medir a voltaxe.
|
Pila cilíndrica: 1,5 V Pila de petaca: 4,5 V Corrente doméstica: 220 V Liñas de alta tensión: 20.000 V a 400.000 V |
|
| Exemplos de tensións |
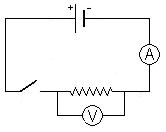
Conexión de aparellos de medida En serie (amperímetro) e en paralelo (voltímetro). |
-
Resistencia. Os átomos dos que están compostos os materiais condutores presentan resistencia ao paso dos electróns. Recibe o nome de resistencia (R) a dificultade que ofrece un condutor ao paso da corrente eléctrica. A resistencia depende de tres factores:
-
Lonxitude (l). Canto máis longo sexa o condutor, maior será a resistencia que encontren os electróns para o atravesar.
-
Sección (s).Canto máis grosor teña o condutor, máis doado circularán os electróns, é dicir, menor será a resistencia. Cómpre ter en conta que o condutor é medio material que permite o paso da corrente e, canto máis groso sexa, máis facilidade teñen os electróns para circularen por el.
-
Natureza do condutor. Non todas as substancias ofrecen a mesma oposición ao paso das cargas eléctricas. A resistividade (ρ) é unha magnitude propia de cada condutor que reflicte a resistencia de cada material: a maior resistividade, máis resistencia eléctrica.
Prata 1,6 · 10-8 Grafito 3.500 · 10-8 Cobre 1,7 · 10-8 Baquelita 2·108-2·1011 Aluminio 2,6 · 10-8 Madeira 108 - 1011 Ferro 10 · 10-8 Vidro 1010 - 1014 Nichrome 100 · 10-8 Mica 1011 - 1015 Resistividade dalgúns materiais (Ω·m)
A resistencia eléctrica mídese en ohms (Ω) e a resistividade (ρ) en Ω·m. A resistencia pódese calcular matematicamente pola seguinte fórmula:
Exemplo: cálculo da resistencia dun fío de ferro de 0,1 mm2 de sección e 40 m de lonxitude.
Solución: cómpre expresarmos todos os datos en unidades do S.I.
s = 0,1 mm2 = 0,1 / 1.0002 m = 10-7 m2
Por outra parte, a resistividade do ferro é: ρ = 10 · 10-8 Ω·m
Xa que logo: R = ρ·l / s = 10 · 10-8 Ω·m · 40 m / 10-7 m2 = 40 Ω
As resistencias utilizadas nos circuítos eléctricos do mercado están provistas no exterior dunhas bandas de cores que indican o valor da súa resistencia eléctrica. O significado destas bandas de cores é o seguinte:
-
A primeira e a segunda indican as dúas primeiras cifras do valor da resistencia.
-
A terceira banda indica o número de ceros que cómpre engadir ás cifras anteriores.
-
A última derradeira infórmanos da tolerancia de fabricación ou precisión da resistencia, en forma de porcentaxe.
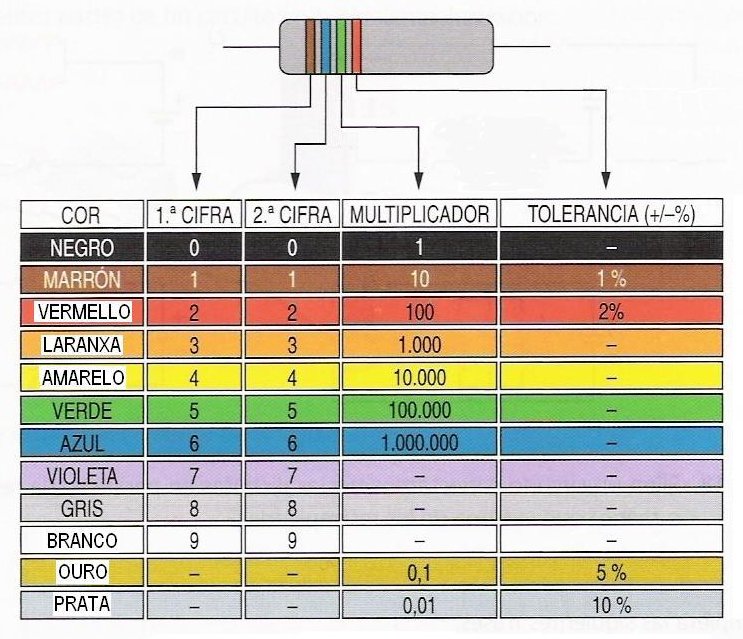
Por exemplo, na resistencia anterior as cores son marrón-azul-verde-vermello. A cor marrón indícanos que o primeiro díxito é un 1, e a cor azul que o segundo díxito é un 6. Como a terceira cor é verde haberá que engadir cinco ceros ás cifras anteriores. Por tanto, trátase dunha resistencia de 1.600.000 ohms. A cor vermella última significa que a tolerancia de fabricación é dun 2 %, é dicir, ± 32.000 ohms.
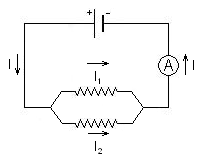
| Asociación de resistencias en serie | Asociación de resistencias en paralelo |
|
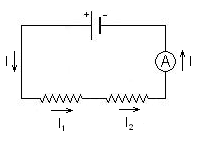
Varias resistencias están colocadas en serie cando por todas elas circula a mesma intensidade de corrente. A diferenza de potencial entre os extremos da asociación obtense sumando as diferenzas de potencial nos extremos de cada unha das resistencias. I = I1 = I2 A resistencia equivalente (Re) dunha asociación de resistencias dispostas en serie é a suma das resistencias (R1, R2). Re = R1 + R2 |
Varias resistencias están colocadas en paralelo ou derivación cando a intensidade total que circula pola asociación é a suma das intensidades que circulan por cada unha das resistencias. A diferenza de potencial entre os extremos de cada resistencia é a mesma. I = I1 + I2 A resistencia equivalente (Re) das resistencias dadas (R1, R2) calcúlase mediante a seguinte fórmula: Por tanto, para aumentar a resistencia dun circuíto colocaremos as resistencias en serie, e para diminuíla colocarémolas en paralelo. |
|
|
|
Lei de Ohm
A denominada lei de Ohm (científico alemán de comezos do século XIX) permítenos relacionar as tres magnitudes da corrente eléctrica estudadas ata agora: intensidade (I), diferenza de potencia ou voltaxe (V) e resistencia (R), e podémola enunciar así:
-
A intensidade da corrente eléctrica que circula por un condutor é directamente proporcional á diferenza de potencial aplicada entre os seus extremos e inversamente proporcional á súa resistencia.
Matematicamente pódese expresar por calquera das seguintes fórmulas:
Exemplo 1. Cálculo da resistencia dun receptor eléctrico polo que circula unha corrente de 0,1 amperes de intensidade cunha diferenza de potencial de 220 V.
Solución: R = V/I => R = 220 V / 0,1 A = 2.200 Ω
Exemplo 2. Cálculo da intensidade da corrente que circula por un condutor eléctrico de 45 Ω de resistencia baixo unha tensión de 9 V.
Solución: I = V/R => I = 9 V / 45 A = 0,2 A
Enerxía e potencia
Para que unha lámpada conectada nun circuíto eléctrico se acenda é preciso proporcionarlle enerxía. Esta é a función do xerador eléctrico. En virtude do principio de conservación da enerxía, podemos concluír que a enerxía eléctrica proporcionada ao circuíto polo xerador debe ser igual á consumida nel, que se converte noutras formas de enerxía.
A enerxía (W) consumida nun circuíto eléctrico pódese calcular en unidades do SI a partir da diferenza de potencial (V), da intensidade (I) e do tempo (s) mediante a seguinte expresión:
W = V · I · t
Lembrando que, segundo a lei de Ohm, V = R · I, e substituíndo esta expresión na fórmula anterior obtemos outra fórmula para a enerxía eléctrica:
W = R · I2 · t
A unidade de enerxía no SI é o joule (J).
A enerxía consumida nunha hora por unha lámpada pode ser igual á consumida por un radiador eléctrico en cinco minutos. Neste caso a enerxía é a mesma, pero o tempo que tarda en consumirse é distinto. A magnitude que relaciona a enerxía eléctrica e o tempo é a potencia eléctrica.
A potencia eléctrica (P) é a enerxía producida por un xerador, transferida ou consumida por un receptor na unidade de tempo. Xa que logo:
A unidade de enerxía eléctrica no SI é o watt (W) e o seu múltiplo o quilowatt (kW): 1 kW = 1.000 W
Despexando a enerxía eléctrica na fórmula da potencia: P = W / t, temos que:
W = P · t
Desta expresión obtemos outra unidade de enerxía moi utilizada que é o quilowatt hora (kWh). A equivalencia entre o kWh e o joule (ou watt · segundo) obtense transformando os quilowatts en watts e as horas en segundos:
1 kWh = 1 kW · h = 1.000 W · 3.600 s = 3.600.000 W·s = 3,6 · 106 J
|
|
|
Placa de características técnicas dun aparello eléctrico Potencia (110 W), tensión (230 V), intensidade que soporta (0,4 A) e frecuencia da corrente á que traballa (50 Hz). |
Efectos da corrente eléctrica (efecto Joule)
O paso da corrente eléctrica a través dun condutor produce varios efectos. Un deles é o efecto calorífico ou efecto Joule, que foi o primeiro científico en estudalo. Recibe o nome de efecto Joule o fenómeno polo que, ao pasar a corrente eléctrica por un condutor, unha parte da enerxía eléctrica se transforma en enerxía calorífica. Tendo en conta que un joule equivale a 0,24 calorías, e que a calor é un tipo de enerxía, podemos obter a calor (Q) producida nun aparello ao paso da corrente coa fórmula da enerxía:
Q = 0,24 · V · I · t
ou tamén:
Q = 0,24 · R · I2 · t
De acordo coas fórmulas anteriores, a calor producida é maior canto maiores sexan a voltaxe, a intensidade da corrente e a resistencia do aparello.
O efecto Joule ten moitas aplicacións. Por exemplo:
-
Fusibles. Serven para protexer os aparellos conectados en liña. Se un circuíto experimenta un aumento brusco da intensidade por unha subida da tensión ou un curtocircuíto, os aparellos conectados poden quecer ou estragarse. Para evitalo colócanse no circuíto uns fíos moi delgados chamados fusibles, que se funden ao atravesalos unha corrente de intensidade superior a aquela para a que foron calculados. Deste xeito interrómpese o paso da corrente e os aparellos conectados no circuíto quedan protexidos.
-
Aparellos eléctricos. As cociñas, os fornos, os quentadores eléctricos, os ferros de pasar, etc., funcionan transformando a enerxía eléctrica en calorífica, para o que incorporan un fío condutor de elevada resistencia que quece ao paso da corrente eléctrica.
-
Lámpadas incandescentes. Nelas a enerxía eléctrica transfórmase en enerxía luminosa e, en parte, en enerxía calorífica. Dispoñen dun filamento de volframio moi resistente colocado no interior dunha ampola de vidro na que se fixo o baleiro.
-
Menos de 0,01 A: imperceptible ou pequeno formigo.
-
0,02 A: dor, dificultade respiratoria e perda de coñecemento.
-
0,1 A: fallos na circulación do sangue.
-
Máis de 0,2 A: queimaduras graves, parada cardíaco e posible morte.


Efectos da corrente eléctrica no corpo humano Fusibles
Material que ao atravesalo unha corrente de intensidade superior á establecida, quece e fúndese
James P. Joule (1818-1889)
Físico inglés que investigou a produción de calor pola corrente eléctrica
-
Actividades resoltas
Vexamos como utilizar a lei de Ohm para calcular magnitudes da corrente eléctrica.
-
-
O valor dunha resistencia pola que circula unha corrente de 0,25 A de intensidade cando o voltímetro marca 8 V
As fórmulas que nos serven para relacionar estas tres magnitudes son as da lei de Ohm. Neste caso deberemos calcular a resistencia (R) coñecendo a intensidade (0,25 A) e a diferenza de potencial (8 V):
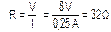
-
A diferenza de potencial nos extremos dunha lámpada de 40 Ω de resistencia pola que circula unha corrente de 0,6 A de intensidade
Para calcular a diferenza de potencial (V) coñecendo a resistencia (40 Ω) e a intensidade (0,6 A), utilizaremos outra fórmula procedente da lei de Ohm:
V = I · R = 0,6 A · 40 Ω = 24 V
-
Sabendo que por un forno eléctrico conectado a unha rede de 220 V circula unha corrente de 10 A de intensidade, calcular:
-
-
A potencia eléctrica do forno
A fórmula para o cálculo da potencia eléctrica (P) a partir da diferenza de potencial (V) e da intensidade (I) é a seguinte: P = V · I. Polo tanto:
P = V · I = 220 V · 10 A = 2 200 W
-
A súa resistencia
A resistencia pódese calcular utilizando a lei de Ohm:
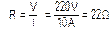
-
Actividades propostas
S5. En que se diferencian a corrente continua e a corrente alterna? A cal destes tipos pertence a corrente doméstica?
S6. Por que os circuítos domésticos adoitan ter os aparellos conectados en paralelo?
S7. Investigue que son os semicondutores e que aplicacións teñen.
S8. Debuxe un circuíto que conteña os seguintes elementos: unha pila, un interruptor, dúas resistencias en serie, un amperímetro que mida a intensidade que circula por todo o circuíto e dous voltímetros que midan a diferenza de potencial en cada resistencia.
S9. Como inflúen a lonxitude e a sección na resistencia eléctrica dun condutor?
S10. A lonxitude dun fío condutor de aluminio é de 5 m e ten unha sección de 6 mm2. Que resistencia ofrecerá ao paso da corrente? (A resistividade do aluminio é a seguinte: ρ = 2,6 · 10-8 Ω·m).
S11. Calcule o valor das seguintes resistencias sabendo que as súas cores son:
| Laranxa, marrón, amarelo | Negro, violeta, vermello | Verde, gris, azul | Azul , vermello, prata |
S12. Temos tres resistencias de 4, 6 e 8 Ω, respectivamente. Calcule a resistencia total do conxunto en cada un dos seguintes casos:
|
Se se conectan en serie |
Se se conectan en paralelo |
Primeiras en serie e 3ª en paralelo |
S13. A resistencia total dun conxunto de dúas resistencias conectadas en paralelo é de 6 Ω. Se unha das resistencias vale 10 Ω, cal é o valor da outra?
S14. Un torrador de pan de 660 W de potencia está conectado a unha de rede de 220 V. Calcule:
- A intensidade da corrente que circula a través del
- A súa resistencia
S15. Por un televisor conectado a unha rede de 220 V circula unha corrente de 0,8 A.
- Ache a súa potencia eléctrica, e exprese o resultado en watts e en quilowatts.
- A enerxía que consume en tres horas de funcionamento e o seu custo, supondo que o prezo do kWh é de 0,12 euros
S16. Por un termo eléctrico de 25 Ω de resistencia pasa unha corrente de 150 V.
- Calcule a súa potencia eléctrica.
- Ache calor desprendida en dúas horas de funcionamento.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0