2.5 Función de proporcionalidade inversa
Se hai que facer un determinado traballo, canto maior sexa a potencia menor será o tempo que se tarda en facelo, como xa sabemos. Podemos concretar un pouco máis: se a potencia é o dobre, o tempo empregado será a metade; se a potencia é o triplo, o tempo será tres veces menor, e así sucesivamente. Cando ocorre isto, dicimos que esas dúas magnitudes son inversamente proporcionais.
- Exemplo 1. Hai que facer un traballo de 10 000 J. Canto tempo tardaremos en facelo? Depende da potencia que utilicemos; imos facer unha táboa tempo/potencia (despexamos o tempo da fórmula da potencia: P = W/t → t = W/P)
-
Potencia ( W) Tempo (s) [t=WP]
10
100
200
400
1000
1000
100
50
25
10
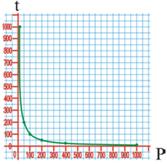
Relacións deste tipo entre dúas magnitudes son frecuentes en ciencias e na vida cotiá. Matematicamente podemos escribilas de forma xeral coa expresión
![]()
onde k é un número fixo que se chama constante de proporcionalidade.
En xeral, a variable x pode tomar tamén valores negativos. Fíxese que da expresión anterior da función dedúcese que o produto das dúas variables dá sempre o mesmo resultado:![]()
- Exemplo 2. Representamos graficamente a función y = 4/x. Facemos primeiro unha táboa de valores x - y e logo representamos.
-
X Y -4
-2
-1
1
2
4
-1
-2
-4
4
2
1
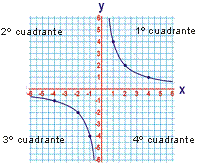
A representación gráfica é unha curva que se chama hipérbole. Ten dúas ramas que, neste caso, están no primeiro e no terceiro cuadrante dos eixes coordenados. Observe que a curva non corta os eixes nin tampouco pasa pola orixe de coordenadas; as dúas ramas pódense achegar moito aos eixes, pero sen tocalos: estes son rectas asíntotas.
Unha recta é asíntota a unha curva cando esta se achega indefinidamente á recta pero sen tocala nunca. Se a constante k de proporcionalidade é positiva, como na función anterior, a función é decrecente: ao aumentar x diminúe y. Se vostede vai seguindo a curva de esquerda a dereita verá que “vai baixando”, é decrecente.
Vexamos como é a gráfica no caso de ser k negativa. Sexa a función y = -4/x:
-
X Y -4
1

-2
2
-1
4
1
-4
2
-2
4
-1
Xa ve que se k é negativa as dúas ramas da hipérbole están nos cuadrantes 2º e 4º, e que a función é sempre crecente. En todos os casos, a gráfica é simétrica respecto da orixe de coordenadas: a cada punto de coordenadas (x, y) correspóndelle outro simétrico de coordenadas (-x, -y). Se a gráfica pasa polo punto (3, -6) daquela tamén pasa polo (-3, 6).
S28. Represente graficamente as funcións de proporcionalidade inversa seguintes:
-
- y = 6/x
- x.y = -1 (terá que despexar y)
S29. Catro amigos dobran as portadas duns CD; van tardar 50 minutos. Canto tardarían se lles axudasen dúas amigas máis? E se un tivese que marchar.
S30. Dúas cintas transportadoras de maletas precisan 30 minutos para cargalas nun avión. Canto tardarían cinco cintas? E unha soa cinta?
S31. Determine se a táboa de datos corresponde a unha función de proporcionalidade inversa (os datos corresponden ao número de operarios que fan unha obra):
| X | Y |
| 100 | 10 |
| 200 | 5 |
| 300 | 3 |
| 400 | 2 |
| 500 | 1 |
S32. Nunha granxa hai 60 vacas. Teñen pasto para alimentalas durante 20 días. Se venden dez vacas e morren cinco, cantos días poderán comer as vacas que quedan?
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0