2.3.1 Conservación da enerxía mecánica

Vimos nesta unidade que a enerxía se conserva constante no universo. Este é un principio fundamental na física: non se coñece ningún proceso en que non se cumpra.

Principio de conservación da enerxía mecánica

Hai un caso particular deste principio de conservación, chamado principio de conservación da enerxía mecánica, pero só é verdadeiro baixo certas condicións. Este principio establece que se as únicas forzas que fan traballo sobre un corpo son a gravitacional, a elástica e a electrostática, daquela a enerxía mecánica do corpo é a mesma en todos os puntos da súa traxectoria: a enerxía mecánica consérvase constante.

Dous casos frecuentes en que non se conserva a enerxía mecánica son cando hai rozamento ou cando hai forzas de tracción (motores, tensión de cables, as forzas que facemos co noso corpo…) Neste caso o traballo feito por estas forzas invístese en variar a enerxía mecánica:

Sendo W_n o traballo feito polas forzas que non son nin o peso nin as elásticas (nin as electrostáticas). Daquela, o traballo feito polo motor dun coche vai parar en aumentar a enerxía mecánica do coche; o traballo feito polo rozamento sempre diminúe a enerxía mecánica dos corpos, e acaba transformándose en calor.

Actividades resoltas

Deixamos caer unha pedra de 2 kg desde unha altura de 100 m, supondo nulo o rozamento contra o aire. Calculamos:

• • O valor da enerxía cinética, potencial e mecánica no punto inicial do percorrido.

Solución

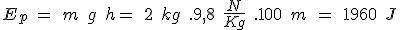
No inicio do percorrido non se move, non ten enerxía cinética. Pero si que ten enerxía potencial gravitacional:   Xa que logo, a enerxía mecánica no punto inicial é E = Ec + Ep = 0 + 1960 J = 1 960 J.

• • O valor da enerxía mecánica cando está a 30 m de altura sobre o chan.

    Solución

    Calculemos a velocidade do corpo cando está a 30 m de altura sobre o chan. Leva percorridos 70 m; a velocidade nese intre é:   polo que a súa enerxía cinética é: , entanto que a enerxía potencial a esa altura é: 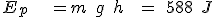. A enerxía mecánica resulta ser: 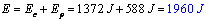, o mesmo valor que tiña no punto inicial.

  • A enerxía mecánica cando está xusto a piques de bater contra o chan.

Solución

Cando xusto chega ao chan, a altura é cero e non ten enerxía potencial; a velocidade coa que chega o corpo é: e a enerxía total resulta ser .

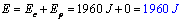Xa que logo, a enerxía mecánica vale o mesmo nos tres puntos do percorrido. A enerxía potencial gravitacional vai diminuíndo ao tempo que aumenta a enerxía cinética do corpo, de xeito que a súa suma (a enerxía mecánica) non cambia.

O principio de conservación, cando se pode aplicar, permite resolver moitos exercicios de dinámica, aparentemente complicados, dun xeito bastante fácil, como é este caso:

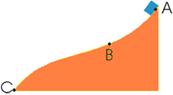
Un bloque de 4 kg lánzase ao longo dunha costa ondulada sen rozamento cunha velocidade inicial de 4 m/s. Calculamos a velocidade con que pasará polos puntos B e C do percorrido [altura do punto A = 10 m; altura do punto B = 6 m; o punto C está no chan].

Solución

Resolver este exercicio usando as ecuacións da dinámica de Newton é moi difícil debido á ondulación da costa. As forzas que actúan sobre o corpo no percorrido son o peso e a forza normal. Pero esta última non fai traballo, por ser sempre perpendicular á traxectoria (aínda que non sexa recta); a única forza que traballa é o peso, e polo tanto cúmprese o principio de conservación da enerxía mecánica en todo o percorrido. A enerxía mecánica do corpo é a mesma nos puntos A, B e C. No punto inicial, a súa enerxía mecánica é:

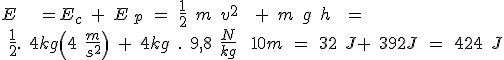
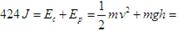
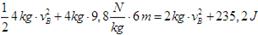
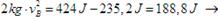
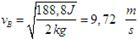
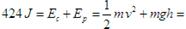
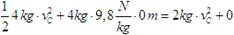
No punto intermedio B, a enerxía mecánica ten que seguir valendo o mesmo, 424 J. Daquela: Despexando a velocidade:   E o mesmo ocorre no punto C, a enerxía mecánica tamén segue valendo 424 J, e resolvemos do mesmo xeito:   (no punto C a altura é cero e polo tanto a enerxía potencial tamén é cero). Despexando a velocidade:

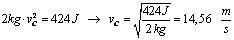
Un coche de 1000 kg vai a 72 km/h por unha estrada horizontal cun coeficiente de rozamento 0,3. O automóbil ponse en punto morto. Cantos metros percorrerá ata parar?

Solución

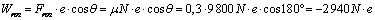
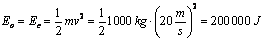
Non se conserva a enerxía mecánica, xa que o rozamento fai traballo neste caso. Comecemos calculando o traballo feito polo rozamento:   sendo e o espazo percorrido polo automóbil, tendo en conta que cos 180º = -1 e que a forza normal é igual ao peso neste caso. A enerxía mecánica inicial do coche é só cinética (non ten potencial porque h = 0), e vale:   No intre final, cando o coche quede finalmente parado, non ten enerxía mecánica, xa que a cinética é cero e a potencial segue sendo cero. 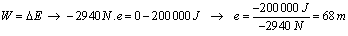Xa que logo,   O coche parará logo de percorrer 68 metros. Onde foi parar a enerxía que tiña o coche inicialmente? En calor nas rodas, no asfalto e, un pouco, no aire e no propio coche.