Para situar los puntos en un mapa, o en el plano cartesiano, necesitamos indicar a partir de un punto (en nuestro caso el origen de coordenadas) cuánto nos hemos movido a izquierda o derecha y arriba o abajo.

Así cada punto quedará determinado por esas dos características, ese par de números se denomina coordenadas del punto: (abscisa, ordenada).

Las coordenadas de un punto \(P\) son el par ordenado de números \((x, y)\):

la primera coordenada, \(x\) es la coordenada de la abscisa y nos indica a qué distancia del eje vertical se encuentra el punto.

la segunda coordenada, \(y\), es la ordenada, e indica la distancia del punto al eje horizontal.

Cuando en el eje horizontal, en las abscisas, nos movemos a la izquierda del origen, las coordenadas de los puntos serán negativas. Lo mismo sucede con la ordenada cuando estamos por debajo de origen.

Si un punto se encuentra sobre el eje de abscisas, su ordenada será \(0\), será de la forma \((x, 0)\). Y en caso de estar sobre el eje de ordenadas, será \(0\) la coordenada de la abscisa, \((0, y)\).

Observa las coordenadas de los siguiente puntos:

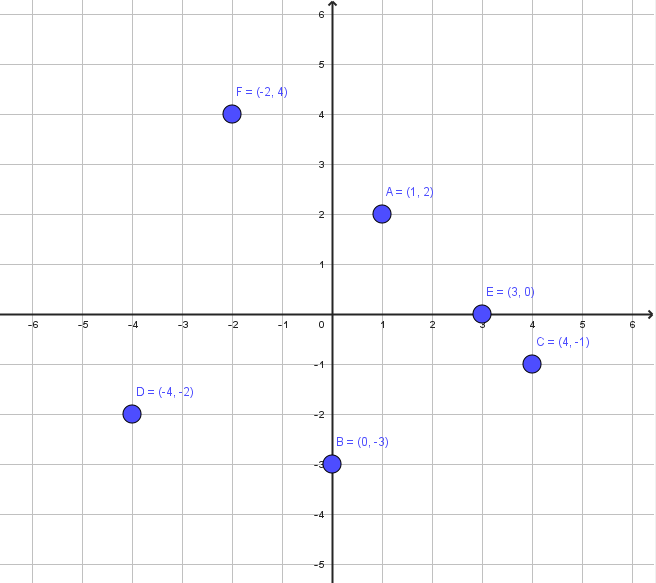
El punto A tiene de coordenadas (1, 2). Como ambas son positivas el punto está en el primer cuadrante.

B tiene de coordenadas (0, -3). Como la coordenada de la abscisa es cero, el punto está sobre el eje de ordenadas o eje de las Y.

El punto C tiene de coordenadas (4, -1). La abscisa es positiva y la ordenada es negativa, el punto se encuentra en el cuarto cuadrante.

D tiene de coordenadas (-4, -2). Ambas coordenadas son negativas, el punto está en el tercer cuadrante.

El punto E está sobre el eje de abscisas porque la coordenada de la y es cero. Sus coordenadas son (3, 0).

En el segundo cuadrante está el punto F, ya que su abscisa es negativa y su ordenada positiva. Las coordenadas de este punto son (-2, 4).