6.1 Solucións das actividades propostas
S1.
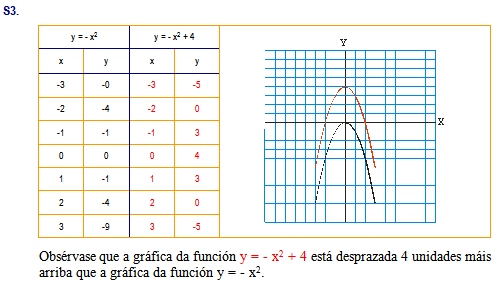
|
a = -3/2 < 0 Cóncava |
|
|
a = 7 > 0 Convexa |
|
a = 3/5 > 0 Convexa |
|
a = - 0,32 < 0 Cóncava |


S6.
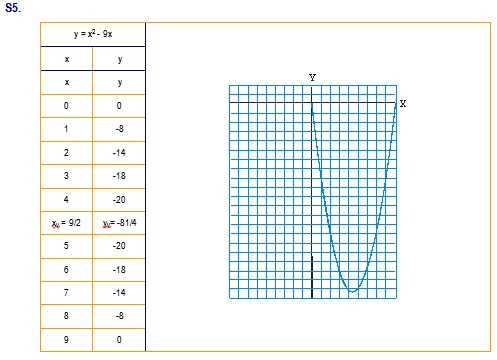
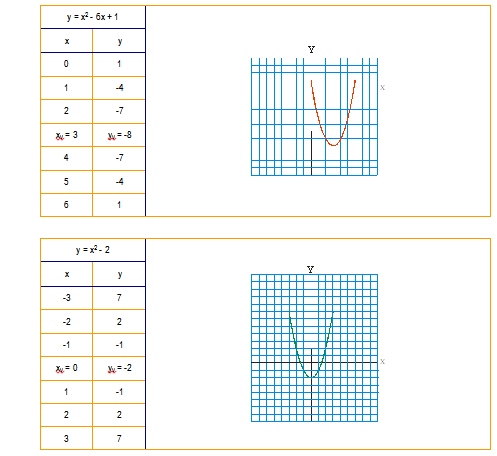
|
a > 0 , b < 0 a, b teñen distinto signo. O vértice está situado á dereita. |
|
|
a > 0 , b < 0 a, b teñen distinto signo. O vértice está situado á dereita. |
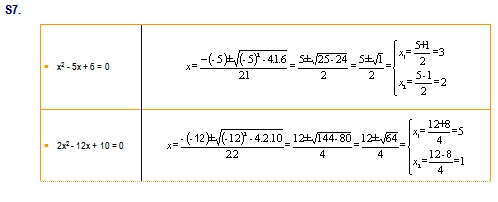
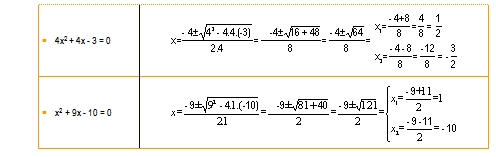
S8.
|
b2 - 4ac = (-6)2 – 4.3.3 = 36 – 36 = 0 → A ecuación ten unha solución |
|
b2 - 4ac = 12 – 4.1.(-3) = 1 + 12 = 13 > 0 → A ecuación ten dúas solucións |
|
b2 - 4ac = 12 – 4.1.3 = 1 - 12 = -11 < 0 → A ecuación non ten solución |
|
b2 - 4ac = (-2)2 – 4.(-1).(-3) = 4 - 12 = -8 < 0 → A ecuación non ten solución |
|
b2 - 4ac = 52 – 4.2.1 = 25 - 8 = 17 > 0 → A ecuación ten dúas solucións |



S12.
|
Sexa x a idade da persoa. O seu cadrado será x2, o triplo será 3x e nove veces esta, 9x. Segundo as condicións do problema escribimos a ecuación: x2 – 3x = 9x Agrupamos no primeiro membro e reducimos: x2 – 3x – 9x = 0 → x2 -12x = 0 Ao tratarse dunha ecuación de segundo grao sen termo independente, podemos descompoñer en factores extraendo x factor común: x(x -12) = 0 As solucións son: x1 = 0 x – 12 = 0 → x2 = 12 Comprobación: x1 = 0 → 02 – 3·0 = 9·0 → 0 – 0 = 0 (solución trivial) x2 = 12 → 122 – 3·12 = 9·12 → 144 – 36 = 108 → 108 = 108 |






S19
S20.






Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0