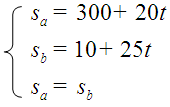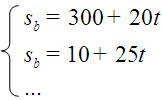2.3.2 Resolución de problemas mediante sistemas de ecuacións
Resolvamos agora o problema da moto que alcanza ao coche. As ecuacións eran:
Despexamos sa da terceira ecuación (de feito xa está despexada) e substituímos o seu valor nas outras dúas ecuacións:
Resolvemos polo método de igualación, despexando nas dúas ecuacións sb (en realidade xa están despexadas):
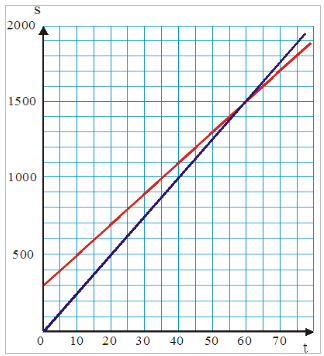
e sb = 300 + 20.t = 300 + 20.58 = 1.460 metros.
Graficamente:
-
sa = 300 + 20.t
sb = 10 + 25.t
t
sa
t
sb
0
300
0
10
20
700
20
510
40
1100
40
1010
60
1500
60
1510
80
1900
80
2010
S21. Ache dous números que sumen 84 e que o seu cociente sexa 6.
S22. Nun curral hai galiñas e coellos; hai 50 cabezas e 134 patas. Cantos coellos e cantas galiñas hai?
S23. O produto de dous números é 4 e a suma dos seus cadrados é 17. Cales son os números?
S24. Temos dous tipos de pensos, un de 0,50 euros o quilogramo e outro de 0,80 euros o quilogramo. Que cantidade de cada tipo debemos mesturar para termos 100 kg de penso a 0,704 euros cada quilogramo?
S25. Unha persoa percorre 1 000 km, parte en coche e parte en bicicleta. No coche vai a 90 km/h e na bicicleta a 20 km/h. Tardou 15 horas en completar a viaxe. Cantos quilómetros fixo en bicicleta?
S26. Un hotel ten cuartos dobres e individuais; en total son 120 cuartos. O número de camas é 195. Cantos dos cuartos son dobres?
S27. Nunha festa, se cada invitado come cinco pasteis daquela sobran tres, e se come seis falta un. Cantos invitados e cantos pasteis hai na festa?
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0