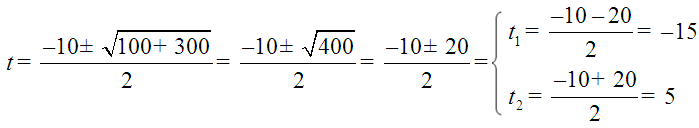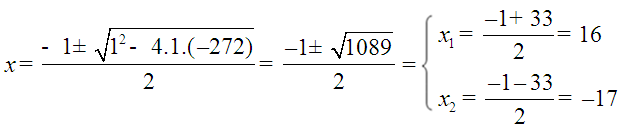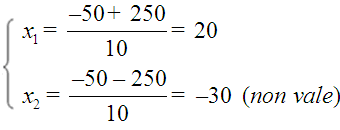2.2.5 Resolución de problemas utilizando ecuacións de segundo grao
Por fin podemos resolver xa o problema co que iniciamos esta sección: cando pasará o móbil pola posición s = 78 m? (vaia atrás e léao novamente).
Solución:
Resolvendo a ecuación:
A primeira solución (t = - 15 s) non ten sentido físico, ao non existiren tempos negativos, así que a rexeitamos. A solución válida é que aos 5 s o móbil pasará pola posición 78 m.
As ecuacións de segundo grao permiten resolver problemas de móbiles e de moitos outros campos da ciencia e da vida cotiá. Vexamos uns cantos.
-
Exemplo. Desde unha altura de 100 m lanzamos verticalmente cara abaixo un corpo cunha velocidade inicial de 10 m/s. Canto tempo tarda en chegar ao chan?
-
Solución: o movemento é uniformemente acelerado, usamos a ecuación da posición:
-
Exemplo. O produto dun número natural polo seguinte é 272. Cal é ese número?
-
Solución: sexa x o número buscado. Daquela x(x+1) = 272; facendo as operacións temos:
Resolvendo:
O número natural buscado é 16. A solución x2 = -17 é dun número enteiro.
-
Exemplo. Nun cadrado a área é igual ao dobre do perímetro. Cando mide o lado do cadrado?
-
- Solución: sexa x a lonxitude do lado do cadrado.
Área = x2; Perímetro = x + x + x + x = 4x
Condición do problema: área = 2.perímetro → x2 = 2.4x;
É unha ecuación incompleta.
O lado do cadrado mide 8.
-
Exemplo. Un almacén mercou un lote de caixas e pagou por todas elas 300 euros. Cos mesmos cartos podería comprar dez caixas máis se cada unha custase 5 euros menos. Cantas caixas mercou?
-
Solución: sexa x o número de caixas. O prezo de cada caixa é
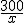
Condición do problema:
Facendo as operacións:
Resolvendo a ecuación de segundo grao:
Comprou 20 caixas a 15 euros cada unha.
S10. Reparta o número 10 en dous sumandos de xeito que a suma dos seus cadrados sexa 50.
S11. Se ao triplo dun número se lle suma o seu cadrado obtense 88. Cal é o número?
S12. Ache a idade dunha persoa sabendo que se ao seu cadrado se lle resta o triplo da idade resulta nove veces esta.
S13. Un rectángulo ten 24 m de perímetro e 35 m2 de área. Ache as dimensións do rectángulo.
S14. Determine o perímetro dun triángulo rectángulo isóscele cuxa área é 12 m2.
S15. Un campo de fútbol mide 30 m máis de longo que de ancho; a súa área é de 7.000 m2. Canto miden os lados do campo?
S16. Dous números diferéncianse en sete unidades, e o seu produto é 60. Cales son eses números?
S17. Nun triángulo rectángulo de 24 m de perímetro, a lonxitude dun cateto é igual aos 3/4 do outro. Determine as dimensións do triángulo.
S18. O Instituto regala 525 euros para os repartir entre o alumnado de ESA. Como 25 alumnos non asisten hoxe á clase, cada un dos presentes obtivo 0,50 euros máis. Cantos alumnos hai en total en ESA?
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0