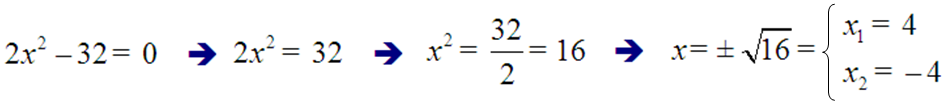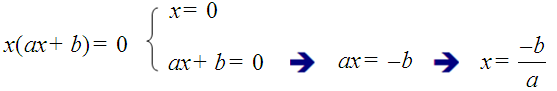2.2.3 Ecuacións de segundo grao incompletas

Son as ecuacións nas que os termos b ou c valen 0.

Ecuacións de tipo ax² + c = 0

Son o caso no que b = 0. O método máis sinxelo de resolución é despexar a incógnita x:

Se o valor de

é positivo a raíz pódese efectuar e a ecuación ten dúas solucións, pero se o cociente é negativo, a raíz non existe e a ecuación non ten ningunha solución real.

• Exemplo. Resolver a ecuación 2x² - 32 = 0.

• Exemplo. Resolver a ecuación x² + 1 = 0.

......Non ten solución real.

 

 

Ecuacións de tipo ax² + bx = 0

 

Son o caso cando c = 0. O máis sinxelo é sacar factor común x:

 

ax² + bx = 0 → x (ax + b) = 0

 

Temos a multiplicación de dous factores, x e (ax + b). A única forma de que multiplicando dous factores sexa cero é que un deles, ou os dous, sexan nulos:

 

 

Polo tanto este tipo de ecuacións incompletas sempre ten dúas solucións, unha delas x = 0.

 

• Exemplo. Resolver a ecuación 5x² - 125x = 0.