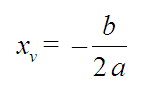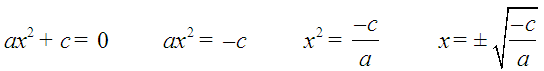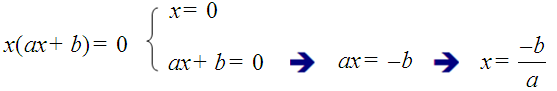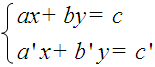3. Resumo de contidos

A función cuadrática

• As funcións cuadráticas son as que se poden expresar mediante un polinomio de segundo grao da forma y = ax² + bx + c (con a ≠ 0), e a súa gráfica sempre é unha parábola.

• Características das gráficas das funcións cuadráticas:

• A gráfica alcanza o seu punto máximo ou mínimo no vértice da parábola. A coordenada x_v do vértice obtense mediante a fórmula:

• A gráfica é simétrica respecto dun paralelo ao eixe OY, e ten dúas pólas: nunha póla a función é crecente e na outra é decrecente.

• A gráfica pode ser cóncava (aberta cara abaixo Λ), se a < 0, ou convexa (aberta cara arriba V), se a > 0.

• A ecuación de segundo grao

  • Unha ecuación de segundo grao ax² + bx + c = 0 é completa cando os coeficientes a, b e c son todos distintos de cero. Se os coeficientes b ou c, ou os dous, son nulos, a ecuación chámase incompleta.

  • As solucións da ecuación de segundo grao obtéñense a partir da expresión:

Número de solucións dunha ecuación de segundo grao

• O número de solucións dunha ecuación de segundo grao depende do valor do seu discriminante. O discriminante é o termo: b² - 4ac.

• Existen tres posibilidades, segundo o signo do discriminante:

• Discriminante b² - 4ac > 0 → A ecuación ten dúas solucións distintas.

• Discriminante b² - 4ac = 0 → A ecuación ten unha solución (solución dobre).

• Discriminante b² - 4ac < 0 → A ecuación non ten ningunha solución.

Ecuacións de segundo grao incompletas

Pódense resolver aplicando a fórmula xeral, substituíndo por 0 os coeficientes que faltan na ecuación, pero tamén se poden resolver despexando x directamente.

• Ecuacións de tipo ax² + c = 0

Despexamos directamente a incógnita x:

• Ecuacións de tipo ax² + bx = 0

Sacamos factor común x e igualamos a cero os dous factores:

ax² + bx = 0 → x (ax + b) = 0

Este tipo de ecuacións sempre ten dúas solucións, unha delas x = 0.

Solucións dunha ecuación e puntos de corte co eixe OX

• Os puntos de corte da gráfica da función cuadrática y = ax² + bc + c obtéñense resolvendo a ecuación ax² + bc + c = 0. Se as solucións da ecuación son x₁e x₂, os puntos de corte co eixe OX son os puntos de coordenadas (x₁, 0), (x₂, 0).

Sistemas de ecuacións lineais

• Unha ecuación é lineal cando é de primeiro respecto de todas as incógnitas, e non hai produtos nin divisións entre elas; por exemplo, 3x + 2y - 8 = 0.

• Un sistema de dúas ecuacións lineais con dúas incógnitas ten a forma xeral:

Métodos de resolución de sistemas de ecuacións lineais

• Existen catro métodos de resolución de sistemas de ecuacións lineais:

• Método de substitución: Despexamos unha incógnita, xeralmente a que resulte máis sinxela de despexar, e substituímos o seu valor na outra ecuación.

• Método de igualación: Despexamos a mesma incógnita nas dúas ecuacións e igualamos as expresións obtidas.

• Método de redución: Multiplicamos as ecuacións polos números convenientes de xeito que os valores dos coeficientes dunhas das incógnitas sexan opostos e, seguidamente, sumamos ambas ecuacións.

• Método gráfico: Despexamos a incógnita y en cada ecuación e representamos graficamente as funcións lineais obtidas, que serán dúas rectas. As coordenadas do punto de corte das rectas (x, y) serán as solucións do sistema.

Interpretación gráfica da solución dun sistema de ecuación lineais

• Segundo a posición relativa das rectas correspondentes ás ecuacións lineais que forman o sistema dado, poden existir tres posibilidades:

• As rectas córtanse nun punto (x, y): O sistema é compatible e ten solución e esta vén dada polos valores de x e y.

• As rectas son coincidentes: teñen infinitos puntos comúns. O sistema é compatible e ten infinitas solucións, que son os valores dos puntos (x, y) que pertencen á recta.

• • As rectas son paralelas. O sistema é incompatible xa que as rectas non teñen ningún punto común.