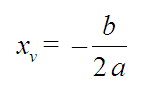2.1.3 Gráfica da función cuadrática completa y = ax2 + bx + c
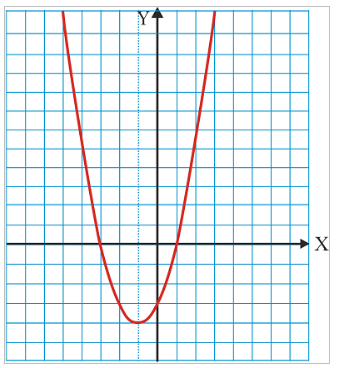
Representemos graficamente a seguinte parábola: y = x2 + 2x - 3:
-
y = x2 + 2x - 3
x
y
- 3
0
- 2
- 3
- 1
- 4
0
-3
1
0
2
5
3
12
Como a > 0, a parábola é convexa (aberta cara a arriba).
Pode demostrarse que, para calquera parábola, a coordenada x do vértice vén dada pola expresión:
Isto quere dicir que se a e b teñen o mesmo signo, o eixe de simetría da parábola e o vértice estarán desprazados cara á esquerda do eixe OY (como no exemplo anterior), e se teñen signos contrarios estarán desprazados cara á dereita. O parámetro c xoga o mesmo papel de subir ou baixar a gráfica que xa vimos antes.
Para representarmos unha parábola convén calcularmos primeiro a posición do seu vértice, e logo completar a táboa de valores x-y dándolle a x valores simétricos respecto de xv.
S4. Calcule as coordenadas do vértice das parábolas:
|
y = x2 - 8 |
y = x2- x + 5 |
y = 1/2 x2 - 4x + 1 |
y = - x2 - 2x + 4 |
y = 3x2 + 6x - 1 |
S5. Represente graficamente as funcións cuadráticas seguintes: y = x2 - 9x;
y = x2 - 6x + 1; y = x2 – 2.
S6. Sen debuxar a gráfica, determine se o eixe de simetría e o vértice das parábolas están á esquerda ou á dereita do eixe OY: y = x2- 3x + 5; y = x2 - 4x.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0